14. Пропорция - математика архитектурной гармонии

Гармония - вот что лежит в основе всех видов искусства на всем протяжении человеческой истории.

И. Жолтовский

Ты ползал вокруг могучих развалин, чтобы вымолить у них тайну пропорции.

И. В. Гёте

Церковь Покрова Богородицы на Hep ли. 1165. Весенним половодьем церковь плывет над водой, будто сказочное видение

Весенним половодьем белым видением из сказочного града Китежа встает над водой, залившей луга, церковь Покрова Богородицы... "Сей же великий князь Андрей, аще печалию о скончавшемся сыне объят быв, и скорбяше, обаче более в богоугодныя дела поощряшеся... на реке Клязьме, в лугу, нача здати церковь во имя Пресвятыя Богородицы Честнаго ея Покрова, на устьи реки Нерли... и помо-щию Пресвятыя Богоматере оную церковь единым летом соверши",- сказано в житии великого князя Андрея Боголюбского о постройке храма в лето 1165. Более восьмисот раз разливалась с тех пор тихая Нерль, и кажется, будто церковь Покрова родилась вместе с речкой, ее лугами и перелесками, а не стоит на искусственном холме, на мощном десятиметровом фундаменте, созданном руками человека... В чем красота и очарование церкви Покрова на Нерли? Ведь она имеет скромные размеры (высота от основания до маковки - 24 м), ее архитектурные формы крайне просты, а белокаменные украшения сдержаны и лаконичны. И тем не менее церковь по праву считается жемчужиной русской архитектуры. Почему?

Ответить на этот вопрос лучше всего словами выдающегося советского зодчего, автора гостиницы "Москва", Казанского вокзала, академика А. В. Щусева (1873- 1949): "Пожалуй, самым трудным и вместе с тем обязательным в архитектурном творчестве является простота. Простота форм обязывает придавать прекрасные пропорции и соотношения, которые сообщили бы им необходимую гармонию".

Но и за 300 лет до Щусева представитель другой эпохи и другого архитектурного направления, французский зодчий Франсуа Блондель (1618-1686) в своем "Курсе архитектуры" восторженно писал о пропорциях: "Удовлетворение, которое мы испытываем, глядя на прекрасное произведение искусства, проистекает оттого, что в нем соблюдены правила и мера, ибо удовольствие в нас вызывают единственно лишь пропорции. Если же они отсутствуют, то, сколько бы мы ни украшали здание, эти наружные украшения не заменят нам внутреннюю красоту и привлекательность, коль скоро их нет, и, пожалуй, можно сказать, что уродство становится еще ненавистнее и невыносимее, чем пышнее наружные украшения, чем дороже или роскошнее материал... Дабы подкрепить наше утверждение, я заявляю, что красота, возникающая из меры и пропорции, вовсе не требует дорогих материалов и изящной работы, дабы вызвать восхищение, напротив, она сверкает и делается все ощутимее, проступая сквозь грязь и хаос материала и его обработки. Нам приятно смотреть на некоторые соотношения тех готических зданий, красота которых, очевидно, возникла из симметрии и пропорций между целым и частями и внутри отдельных частей, и видна, невзирая на уродливые трещины и скрывающие их украшения".

Огромную роль пропорций прекрасно осознавали древнегреческие и древнеегипетские зодчие. Более того, по мнению другого французского архитектора и теоретика Виолле-ле-Дюка (1814 - 1879), "большое достоинство греческих зодчих состояло в том, что у них были выработаны законы пропорциональности в архитектуре и что греки им подчинялись, несчастье нашего времени составляет убеждение, что архитектурное произведение может быть создано, руководствуясь одним лишь воображением, одной лишь фантазией, подчиняясь единственно так называемому вкусу, одним словом так, как создается туалет красивой женщины".

В чем же заключается сила архитектурных пропорций? В том, что архитектурные пропорции - это математика зодчего. А математика - это универсальный язык науки (см. с. 40), поэтому мы можем сказать, что пропорции - это универсальный язык архитектуры, язык всеобъемлющий и всесильный, как всеобъемлюща и всесильна математика. Обратим внимание на то, что не случайно в высказываниях архитекторов о пропорциях так часто встречаются слова "внутренняя красота", "простота", "всеобщность", т. е. те же слова, которыми в главе 2 мы описывали качества математики.

Уже Платон глубоко понимал не только математическую, но и эстетическую сущность пропорции, позволяющей связывать целое и его части. Об этом свидетельствует следующий отрывок из цитированного нами "Тимея": "Невозможно, чтобы две вещи совершенным образом соединились без третьей, так как между ними должна появиться связь, которая скрепила бы их. Это наилучшим образом может выполнить пропорция, ибо если три числа обладают тем свойством, что среднее так относится к меньшему, как большее к среднему, и, наоборот, меньшее так относится к среднему, как среднее к большему, то последнее и первое и будет средним, а среднее первым и последним".

Этот отрывок, как и все у Платона, не сразу поддается пониманию. Однако он станет совершенно прозрачным, если его перевести на язык математики. Вводя обозначения: а - большее ("последнее") число, х - среднее число ("связь"), у - меньшее ("первое") число,- имеем х:у = =а:x, или у:х = х: а, или ау = х². С легкой руки Луки Пачоли (см. с. 209) считалось, что под х и у Платон понимал части целого а, т. е. что х + у = а, и поэтому Платон говорил о золотой пропорции (12.1) а:х = х:(а - х). Отсюда пошло мнение, что античные пропорции основаны на золотом сечении. Однако, как считает сегодня архитектор И. Ш. Шевелев, такое мнение не обосновано и речь у Платона идет о геометрической пропорции общего вида а:х = х:у, откуда следует совершенно иная теория античных пропорций (см. гл. 16).

Пропорции являются важным и надежным средством зодчего для достижения хрупкого и тонко сбалансированного равновесия между целым и его частями, имя которому - гармония. Напомним, что по сравнению с композитором или скульптором архитектор находится в более сложном положении, ибо на пути к гармонии он должен заботиться не только о "красоте", но также и о "пользе", и "прочности". Еще Гораций в послании к братьям Пизонам "Наука поэзии" в образной форме говорил о том, как непросто красиво и целесообразно соединять части в единое целое, что взятые вместе "части": лицо женщины, грива льва, тигровая шкура или павлиний хвост, которые сами по себе являются своеобразными эталонами красоты,- не только не дают нам прекрасного "целого"- гармонии, но представляют, по крайней мере, странное зрелище.

Если художник решит приписать к голове человечьей 
Шею коня, а потом облечет в разноцветные перья 
Тело, которое он соберет по куску отовсюду - 
Лик от красавицы девы, а хвост от чешуйчатой рыбы, - 
Кто бы, по-вашему, мог, поглядев, удержаться от смеха? 

Гармония в природе и гармония в архитектуре - две стороны единого великого процесса созидания. Замечательный советский зодчий и теоретик И. В. Жолтовский (1867-1959) считал творчество архитектора частью творчества природы. Широко известно высказывание Жолтовского о том, что архитектор - "дитя природы", что архитектурные формы должны члениться, следовать одна за другой, вырастать друг из друга, как ветви древесного ствола. Впрочем, ту же мысль на 500 лет ранее высказывал и Альберти: "Здание есть как бы живое существо, создавая которое следует подражать природе ".

Гармонию в природе естествоиспытатели видят в целесообразном и совершенном устройстве мироздания, которое находит выражение в "красивых" математических уравнениях и принципах симметрии (см. гл. 4). Гармонию в архитектуре зодчие рассматривают как сложную иерархическую систему, которая связывает все элементы архитектурной композиции в единое художественное целое и которая проявляется опять-таки в математических законах, законах пропорциональности. Так, Жолтовский считал, что гармония в природе и гармония в архитектуре обретают одинаковое математическое выражение в законе золотого сечения.

Пропорциональность является наиболее ярким, зримым, объективным и математически закономерным выражением архитектурной гармонии. Пропорция - это математическая закономерность, прошедшая через душу зодчего, это поэзия числа и геометрии в его архитектурном языке. Вот почему на языке пропорций говорили зодчие всех времен и всех архитектурных направлений: древние египтяне и древние греки, средневековые каменотесы и древнерусские плотники, представители барокко и классицизма, коструктивисты и рационалисты, апологеты эклектизма и функционализма, поклонники "модерна" и "хайтека". Правда, некоторые современные зодчие пытаются напрочь исключить пропорции из своего архитектурного арсенала, сделав своим кумиром "геометрию беспорядка". Вот как им отвечает французский теоретик искусства М. Гика: "И гордый геометр, создавший план Великой Пирамиды, и зодчие, и философы века Перикла, ... и Альберти, и Леонардо да Винчи, и Джакопо да Барбари (его ученик) думали, что как в живой природе, так и в искусстве, являющемся ее эманацией, беспрестанно проявляется закон Числа. Браманте, Рафаэль, Микеланджело и Виньола думали так же и считали, что совершенное знание геометрии и непрестанное размышление о законах "науки пространства" необходимы каждому, кто призван создавать или закреплять формы при помощи кисти, резца или шнура. Может быть, они преувеличивали? Но может быть, преувеличиваем мы, недооценивая геометрию?"

К сожалению, ни древние египтяне, ни древние греки, ни средневековые каменщики, ни плотники Древней Руси не сохранили для потомков секреты своих пропорций. Ни в уцелевших фрагментах пифагорейцев, ни в трудах Платона, Аристотеля, Архита, Евклида, Архимеда, Аполлония нет ни намека на теорию архитектурных пропорций. И это в то время, когда Пифагор знал, по крайней мере, три вида "древних" пропорций (5.1), когда Платон в "Тимее" доказывал, что красота полностью зависит от совершенства пропорций, а Евклид в "Началах" дал развитое математическое учение о пропорциональности и применял правило золотого сечения для построения правильного пятиугольника! Единственное дошедшее до нас античное сочинение о зодчестве - это знаменитые "Десять книг об архитектуре" Витрувия, время написания которых относят к 27 - 14 гг. до н. э.

"Десять книг" Витрувия в архитектуре, как и "Начала" Евклида в математике, - это энциклопедия античных знаний, это не только собственное сочинение автора, но и собрание известных к тому времени трудов в данной области. Сам автор ни в коем случае не скрывал этого, более того: "Что до меня, о Цезарь, то я не выпускаю этого сочинения под своим именем, заметая следы чужой работы, и не намерен доказывать свою правоту, опорочивая чьи-либо мысли, но, напротив, я приношу бесконечную благодарность всем писателям за то, что, собрав из прошлого превосходные творения человеческого гения, они, каждый в своем роде, накопили изобильные запасы знаний, благодаря которым мы, как бы черпая воду из источника и проводя ее для собственных нужд, имеем возможность писать красноречивее и свободнее и, опираясь на таких авторов, осмеливаемся давать новые наставления".

Не правда ли, превосходный урок научной этики преподал Витрувий 2000 лет тому назад!

Вот почему после "Начал" Евклида (ок. 300 гг. до н. э.), "Альмагеста" Птолемея (ок. 150 гг. до н. э.) и "Десяти книг об архитектуре" Витрувия (ок. 20 гг. дон. э.) труды многих предшественников этих ученых в математике, астрономии и зодчестве стали представлять интерес лишь для историков науки. Однако такая "собирательность" (по-латыни - "компилятивность") не умаляет достоинств названных авторов, ибо, как сказал однажды выдающийся немецкий математик Давид Гильберт (1862 -1943), значение научной работы можно измерить числом предыдущих публикаций, которые стали ненужными после появления этой работы.

Но в теории архитектурных пропорций энциклопедии античного зодчества Витрувия суждено было стать источником глубоких заблуждений. Дело в том, что в своем сочинении Витрувий справедливо называет совершенными те сооружения, в которых достигнута "точная соразмерность" всех частей с основной мерой. Однако какой математический смысл вкладывал автор в эту фразу, оставалось неясным. После падения Рима о Витрувий, как и о всей античной "премудрости", надолго забыли, и только через тысячу лет, в 1414 г., в монастыре Сен-Галлен в Италии был случайно обнаружен единственный экземпляр трактата. "Десять книг" мгновенно стали настольной книгой зодчих итальянского Возрождения, страстных поклонников античной классики. Авторитет Витрувия был огромен. Еще бы: ведь ему посчастливилось читать пропавший трактат самого создателя Парфенона, зодчего Иктина "О соразмерности дорийского храма на Акрополе"! И вот с тех пор "точную соразмерность", о которой говорит Витрувий, стали понимать в простейшем арифметическом смысле - как кратность всех частей сооружения основному модулю. Поясним, что это значит.

Модуль в архитектуре (от лат. modulus - мера) - это единица измерения, принимаемая для согласования размеров частей сооружения между собой и со всем сооружением. В качестве модуля в зависимости от особенностей конструкции и композиции здания принимались различные величины, например диаметр колонны в античной архитектуре или диаметр купола в византийском зодчестве. Еще чаще использовали так называемый линейный модуль, когда архитектурной мерой являлась непосредственно мера длины. В истории всех народов меры длины (вплоть до 10 декабря 1799 г., когда впервые была введена искусственная мера длины - метр) всегда естественным образом связывались с человеком: шаг, сажень, стопа, пядь, фут, дюйм, ярд... (Последний, например, был введен в 1101 г. указом английского короля Генриха I и равнялся расстоянию от кончика носа его величества до конца среднего пальца его вытянутой руки.) Так вот, "точную соразмерность" теоретики Возрождения поняли арифметически: модуль должен целое число раз ("точно"!) откладываться в каждой из частей архитектурного сооружения. Таким образом, в теории архитектуры допускались только рациональные пропорции, отношения целых чисел, а об иррациональных пропорциях не могло быть и речи. Это убеждение подкреплялось и тем, что в музыке, как мы знаем, со времен Пифагора также господствовали целочисленные отношения интервалов.

Но сами шедевры древней архитектуры безмолвно взывали к обратному: античные пропорции основаны на иррациональных отношениях! В самом деле, ведь "точную соразмерность" частей и целого можно достигнуть и другим путем - геометрическим. Например, построив квадрат со стороной АВ и измерив шнуром его диагональ АС, нетрудно было получить иррациональную пропорцию АВ/АС = 1/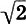, даже не зная иррациональных чисел. Далее, отложив с помощью шнура на продолжении стороны АВ диагональ AC = AD, легко было построить прямоугольник с иррациональным отношением сторон DE/AD = 1/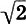. Повторив эту операцию несколько раз, можно получить систему прямоугольников с иррациональными отношениями сторон. Ясно, что прямоугольник AHKN на рисунке (б) состоит из двух квадратов. Таким образом, мы получаем еще один практически удобный способ получения иррациональных отношений - систему двух квадратов. Два квадрата, приставленных один к другому, дают иррациональные отношения ВС/АС = 1/√5, АВ/АС = 2/√5, а с помощью двух операций циркулем или шнурком, как показано на рисунке (в), в них можно получить и золотое сечение ЕВ/АЕ = АЕ/АВ = (√5 - 1)/2 = φ, АВ/АЕ = АЕ/ЕВ=1/φ = (√5 + 1)/2 = Φ (см. (12.1)-(12.3)).

Помимо гипотез, построенных на изучении геометрических свойств античных памятников, были и "материальные" свидетельства того, что древние пользовались иррациональными пропорциями. История сохранила имена древнейших математиков и зодчих - Имхотепа и Хесиры, живших в XXVIII веке до н. э., - строителей первой в истории Древнего Египта пирамиды фараона Джосера в Саккаре. Это были высокочтимые люди, о чем свидетельствуют древнеегипетские иероглифы: "Визирь фараона Нижнего Египта, первый после фараона Верхнего Египта, управитель великой палаты, почетный гражданин, великий жрец Гелиополиса, Имхотеп, строитель и скульптор"; "Хесира, начальник Дестиутса и начальник Бута, начальник врачей, писец фараона, приближенный фараона, жрец Гора, главный архитектор фараона, Верховный начальник десятки Юга и резчик". Хесира был похоронен вблизи пирамиды Джосера. Стены его гробницы украшали рельефы на досках. Поистине потрясающе, что древние доски, которым почти 5000 лет, прекрасно сохранились и выставлены сегодня в Египетском музее в Каире. На двух панелях изображены фигуры владельца гробницы, которые считаются лучшими образцами рельефного портрета в древнеегипетском искусстве. Но для нас эти рельефы интересны прежде всего потому, что в руках у Хесиры, помимо прибора для письма, изображены две палки - два эталона меры. Если теперь взять линейку, измерить Длины этих палок и найти их отношение, то мы обнаружим, что они относятся как 1/√5 = 0,447!

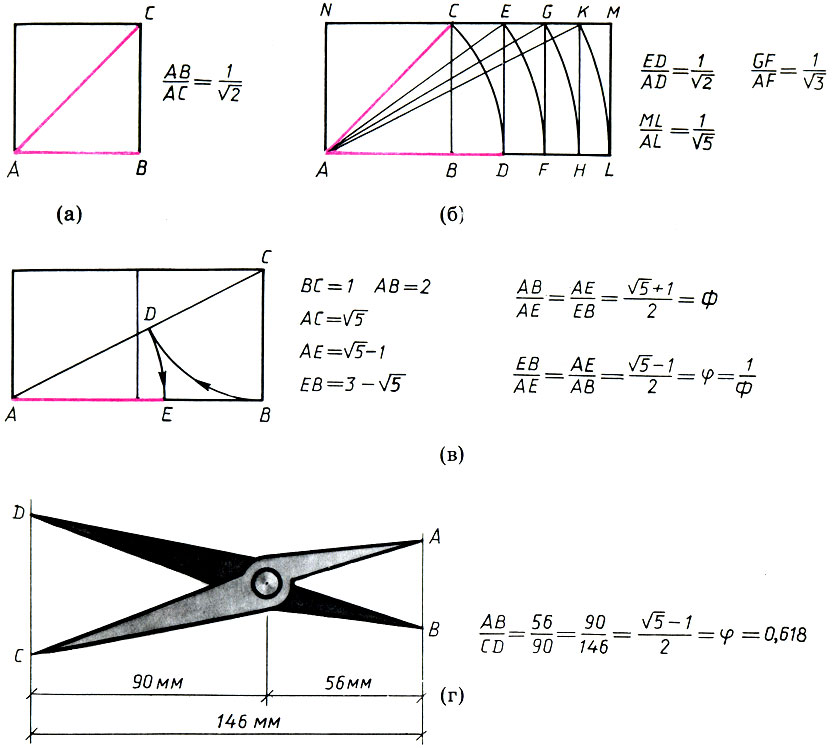
Примеры геометрического построения иррациональных отношений. Диагональ квадрата (а). Система прямоугольников с иррациональными отношениями сторон (б). Золотое сечение в системе 'двойной квадрат' (в). Помпейскйй пропорциональный циркуль, установленный на золотое сечение (г)

Зодчий Хесира. Фрагмент деревянной панели из гробницы Хесиры в Саккаре. XXVIII в. до н. э. Рельеф Хесиры - не только лучший образец древнеегипетского рельефного портрета, не только древнейшее в мире художественное произведение на дереве, но и научное свидетельство о древнеегипетской системе архитектурного пропорционирования

Существует и еще одно удивительное свидетельство мудрости древних. В Неаполе, в Национальном музее, хранится пропорциональный циркуль, найденный при раскопках в Помпеях. Пропорциональный циркуль является необходимым атрибутом архитектора. Он состоит из двух равных подлине ножек, скрепленных винтом наподобие ножниц, и позволяет (минуя вычисления!) для любого отрезка получать отрезок, находящийся с ним в заданном отношении. Действие пропорционального циркуля основано на подобии треугольников и не требует особых комментариев (г). Так вот, помпейский циркуль наглухо закреплен в отношении золотого сечения! Это легко проверить, зная размеры циркуля, которые на рисунке (г) указаны в миллиметрах.

Кроме помпейского, особый интерес представляет циркуль из Музея терм в Риме. Он также имеет длину вполовину римского фута - 146 мм, но настроен на другую иррациональную пропорцию (больший отрезок - 92 мм, меньший - 52 мм):

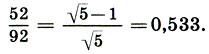
Геометрически эта пропорция означает отношение отрезка AD ко всей диагонали АС (см. с. 199). Как считает архитектор П. Ш. Шевелев, именно с помощью такого циркуля мог быть построен чертеж Парфенона.

Но, несмотря на многие доказательства, авторитет Витрувия (возможно, и неправильно понятого), авторитет модульной системы в архитектуре, был столь велик, что мысль о геометрическом построении иррациональных пропорций древними оформилась лишь к XX веку. Но как именно, по какой системе древние строили свои замечательные пропорции? Это по-прежнему оставалось тайной, и здесь теоретики архитектуры могли довольствоваться лишь гипотезами. Стремление познать тайны древних пропорций было огромным. Еще бы: ведь это дало бы ключ к созданию новых шедевров!

Естественно, что каждый автор стремился проверить свою теорию на пропорциях Парфенона. Парфенон был и остается совершеннейшим из архитектурных сооружений, архитектурной скульптурой, мраморным сводом законов античного зодчества. Уникальность и бессмертие Парфенона осознавали уже в античности. Вот как писал о Парфеноне в I веке древнегреческий писатель, историк и философ Плутарх (ок. 46 - ок. 127): "Так вырастали эти строения, гордые в своем величии, непревзойденные по своей волшебной красоте. Такими они были потому, что мастера старались превзойти друг друга, каждый из них свое ремесло превращал в художественное творчество... И так эти здания словно дышат молодостью, из века в век защищающей их от зуба времени. Можно сказать, что от этих творений веет ароматом каменных цветов и в них живет душа, которая никогда не стареет".

Теорий античных пропорций, и в частности пропорций Парфенона, становилось все больше. Наконец, к середине XX века их стало столько, что сами архитекторы перестали понимать, какие же из этих теорий справедливы и есть ли среди них таковые. Некоторые архитекторы вообще потеряли веру в пропорции. Вот, например, выдержка из книги архитектора Г. Б. Борисовского " Наука, техника, искусство":

"Все исследователи, почти как правило, дают анализ пропорций Парфенона,

стараясь привлечь его в качестве авторитетного свидетеля правоты их теории. Это делают Тирш, Цейзинг, Жолтовский, Гримм и др. Все ищут в нем именно тот порядок, который они отстаивают своей теорией. Если сопоставить эти анализы, то обнаружится несколько странная ситуация.

Тирш еще в прошлом столетии заявил: пропорции Парфенона построены на подобии. Вот чертеж, неоспоримо доказывающий это. (Чудесно,- говорят все.)

Цейзинг уверяет: в основе пропорций Парфенона лежит золотое сечение. Вот чертеж, это подтверждающий. (Все в восхищении.)

Жолтовский считает: Парфенон зиждется на золотом сечении. И дает совершенно иной чертеж, неоспоримо подтверждающий это. (Все в восторге.)

Гримм утверждает то же, что Цейзинг и Жолтовский, и приводит другой чертеж, не менее убедительный, хотя и совсем не похожий на два предыдущих. (Все в изумлении.)

Хэмбридж утверждает: пропорции Парфенона складываются из динамических прямоугольников. Вот чертеж, неоспоримо это доказывающий. (Все аплодируют.)

Мессель заявляет: пропорции Парфенона основаны на членении окружности. Вот чертеж, убеждающий нас в этом. (Аплодисменты, переходящие в овацию.)

Не так давно архитектор И. Шевелев опубликовал статью и небольшую книгу, в которой утверждает, что пропорции Парфенона основаны на соотношении 1:√5, и представляет чертеж с расчетом, убедительно это подтверждающим. (Аплодисментов пока не слышно.)

Явно здесь что-то не так ..."

Действительно, глядя на различные чертежи пропорций Парфенона, кажется, что между ними нет ничего общего. Между тем здесь все "так". Различные анализы пропорций Парфенона - это различные доказательства "теоремы Парфенона", которая, как и теорема Пифагора, имеет много доказательств. Но от этого "теорема Парфенона" не становится хуже (или вовсе перестает существовать, как кажется Борисовскому), а, напротив, предстает перед нами во всем своем богатстве и красоте. Ибо множество доказательств свидетельствует о большом числе конкретных реализаций, о "всеобщности" доказываемого, а всеобщность является одним из признаков красоты науки (см. с. 29, 30).

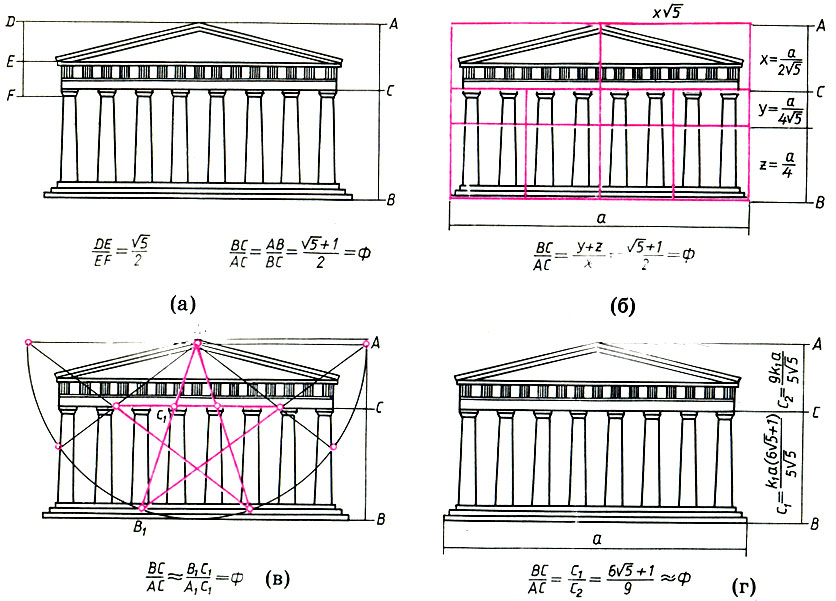
Различные методы анализа пропорций Парфенона: Жолтовский (а), Хэмбидж (б), Мессель (в), Шевелев (г)

В самом деле, Тирш говорит о подобии. Но подобие - это геометрическое выражение пропорциональности.

Цейзинг и Жолтовский уточняют: в пропорциях Парфенона имеется золотое сечение. В частности, в золотой пропорции соотносятся главные вертикальные размеры портика: высота ВС поддерживающих частей (основание и колонны) и высота АС поддерживаемых частей (антаблемент и фронтон).

Гримм, воспитанный на целочисленных музыкальных пропорциях Возрождения, считает, что главные вертикали Парфенона находятся в отношении малой сексты (8/5). Казалось бы, совершенно иной, "музыкальный", подход. Но и здесь нет противоречия с Цейзингом и Жолтовским, ибо 8/5, как будет показано в следующей главе, есть отношение двух членов ряда Фибоначчи и является одним из рациональных приближений коэффициента золотого сечения Ф (8/5 = 1,600; Φ ≈ 1,618). Гримм правильно заметил, что золотое сечение в главных вертикалях Парфенона выдержано лишь приблизительно, и этим уточнил Цейзинга и Жолтовского.

Но все эти исследования носили эмпирический характер и не давали целостной системы античного пропорционирования. Первой такой попыткой была система динамических прямоугольников американского искусствоведа Хэмбиджа. Прямоугольники с иррациональным отношением сторон Хэмбидж называет динамическими, связывая с ними идею роста, движения и гармонии в природе и искусстве. Особую роль Хэмбидж отводит прямоугольнику с отношением сторон 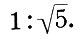. Хэмбидж разбивает фасад Парфенона на ряд динамических прямоугольников (l:√5) и квадратов (1:1). Здесь все ново и спорно: и подход, и метод, и чертеж. Но что будет с интересующими нас главными вертикалями? Выражая вертикальные элементы х, у, z через ширину основания а:х - а/2√5, у = а/4√5, z = а/4, легко видеть, что главные вертикали Парфенона по-прежнему находятся в золотой пропорции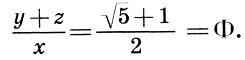

Метод пропорционирования немецкого теоретика Месселя основан на десятикрат ном делении окружности. Мессель считает, что обычный циркуль (или шнур) являлся основным рабочим инструментом античного и средневекового зодчего. Подход Месселя также оригинален и также спорен во всех аспектах, кроме одного - математического. Действительно, как мы увидим в следующей главе, при делении окружности на десять частей можно получить весь ряд золотого сечения (12.4)! Поэтому В₁С₁:С₁А₁ = Φ ≈ВС:СА, т. е. интересующие нас главные вертикали Парфенона приблизительно находятся в золотой пропорции.

В главе 16 мы подробнее познакомимся с системой пропорционирования Шевелева и покажем, что в этой системе для главных вертикалей также приближенно выполняется золотая пропорция.

Заметим, что во всех случаях приближенного выполнения пропорции золотого сечения ошибка не превышает 1%. К сожалению, существующие обмеры Парфенона выполнены примерно с такой же точностью и поэтому не могут служить критерием истинности теории. Но и более тщательные обмеры Парфенона нужно будет осторожно применять в качестве критерия истины, ибо при строительстве сооружения 2500 лет назад, разумеется, могли быть допущены отклонения от замысла автора.

Вот почему главным критерием истинности той или иной гипотезы будет оставаться ее логическая непротиворечивость, ее математическая целостность. Этим требованиям, по нашему мнению, наиболее полно удовлетворяет система Шевелева, которая не получила еще должного признания. Система Шевелева позволяет из одного размера - ширины стилобата (верхней ступени основания) - получить все размеры Парфенона в диапазоне от 69,5 м (длина стилобата) до 16 см (высота шейки капители)! Таким образом, именно в системе Шевелева выполняется принцип гармонии Гераклита: "из всего - единое, из единого - все".

Итак, главный вопрос о том, какой системой пропорций пользовался гениальный создатель Парфенона зодчий Иктин, пока остается открытым. Заметим, что мы остановились только на соотношении двух главных вертикалей Парфенона. В золотой пропорции соотносятся и многие другие элементы Парфенона, однако подробный анализ пропорций этого великого архитектурного памятника занял бы объем, по крайней мере равный объему всей этой книги. Мы же в нашем кратком обозрении убедились, что разговор об архитектурных пропорциях неизбежно приводит к золотой, или, как ее называли во времена Возрождения, божественной пропорции. Поэтому нам необходимо подробнее познакомиться с математическими свойствами этого интереснейшего феномена.