
12. Математический анализ музыки
Чрезвычайная бедность, шаткость и разрозненность существующих основ музыкальной эстетики побуждает нас пытливо всматриваться во всякое закономерное явление, относящееся к этой области, в надежде приподнять хотя бы уголок изидовой завесы, скрывающей от нашего умственного взора таинственные творческие законы природы...
До сих пор в нашем разговоре о музыке мы фактически не выходили за пределы одной октавы. С одной стороны, это хорошо, ибо говорит о том, сколь много мудрости в простоте знакомых каждому семи нот октавы. Но с другой стороны, безусловно, непростительно по отношению к музыке в целом, ибо музыка - это прежде" всего мелодия, это песня души. Ведь, как сказал Пушкин,
Из наслаждений жизни Одной любви музыка уступает, Но и любовь - мелодия...
Говоря о музыке, хочется вспомнить и слова философа и поэта Вильгельма Генриха Ваккенродера (1773-1798), который, прожив неполные 25 лет, вошел в историю как родоначальник немецкого романтизма: "Но музыку я считаю самым чудесным из всех этих изобретений, потому что она описывает человеческие чувства сверхчеловеческим языком, ибо она показывает все движения нашей души в невещественном виде, вознося их над нашими головами в золотых облаках эфирных гармоний..."
Прошло 25 веков с тех пор, как великий Пифагор и его ученики открыли законы целочисленных отношений в музыке и дали математическое построение музыкальной гаммы. Однако до сих пор в математическом анализе мелодии, музыкального произведения в целом делались только робкие шаги. Лишь к середине XX века, который часто называют веком науки, произведения искусства стали подвергаться изучению математическими методами. Причиной тому является проникновение науки во все сферы общественной жизни, а значит, и математизация человеческого знания, о которой говорилось в главе 2. Опыты по применению "точных методов" к изучению искусства являются частью этого общенаучного процесса.
Разумеется, математические методы в искусствознании применяются не для того, чтобы алгеброй вытеснить гармонию, а чтобы подтвердить интуицию художника, полнее раскрыть замысел гения, а быть может, и найти закономерности, отличающие совершенное произведение или хотя бы эпоху, в которую оно создано. Как говорил Пуанкаре, "Математика - это искусство называть разные вещи одним и тем же именем". Поэтому проникновение математических методов в анализ произведений искусства, безусловно, поможет назвать одним именем пока непонятные и несвязанные между собой законы искусства.
К сожалению для исследователя и к счастью для художника, законы искусства не столь прямолинейны и однозначны, как законы науки или языка. Эта "нелинейность" законов искусства и создает неимоверные трудности на пути исследователя искусства, но в то же время является источником все новых открытий в творчестве художника. Более того, искусство парадоксально и его парадоксальность не в состоянии выразить строгое логическое мышление. Вот только два примера из живописи. Какими законами механики описать движение саней, в которых едет суриковская боярыня Морозова? Уже сто лет, как бегут ее сани, бегут, оставаясь все время на одном месте... "Джоконда" Леонардо да Винчи и "Неизвестная" Крамского явно глядят на кого-то. Смотрят пристально, грустно и чуть усмехаясь, надменно и страдальчески, но смотрят на того, кого нет. Кипы статей написаны о том, на кого и как они смотрят, но все безрезультатно. Математика также бессильна перед чарами этих двух загадочных женщин.
Но у математики непочатый край проблем и в тех областях искусства, которые поддаются законам логики. Ведь математика делает только первые шаги в анализе искусства, которые сродни первым шагам медицины, начавшей изучение живого организма человека с познания законов его анатомического строения. Хорошо сказал об этом русский советский музыковед Э. К. Розенов (1861 - 1935): "Хотя, обнаруживая в живом творчестве и в созданном им живом художественном организме его сокрытый от взора внутренний механизм, притом, конечно, не весь, а одну какую-нибудь из двигающих его пружин, мы не дальше продвинемся по пути к проникновению в жизненные тайны, чем это делает анатомия, обнажающая скелет, мускулы и нервы живого организма, тем не менее мы не должны считать такие исследования бесцельными".
В начале нашего столетия на одном из заседаний Московского научно-музыкального кружка, членами которого вместе с композиторами и пианистами Танеевым, Рахманиновым, Глиэром, Гольденвейзером были и крупные московские ученые, Розенов выступил с докладом "Закон золотого сечения в поэзии и музыке". Эту работу можно считать одним из первых математических исследований музыкальных произведений. Остановимся на ней подробнее.
Очевидно, что при делении целого на две неравные части возможно бесконечное множество отношений между целым и одной из его частей, а также между самими частями целого. Но только в единственном случае эти отношения могут быть равными. Этот случай, как мы знаем (с. 79), и представляет собой золотое сечение, когда целое относится к большей части, как большая часть к меньшей.
Обозначая целое через а, большую часть х и, следовательно, меньшую а - х, имеем
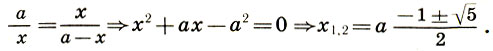 (12.1)
(12.1)Поскольку х есть часть целого, т. е. величина положительная, а второй корень (12.1) отрицателен, то приходим к единственному значению корня:
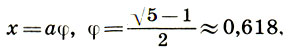 (12.2)
(12.2)где величина φ является коэффициентом золотого сечения. Тогда
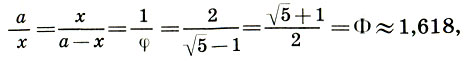 (12.3)
(12.3)причем Ф = 1/φ
Для меньшей части имеем а - х = а(1 - φ) = аφ2, причем аφ + φ2 = а. Разделив теперь величину аφ в золотой пропорции, получим
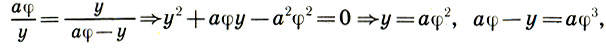
причем аφ2 + аφ3 = аφ. Легко видеть, что большая часть второй золотой пропорции у = аφ2 совпадает с меньшей частью первой а - х = аφ2. Итак, при последовательном делении целого а в золотой пропорции имеет место геометрическая прогрессия (ряд золотого сечения) со знаменателем φ, каждый член которой равен сумме двух последующих членов прогрессии:
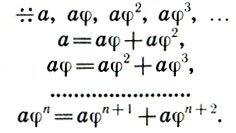 (12.4)
(12.4)Огромная роль золотого сечения в пространственных искусствах (скульптуре, архитектуре, живописи) известна с античных времен и имеет немало объяснений. Например, такое: линия глаз, на которой человек привык концентрировать свое внимание, слушая собеседника, делит длину лица в отношении золотого сечения. Поэтому при взгляде на любой предмет мы невольно направляем глаза в точку золотого деления, которая кажется нам привычной, естественной, а потому и красивой. Что касается искусств, развивающихся во времени (поэзия, музыка), то здесь неизвестны аналогичные природные предпосылки закона золотого сечения. Но тем более удивительным оказывается действие этого закона в поэзии и музыке, которое, по-видимому, первым обнаружил Розенов.
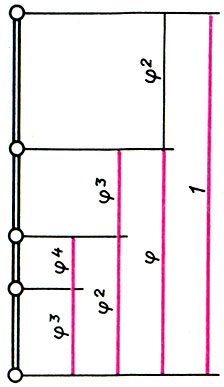
Последовательное деление единичного отрезка в золотом сечении
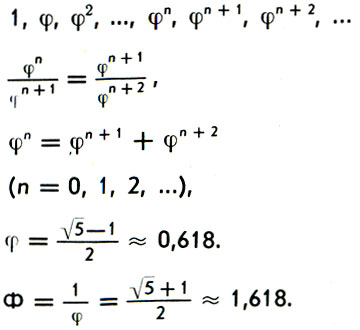
Ряд золотого сечения
Розенов проанализировал "популярнейшие и наиболее излюбленные произведения гениальных авторов Баха, Моцарта, Бетховена, Шопена, Вагнера, Глинки, а также произведения народного творчества наиболее древнего происхождения, живучесть которых является достаточным доказательством их эстетической ценности и широкой популярности". Остановимся на анализе Хроматической фантазии и фуги И. С. Баха, которые объединены общей тональностью ре минор и контрастны по жанру и образу. Хроматическая фантазия с фугой ре минор - одно из величайших творений Баха, образец совершенства формы и содержания, "могущественнейшее клавесинное произведение" (А. Н. Серов).
Хроматическая фантазия написана в размере 4/4, имеет 79 тактов, т. е. 79*4 = 316 четвертных долей. Итак, "целое" а = 316. Фантазия состоит из двух ясно различимых по характеру частей, отделенных друг от друга паузой. Первая часть, прелюдия, заканчивается на арпеджированном доминантовом трезвучии с разрешением на 2-й четверти 49-го такта, на которой стоит знак ферматы (удлинение звука), и затем идет пауза. Таким образом, первая часть фактически заканчивается на 3-й четверти 49-го такта, т. е. на 195-й (48*4 + 3) четверти (а1 =195). Вторая часть, пишет Розенов, "состоит из ряда в высшей степени выразительных колорированных речитативов, то развивающихся по силе, энергии и размаху До гигантской мощи, то нежных и жалобных, то сердитых и запальчивых, то впадающих в необычную для той эпохи романтическую мечтательность". На вторую часть приходится 121 четверть (а2 = а-а1 = 316 - 195 = 121). Вычисляя "теоретическую" длину первой части с помощью коэффициента золотого сечения, мы с поражающей точностью находим а1= аφ = 0,316-0,618 = 195,3! Итак, Хроматическая фантазия разделена на первую и вторую части в золотой пропорции :
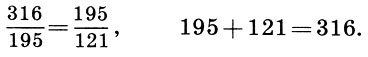
Но на этом чудеса гениального творения Баха только начинаются. Построив ряд золотого сечения (12.4) при а = 316, имеем
316 195,3 120,7 74,6 46,1 28,5 17,6.
Каково же должно быть наше удивление, когда мы обнаружим, что на 124-й четверти находится кульминация первой части и стоит знак ферматы, а на 77-й четверти от начала второй части имеет место кульминация второй части! Таким образом, кульминация обеих частей с небольшой погрешностью, легко объяснимой растяжимостью темпов, делит эти части по закону золотого сечения. Далее, каждый из полученных четырех разделов Хроматической фантазии имеет характерные особенности, которые также с потрясающей точностью приходятся на точки золотого деления этих разделов! Наконец, Розенов нашел и более мелкие деления Хроматической фантазии в золотой пропорции, на которых мы не будем останавливаться.
Итак, Хроматическая фантазия, произведение свободного по форме жанра, буквально соткано из золотых пропорций! Пожалуй, эстетическое впечатление от математического анализа Хроматической фантазии имеет не меньшую силу, чем прослушивание бессмертного творения Баха. А взятые вместе - чувственное впечатление и рациональный анализ, безусловно, позволяют еще на один шаг приблизиться к сокровенным тайникам гения.
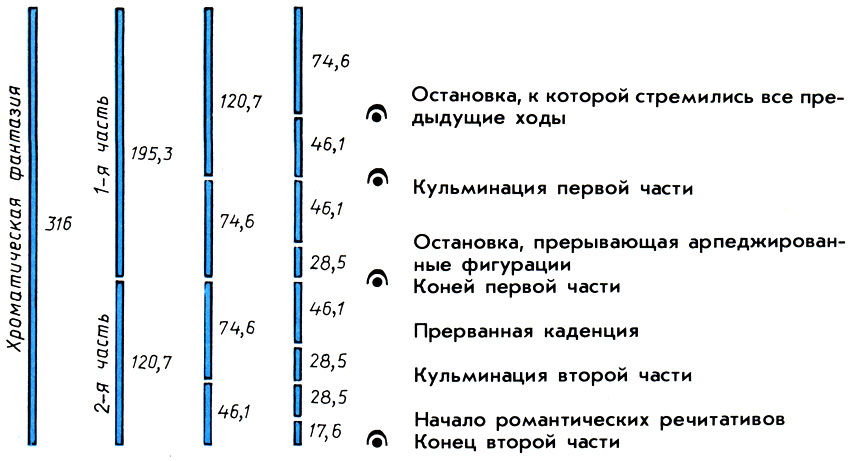
Главные золотые сечения Хроматической фантазии И. С. Баха. Цифры обозначают число четвертей теоретического ряда золотого сечения (а = 316). Справа дано описание соответствующих характерных мест нотного текста фантазии
Перейдем к анализу фуги. Фуга (от лат. fuga - бег) является наиболее совершенной формой многоголосной музыки (полифонии). Фуга строится на многократных проведениях (повторениях) основной музыкальной темы в разных голосах. Проведения основной темы обычно перемежаются в фуге с промежуточными вставками, называемыми интермедиями. Таким образом, фуга в отличие от фантазии имеет четко определенный закон построения. Но тем не менее точность "математического" построения фуги ре минор просто поражает!
Фуга ре минор состоит из семи пар проведений и интермедий и двух самостоятельных проведений. Из семи пар "проведение-интермедия" пять пар строго подчиняются закону золотого сечения. Те же две пары "проведение-интермедия", для которых закон золотого деления не выполнен, являются своеобразными центрами симметрии относительно обрамляющих их разделов фуги и с каждым из них находятся в золотой пропорции! Именно для того, чтобы выделить эти два центра симметрии, Бах специально допускает в их строении отклонения от золотого деления и делает эти две пары "проведение-интермедия" симметричными.
На рисунке приведена схема строения фуги ре минор. Здесь же указано число четвертей в каждом разделе фуги (целые числа) и даны теоретические значения членов золотой пропорции (дробные числа). Как видим, все пять пар "проведение-интермедия" с изумительной точностью разделены в золотой пропорции (абсолютные ошибки колеблются в диапазоне от 0,05 до 0,15 четверти, относительные ошибки - от 0,02% до 0,7%). Таким относительным погрешностям могут позавидовать многие из современных инженерных расчетов! В более крупных разделах абсолютные ошибки, естественно, возрастают. Но и при делении самого большого раздела (91 четверть) эти ошибки не превышают 1,25 четверти. Не следует, однако, забывать, что мы имеем дело с художественным произведением. Отметим, что в фуге ре минор существуют также и более мелкие, и более крупные соотношения золотого сечения, на которых мы просто не останавливаемся.
Итак, простой математический анализ, не выходящий за рамки арифметики, позволяет совершенно иными глазами взглянуть на музыкальное произведение, увидеть его скрытую внутреннюю красоту, которую мы только ощущаем, слушая произведение, и которую мы "видим", проводя его математический анализ. Вот как сказал об этом Розенов: "При взгляде на схемы Хроматической фантазии и фуги... невольно приходишь в священный трепет перед гениальностью мастера, воплотившего силой художественной чуткости до такой степени точности законы природного творчества".
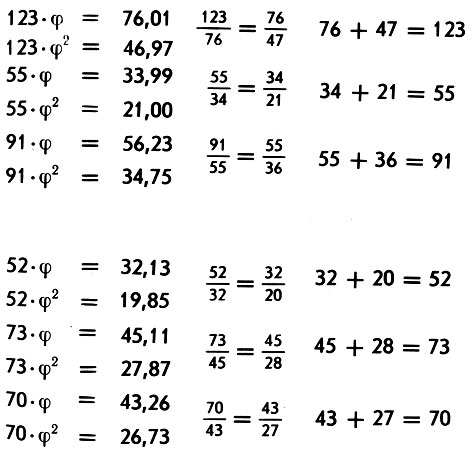
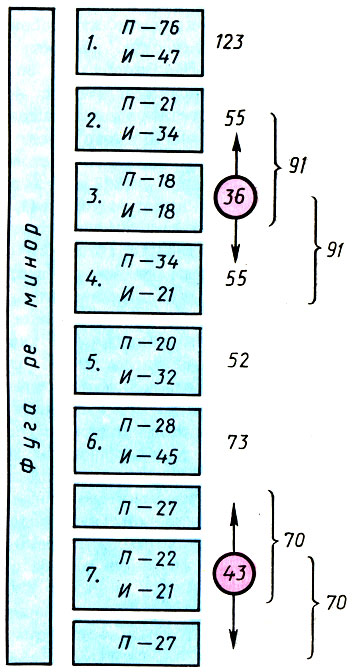
Строение фуги ре минор И. С. Баха. Целые числа указывают число четвертей в фуге, дробные - теоретические значения золотых сечений. Золотые пропорции в более крупных частях фуги отмечены фигурными скобками, центры симметрии - кружками. П - проведение, И - интермедия
Далее Розенов, "дабы показать, что приведенный пример не является у Баха исключительным", рассматривает многочисленные прелюдии и фуги из "Хорошо темперированного клавира" Баха, а также оперу Моцарта "Дон-Жуан", финал знаменитой "Лунной" сонаты Бетховена, Фантазию фа минор Шопена, вступление к опере "Тристан и Изольда" Вагнера, увертюру к опере "Руслан и Людмила" Глинки и многие народные песни. Во всех этих произведениях Розенов с замечательной точностью обнаруживает действие закона золотого сечения. "Приведенные мною примеры проявления закона золотого сечения настолько характерны и замечательны,- пишет Розенов,- что исключают всякую возможность отрицания эстетического значения этого закона в музыке". Не правда ли, здесь мы имеем тот самый случай, когда "цифры могут представлять собой культурную и эстетическую ценность"? (См. высказывание Н. Винера в эпиграфе к первой части книги.)
Но помимо установления самого факта наличия закона золотого сечения в музыкальных произведениях и его огромного эстетического значения в музыке математический анализ музыки (даже такой элементарный) позволяет сделать некоторые выводы о характерных особенностях творчества самих композиторов. Так, сравнивая проявление закона золотого сечения у Баха и Бетховена, Розенов пишет: "Мы находим у Баха сравнительно более детальную и органическую сплоченность. Закон золотого деления проявляется у него с поразительной точностью в соотношениях крупных и мелких частей как в строгих, так и в свободных формах, что, несомненно, соответствует с характером этого гениального мастера-труженика, сильным, здоровым и уравновешенным, с его глубоко сосредоточенным отношением к работе и детально отделанной манерою письма. У Бетховена проявление закона золотого сечения глубоко логично по отношению к размерам частей формы, но главным образом указывает на силу темперамента этого автора по точности совпадения всех моментов высшего напряжения чувств и разрешения подготовленного ожидания с моментами золотых сечений. У Шопена внутренняя формальная связь сравнительно слабее и проявляется не сплошь, а лишь местами. По силе темперамента он сходен с Бетховеном, но проявление это более внешне и касается чаще изящной нарядности изложения мысли, нежели его внутренней логики. У Моцарта темперамент проявляется сравнительно слабее, закон золотого сечения направлен у него особенно часто к подчеркиванию драматических элементов (психологических контрастов, противопоставлений характеров) и трагических положений. У Глинки мы находим применение данного закона только лишь в широких масштабах при полном почти отсутствии мелочных соответствий, встречающихся так часто у Баха и Шопена".
Вот к каким глубоким эстетическим выводам приводит простейший математический анализ музыки! Слова Розенова о том, что закон золотого сечения "может, по-видимому, явиться в дальнейшем немаловажным вкладом в экспериментальную эстетику", оказались пророческими. А сама экспериментальная эстетика сегодня обрела наконец права гражданства и уверенно набирает силу.
Из начала XX столетия перенесемся теперь в его вторую половину и перейдем к современным исследованиям по экспериментальной эстетике. Начиная с 1952 г. интересные работы по применению математических методов в исследованиях искусства - литературы, живописи, музыки - публикует видный немецкий ученый Вильгельм Фукс. Фукс - прежде всего физик, работающий в области физики плазмы. Однако у этого ученого-энциклопедиста есть и хобби - исследования в области экспериментальной эстетики, часть из которых собрана в интереснейшей монографии Фукса "По всем правилам искусства". В своих работах по экспериментальной эстетике Фукс стремился показать, что точные методы могут быть эффективно применены к исследованию культурного наследия человечества. Хотя со времен Галилея и Ньютона математическое описание стало великим путем познания природы, применение математического метода к искусству до сих пор вызывало недоверие, сарказм или просто неприязнь. Повинна в этом, скорее всего, все та же инерция мышления, "благодаря" которой в свое время отвергались анатомия и демографическая статистика, считавшиеся уделом лишь Бога и короля. Однако, как отмечает Фукс, "выдающиеся успехи точных наук в присущих им сферах привели к тому, что теперь все более соблазнительной представляется идея испытать методы этих наук и в других областях". В силу известного нам свойства математики "называть разные вещи одним и тем же именем" такие исследования помогли бы выявить общие закономерности в разнородных, на первый взгляд, явлениях культуры. Тем не менее сама постановка подобной проблемы была столь нова и необычна, что Фукс вполне справедливо задавал сам себе вопросы: "Можно ли применять абстрактный аппарат точных наук к явлениям культуры? И если да, то имеет ли это смысл? Будут ли получены при этом результаты, столь же объективные, как и в естественных науках? Удастся ли помимо голых чисел, результатов измерений и статистической обработки фактического материала выявить некий род объективных закономерностей, регулярностей, характерных форм явлений?"
Нам представляется, что работы Фукса дали, бесспорно, положительный ответ на эти вопросы, и мы надеемся, что рассматриваемые далее примеры, относящиеся к математическому анализу музыки, будут тому блестящим доказательством.
Вновь обратимся к анализу высоты музыкальных звуков, которому посвящена практически вся вторая часть книги. На примере многочисленных скрипичных произведений Фукс исследовал, как разные авторы в разные эпохи использовали звуковой материал скрипки. Диапазон звучания скрипки простирается от ноты соль малой октавы до ноты до пятой октавы. Считая энгармонически равные звуки (до-диез = ре-бемоль и т. п.) за один звук, в диапазоне соль-до5мы имеем 54 звука. Пронумеруем их, т. е. каждому звуку скрипки поставим в соответствие число i = 1, 2, ..., 54: соль ⇔ i = l, соль-диез = ля-бемоль ⇔ i = , ля ⇔ i = 3 ..., до5 ⇔ i = 54. Подсчитав общее число звуков N в данном произведении, легко найти относительную частоту появления i-ro звука по формуле
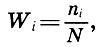
где ni - частота i-то звука, т. е. число появлений i-го звука в произведении. Например, в струнном квартете ми-бемоль мажор Бетховена, в партии первой скрипки N = 3796, а нота соль первой октавы (i = l) встречается 23 раза (n1 =23). Следовательно, ее относительная частота W1= 23/3796 = 0,006. Ясно, что если самые верхние звуки из диапазона звучания скрипки в произведении не используются, то их частота будет равна нулю. Совокупность (i, Wi) i = l, 2, ..., k называется статистическим распределением, а ломаная линия, отрезки которой соединяют точки статистического распределения, называется полигоном относительных частот. Заметим, что поскольку n1 + n2 + ... + nk = N, то W1 + W2 + ... + Wk = (n1 + n2 +... + nk)/N=l, т. е. сумма всех относительных частот статистического распределения равна 1.
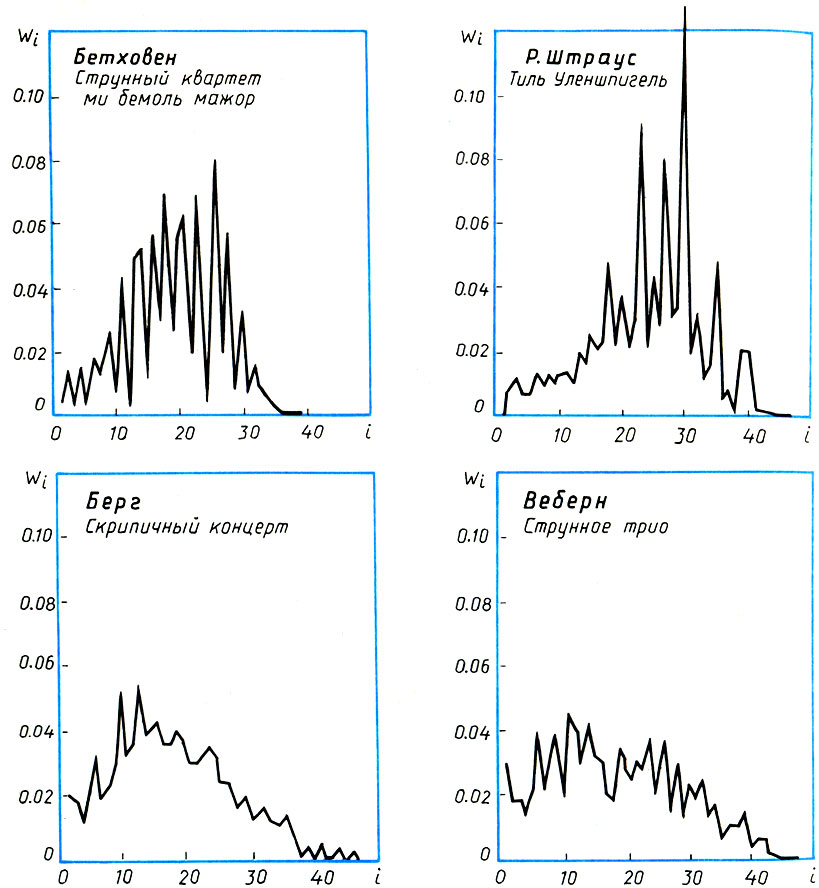
Полигоны относительных частот высоты звуков в партии первой скрипки. Уже по внешнему виду статистических распределений можно заключить, что композиторы-додекафонисты Берг и Веберн применяли совершенно иные правила композиции, чем Бетховен и Рихард Штраус
На рисунке построены полигоны относительных частот высоты звуков в партии первой скрипки для четырех музыкальных произведений: струнного квартета ми-бемоль мажор Бетховена (1809) (партия первой скрипки); симфонической поэмы Рихарда Штрауса "Тиль Уленшпигель" (1890) (партия первой скрипки); первой части скрипичного концерта Берга (1935) и струнного трио Веберна (1927) (партия скрипки). Одного взгляда на рисунок достаточно для того, чтобы понять: первые два произведения - Бетховена и Р. Штрауса, при всем их различии, принадлежат к одному типу музыки, а два последних - Берга и Веберна - к совершенно другому типу (хотя они также отличаются, между собой). Знатоки музыки воспримут этот факт как должное: ведь по отношению к Бетховену и Р. Штраусу Берг и Веберн - представители принципиально иного направления в музыке, так называемой додекафонной* или атональной музыки. Поскольку атональная музыка отрицает главную роль тоники и устойчивых звуков в ладу и считает все звуки равноправными, то и статистическое распределение высот звуков в атональной музыке должно быть более гладким по сравнению с тональной музыкой, где одни звуки являются явно предпочтительными (пики на полигоне относительных частот), а другие употребляются редко ("провалы" на полигоне).
* (Додекафония (от греч. dodeka - двенадцать и phone - звук) - метод музыкальной композиции, основанный на отрицании ладовых связей между звуками. В додекафонии все 12 звуков хроматической гаммы считаются абсолютно равными (откуда и происходит название) без различия устойчивых и неустойчивых звуков и без выделения тоники. Поэтому додекафонию называют также атональной музыкой. Метод додекафонии был разработан и внедрен австрийским композитором Арнольдом Шёнбергом (1874-1951). Альбан Берг (1885-1935) и Антон фон Веберн (1883- 1945) - ученики и последователи Шёнберга.)
Итак, тот факт, что Берг и Веберн - представители одного направления в музыке, а Бетховен и Р. Штраус - другого, нашел яркое выражение в статистических распределениях высот звуков у этих композиторов. Заметим, что Берг и Веберн, будучи пылкими последователями Шёнберга, сочиняли свою музыку по сходным и весьма строгим формальным правилам. Поэтому их статистические распределения так похожи, хотяу с другой стороны, и различаются тонкими деталями, которые характеризуют индивидуальные черты каждого композитора. Таким образом, уже простая статистика высот звуков позволяет выявить, с одной стороны, принадлежность автора к тому или иному направлению в музыке, а с другой - увидеть тонкие черты различия, характерные для конкретных произведений и конкретных композиторов. Однако пока мы ограничивались лишь качественными выводами. Посмотрим, нельзя ли извлечь из статистических распределений какие-либо количественные характеристики.
Всякое статистическое распределение (xi, Wi) i = l, 2, ..., k обладает двумя важнейшими числовыми характеристиками: эмпирической средней и эмпирической дисперсией. Эмпирической средней 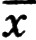 называется среднее арифметическое значений хi, статистического распределения с учетом их частот п" т. е.
называется среднее арифметическое значений хi, статистического распределения с учетом их частот п" т. е.
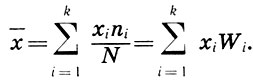 (12.5)
(12.5)
Эмпирическая средняя характеризует "среднюю величину" значений статистического распределения. Однако помимо "средней величины" важно знать, насколько "разбросаны" значения ж, относительно этой средней величины, т. е. какова дисперсия (от лат. dispersus - рассыпанный) статистического рарпределения. Назовем разность xi - 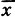 отклонением значения xi от эмпирической средней
отклонением значения xi от эмпирической средней 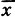 . Легко видеть, что сумма всех отклонений с учетом их частот ni, равна нулю:
. Легко видеть, что сумма всех отклонений с учетом их частот ni, равна нулю:
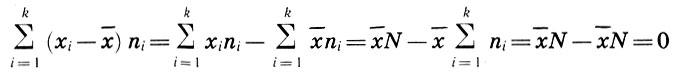
и, значит, не может быть взята в качестве характеристики рассеяния параметров статистического распределения. Поэтому в качестве характеристики разброса параметров xi берут среднее арифметическое квадратов отклонений. Итак, эмпирической дисперсией D называется среднее арифметическое квадратов отклонений значений хi, от их эмпирической средней 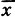 с учетом частот ni, т. е.
с учетом частот ni, т. е.
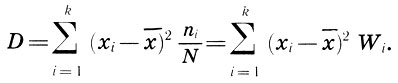 (12.6)
(12.6)Для вычисления эмпирической дисперсии существует также более практичная формула
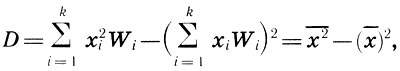 (12.7)
(12.7)т. е. эмпирическая дисперсия равна эмпирическому среднему квадратов значений статистического распределения минус квадрат эмпирической средней. Наконец, чтобы характеристики рассеяния имели ту же размерность, что и значения xi статистического распределения, вместо дисперсии рассматривают среднее квадратическое отклонение
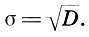 (12.8)
(12.8)
Среднее квадратическое отклонение показывает, насколько узко или насколько широко распределены вокруг эмпирического среднего 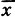 значения статистического распределения xi.
значения статистического распределения xi.
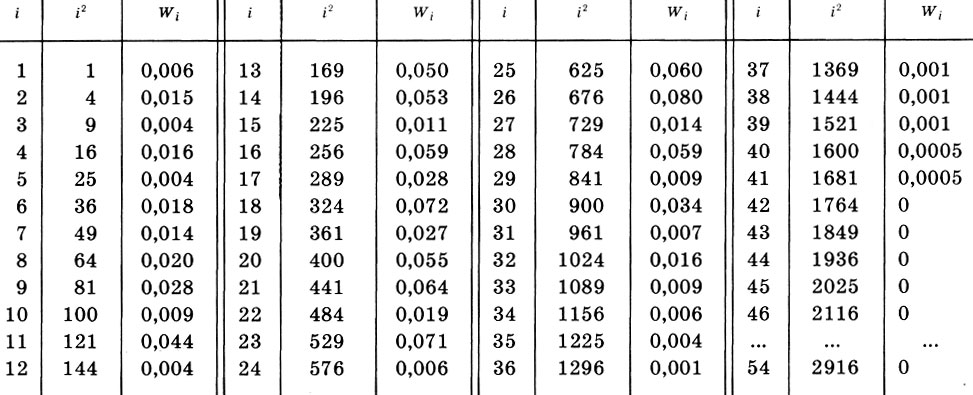
Таблица 3. Статистическое распределение (xi = i, Wi) высоты звуков партии первой скрипки струнного квартета ми-бемоль мажор Бетховена. Для расчета дисперсии приведены также значения xi2 = i2
В качестве примера найдем эмпирическую среднюю, эмпирическую дисперсию и среднее квадратическое отклонение для статистического распределения высоты звуков партии первой скрипки струнного квартета ми-бемоль мажор Бетховена (см. с. 168). Выпишем значения xi = i, xi2 = i2 и Wi (i=l, 2, ..., 54) в виде таблицы 3. Легко проверить, что
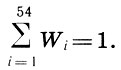
Подставляя данные таблицы 3 в формулы (12.6), (12.7) и (12.8), находим
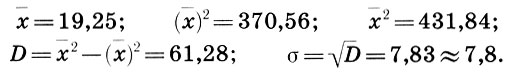
Итак, для струнного квартета Бетховена эмпирическая средняя 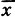 = 19,25, т. е. "средним" звуком произведения является ре-бемоль второй октавы. Это еще мало о чем говорит. Вторая характеристика - среднее квадратическое отклонение - означает, что средний разброс звуков в произведении относительно ре-бемоль составляет ± 8 звуков, т. е. наиболее употребимые звуки произведения находятся в диапазоне 11≤i≤27, или от фа1 до ля2. Среднее квадратическое отклонение высоты звуков музыкального произведения оказалось чрезвычайно эффективной характеристикой, позволяющей найти общие закономерности в развитии всей музыки. Остановимся на этом подробнее.
= 19,25, т. е. "средним" звуком произведения является ре-бемоль второй октавы. Это еще мало о чем говорит. Вторая характеристика - среднее квадратическое отклонение - означает, что средний разброс звуков в произведении относительно ре-бемоль составляет ± 8 звуков, т. е. наиболее употребимые звуки произведения находятся в диапазоне 11≤i≤27, или от фа1 до ля2. Среднее квадратическое отклонение высоты звуков музыкального произведения оказалось чрезвычайно эффективной характеристикой, позволяющей найти общие закономерности в развитии всей музыки. Остановимся на этом подробнее.
Как уже отмечали, основной целью работ Фукса было не просто найти какие-либо числовые характеристики произведений искусства, а выявить на основании этих характеристик закономерности общего порядка. С этой целью Фуксом были составлены статистические распределения высоты звуков в партиях первой скрипки большого числа произведений за период почти в пятьсот лет. Были определены числовые характеристики этих распределений, и прежде всего среднее квадратическое отклонение. Анализ поведения среднего квадратического отклонения дал блестящий результат: среднее квадратическое отклонение за последние 500 лет истории европейской музыки монотонно возрастает. Это уже есть не что иное, как закон развития музыки!
В таблице 4 приведены результаты исследований Фукса. Здесь представлены произведения, написанные с 1530 г. по 1960 г. Для каждого произведения было составлено статистическое распределение высоты звуков в партии первой скрипки, аналогичное таблице 3. Затем были определены средние квадратические отклонения в этих распределениях (найденное нами значение σ = 7,8 для струнного квартета ми-бемоль мажор Бетховена находится в соответствующем месте таблицы 4). Наконец, для каждого периода в истории развития музыки было вычислено среднее арифметическое о средних квадратических отклонений отдельных произведений. Разбиение на периоды проведено в соответствии с существовавшими в музыке направлениями. Так, в таблице 4 полифония строгого стиля представлена произведениями Вилларта, Модены, Палестрины, Хаслера, Шейна и Розенмюллера; полифония свободного стиля (барокко) - произведениями Коре л ли, Вивальди и Баха; классицизм - произведениями Моцарта, Бетховена и Шпора; романтизм - произведениями Шуберта, Шумана, Брамса, Р. Штрауса и Чайковского; неоромантизм - произведениями Хиндемита, Бартока и Эгка; додекафония - произведениями Шёнберга, Веберна, Берга и Ноно. Поэтому естественно, что одни периоды в таблице 4 далеко отстоят друг от друга, а другие - пересекаются. Достаточно одного взгляда на первый и последний столбцы таблицы 4, чтобы увидеть закономерность: за прошедшие 500 лет значение 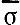 возросло от 3,7 до 10,8, т. е. по мере развития музыки значение σвозрастает.
возросло от 3,7 до 10,8, т. е. по мере развития музыки значение σвозрастает.
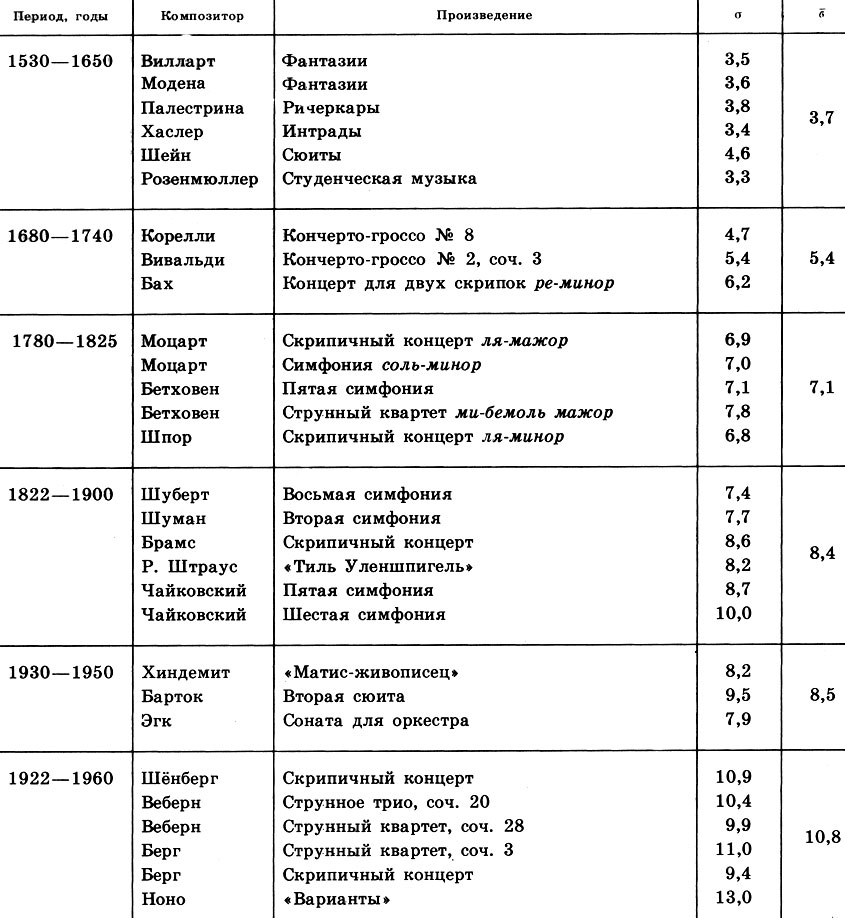
Таблица 4. Усредненные значения о среднего квадратического отклонения высоты звуков музыкального произведения отражают определенный закон развития музыки: за последние 500 лет значение а монотонно возрастает
"Естественно,- отмечал Фукс,- музыковед в связи с нашими распределениями частот может поставить много критически окрашенных вопросов. Так, степень важности партии первой скрипки может быть очень различной в разных частях сочинения: в одной части она может решающим образом определять мелодию, ритм и гармонию, а в других местах сочинения играть роль, в музыкальном отношении подчиненную. Вопросы подобного рода, а также и другие важные обстоятельства должны, естественно, учитываться в тех ветвях музыковедения, которые связаны с количест венными исследованиями". Все это, разумеется, так, и у математического музыковедения непочатый край проблем. Не нельзя не видеть подкупающей простоты и универсальности найденных (пусть простейших) математических закономерностей. Зная эти закономерности, можно, например, подсчитать значение σ для произведения какого-то неизвестного нам автора и, пользуясь данными таблицы 4, отнести это произведение к тому или иному музыкальному направлению. Это будет уже некая "музыкальная криминалистика", построенная на базе математики. В подобной всеобщности и заключается могущество математического метода.
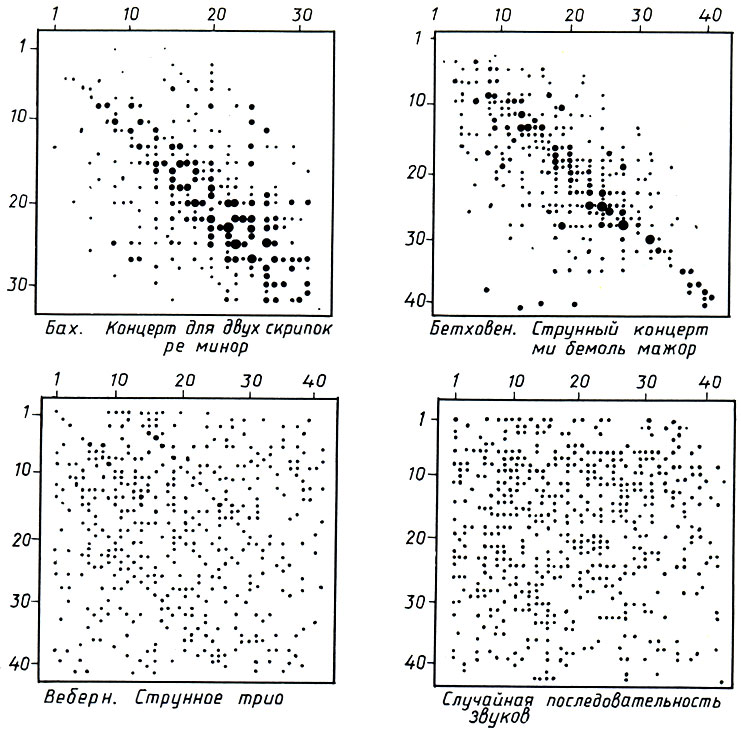
Матрицы переходов в парти первой скрипки (площадь ее ответствующего кружка прс порциональна частоте переход от одного звука к другому). Легко видеть, насколько закономерен характер переходов музыке Баха и Бетховена и насколько он близок к случайному в музыке Веберна
Сделаем еще один, последний, шаг в нашем кратком знакомстве с математическим анализом музыки. Очевидно, что статистические распределения высоты звуков показывают лишь, сколько раз данный звук встречается в музыкальном произведении. Но ведь главным элементом музыки является мелодия - художественно осмысленная последовательность звуков в произведении. Информация же о последовательном расположении звуков в статистическом распределении высот теряется. Получить такую информацию нетрудно с помощью так называемых матриц перехода. Матрица перехода представляет из себя квадратную таблицу, по горизонтальной и вертикальной осям которой отложены все звуки из диапазона звучания музыкального произведения. На пересечении строк и столбцов матрицы перехода ставится частота, с которой в данном произведении совершается переход от одного звука к другому.
На рисунке показаны матрицы переходов, составленные Фуксом, для знакомых нам произведений (взяты партии первой скрипки): концерта для двух скрипок ре-минор Баха, струнного квартета ми-бемоль мажор Бетховена и струнного трио Веберна. Четвертая матрица представляет частоты перехода для случайной последовательности звуков, которая была образована из того же звукового материала, что и сочинение Веберна. Для наглядности частота переходов характеризуется не цифрами, а площадью кружка (чем больше частота перехода, тем больше площадь соответствующего кружка). Простое сопоставление приведенных матриц убеждает в том, насколько строгими и закономерными являются переходы у Баха и Бетховена и насколько они близки к случайным у Веберна. Эти закономерности также можно описать численно с помощью так называемых коэффициентов корреляции, которые служат своеобразной "мерой беспорядка". Для последовательности случайных чисел, т. е. при полном беспорядке, коэффициент корреляции практически равен нулю. Наоборот, при сильной зависимости между элементами коэффициент корреляции близок к единице. В приведенных примерах коэффициент корреляции k для "случайной музыки" равен 0,03 (для трио Веберна й = 0,06), т. е. музыка Веберна близка к "случайной музыке". Напротив, в концерте для двух скрипок Баха k = 0,61, а в струнном квартете Бетховена k = 0,76, т. е. музыка Бетховена является наиболее "закономерной".
Свой анализ матриц перехода Фукс заканчивает следующим замечанием: "Для читателей, интересующихся музыкой, стоит заметить, что из всех возможных переходов используется только небольшая их часть: у Баха 23%, у Бетховена 16% и у Веберна 24% всех возможных связей в рассматриваемом диапазоне звуков. Однако уже из этих простых фактов, к которым можно было бы добавить и другие, вытекает следующее заключение. Возможности музыки, использующей классические инструменты - сочиненной по правилам контрапункта, додекафонной музыки или по каким-нибудь другим правилам,- еще никоим образом не исчерпаны".
Продолжая мысль Фукса, мы можем в заключение сказать, что возможности математических методов анализа музыки и произведений искусства вообще не только не исчерпаны, но представляют собой почти нетронутую целину для исследователя. Экспериментальная эстетика ждет еще своего Ньютона.
строительство заборы из профнастила.
|
ПОИСК:
|
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'