9. Алгебра гармонии - темперация

...Звуки умертвив", 
Музыку я разъял, как труп. Поверил 
Я алгеброй гармонию... 

А. Пушкин

XVIII век в истории музыки начался решительной победой рационализма века Просвещения над антично-средневековым музыкальным целомудрием. К 1700 г. немецкий органист Андреас Веркмейстер (1645-1706) осуществил смелое и гениально простое решение: он отказался от совершенных и несовершенных консонансов - квинт, кварт и терций, оставив в первозданной консонантной красе лишь одну октаву, и попросту разделил ее (геометрически!) на 12 равных частей. В результате пифагорова комма, которую до того времени нетронутой передвигали с места на место, также разделилась на 12 равных частей и стала незаметной. Так в музыке восторжествовала темперация (лат. соразмерность), а новый двенадцатизвуковой строй был назван равномерно-темперированным. Но по порядку...

Вначале, разумеется, были попытки улучшить чистый строй, который сохранял главный недостаток пифагорова строя: невозможность безболезненного перехода из тональности в тональность. Естественным желанием при решении этой проблемы было увеличить количество звуков в октаве. Посмотрим, что из этого выйдет.

Пусть мы настроили октаву в чистом строе от ноты до малой октавы (1) согласно (8.7). Затем повторим ту же процедуру от ноты ре (9/8), для чего 9/8 умножим последовательно на все интервальные коэффициенты чистого строя (нижние цифры в (8.7)). Проделаем эти построения от всех 7 основных нот чистого строя; при этом новые ноты, которые мы будем получать в следующей (первой) октаве, также будем учитывать, ибо у них, разумеется, должны быть октавные повторения в исходной (малой) октаве. В результате наших вычислений получим (новые ноты написаны красным, октавные повторения нот - синим):

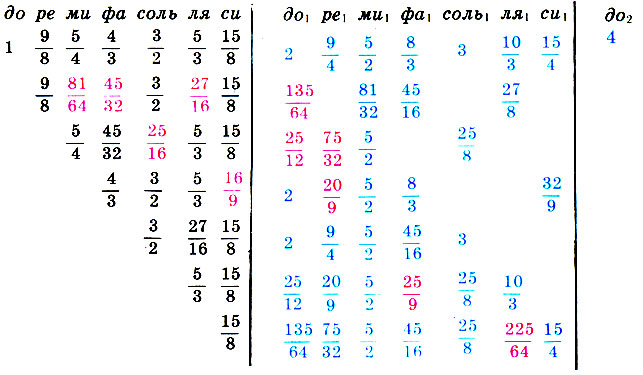
Как видим, 7 основных нот дали нам 11 дополнительных! Итог не слишком радостный. Но процесс образования новых нот все-таки затухает: нота ре дала 4 новых ноты, ми - 3, фа - 2, соль - ни одной (!), ля и си - по одной. Теперь ту же процедуру нужно проделать с новыми одиннадцатью нотами, ибо раз мы хотим сделать все ноты равноправными, то они не должны составлять исключение. Затем - с вновь полученными (самыми новыми) и т. д. К счастью, процесс все-таки замкнется, но какой ценой! В результате получим 84 ступени в октаве! Кто будет играть на столь сложном инструменте?!

Сейчас трудно сказать, кому первому пришла идея равномерно разделить октаву (а вместе с ней и пифагорову комму) на 12 равных частей. Идея эта была подготовлена самой логикой развития музыкального строя и, как говорят в таких случаях, носилась в воздухе. Но изложение этой идеи мы находим опять-таки в энциклопедическом труде Мерсенна "Универсальная гармония". Здесь Мерсенн дал математическое описание нового строя и рассчитал его интервальные коэффициенты. Суть нового метода заключалась в следующем.

Мы знаем, что и пифагоров, и чистый строй не замкнуты, т. е. звук, полученный в результате 12 ходов по квинтам вверх или вниз, не является точным октавным повторением исходного звука, а отличается от него на пифагорову комму. На протяжении столетий наибольшее, что позволяли себе теоретики музыки,- это перегонять комму по гамме с места на место. Комма нетронутой блуждала по гамме и время от времени заявляла о себе в завывании "волков". Так вот, Мерсенн предложил сузить полутона так, чтобы они точно укладывались в октаву. Тем самым он равномерно распределил пифагорову комму по всем 12 полутонам, и она как бы "растворилась" в гамме: стала незаметной.

Для того чтобы разделить октаву (2) на 12 равных частей, в качестве нового полутона необходимо взять по формуле (6.12) интервал 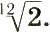Следовательно, математическое выражение равномерно-темперированного строя будет предельно простым:

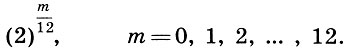(9.1)

Если воспользоваться логарифмическими частотами и логарифмическими интервалами (6.13), т. е. прологарифмировать (9.1) по основанию 2, то математический строй (9.1) примет наиболее простой вид (интервал логарифмической октавы 0≤L≤1 будет арифметически разделен на 12 равных логарифмических полутонов (1/12)):

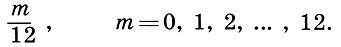(9.2)

Проверим, что будет в новом строе с консонансами и прежде всего с квинтой. Темперированная квинта имеет интервальный коэффициент 2^7/12≈1,4983, который несущественно отличается от интервального коэффициента чистой квинты (3/2):

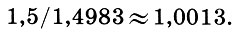
То же справедливо и для кварты (4/3):

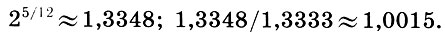
Эти расхождения улавливает лишь изощренный слух профессионала. Несколько хуже обстоят дела с терциями. Сравнивая темперированную большую терцию

2^4/12 = 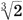1,2599 с пифагоровой терцией (81/64 = 1,2656) и чистой терцией (5/4 = 1,25), имеем 1,2656/1,2599≈1,0044; 1,2599/1,25≈1,008. Как видим, здесь относительные ошибки соответственно в 4 и 8 раз больше, чем для квинты (примерно то же имеем для темперированной малой терции). Но и эти терции в музыкальном отношении вполне приемлемы.

Однако новая система Мерсенна была принята в штыки. Даже приятель Мерсенна по иезуитскому коллежу математик Декарт был возмущен надругательством над чистотой консонансов, а музыкантов, которые рискнут воспользоваться новой темперацией, назвал невеждами, не имеющими никакого представления о законах музыкальной науки. "Что касается Ваших музыкантов,- писал Мерсенну Декарт,- то какими умелыми Вы бы их ни делали, я должен сказать, что они или издеваются, или насмехаются, или никогда ничего не понимали в теории музыки". Чистота звучания и простота целочисленных отношений для консонансов, идущие от родоначальника европейской науки Пифагора, представлялись Декарту нерушимыми. Таким образом, потребовалось еще более полувека, чтобы новая система завоевала себе право на жизнь.

Путь Веркмейстера к равномерной темперации, разумеется, не был усыпан розами. К тому времени и в музыке сформировались два противоборствующих лагеря: теоретики, опиравшиеся в построении музыкальных систем на математику ("разум"), и практики, предпочитавшие полагаться на собственный слух ("ухо"). Любопытно, что среди сторонников "уха" были математики Декарт и Д'Аламбер, а среди сторонников "разума" - композитор Рамо. К счастью, Веркмейстер держался "золотой середины".

Как бы то ни было, но к концу XVII века вышли две его книги, содержавшие практическое изложение равномерной темперации. Первая из них называлась "Музыкальная темперация, или ясное математически правильное изложение того, как при помощи монохорда следует настраивать по хорошей темперации клавиры - органы, позитивы, регали, спинеты, для того чтобы в соответствии с сегодняшней манерой исполнения музыки все тональности звучали в приятной и сносной гармонии. К этому добавлено предваряющее сочинение о преимуществах совершенных и несовершенных музыкальных исчислений, пропорций и консонансов, которые надо учитывать при установлении этой темперации. Наряду с этим приложено гравированное на меди ясное и полное обозначение этой темперации на монохорде. Обнародовано Андреасом Веркмейстером, соборным органистом в Кведлинбурге. 1691 год". Название второй книги мы лучше опустим.

Итак, к началу XVIII века органы, настроенные Андреасом Веркмейстером, зазвучали в равномерно-темперированном строе. Преимущества нового строя были очевидны. Это был замкнутый энгармонический строй, состоящий из интервалов, вполне приемлемых для музыкального слуха и в гармоническом, и в мелодическом исполнении. В новом строе стали совершенно безболезненными переходы из тональности в тональность (модуляции), "волки" навсегда покинули орган. Простота нового строя также была его неоспоримым преимуществом.

Конечно, и в век Просвещения новое не всеми воспринималось восторженно. Выдающийся немецкий композитор Георг Фридрих Гендель (1685-1759) не принял новшества. Отказ от совершенных консонансов возмущал его. К счастью, равномерная темперация нашла сторонника в лице сверстника Генделя, великого немецкого композитора и органиста Иоганна Себастьяна Баха (1685-1750). В простоте и математической строгости равномерной темперации Бах гениально предвидел подлинный путь развития музыки. Предвидения Баха сбылись: равномерная темперация сегодня лежит в основе всей мировой музыки.

Иоганн Себастьян Бах (1685- 1750). Последний прижизненный портрет И. С. Баха работы неизвестного художника

Для демонстрации возможностей нового строя Бах написал свое бессмертное произведение "Хорошо темперированный клавир", основной целью которого было ознакомить играющих на клавире со всеми двадцатью четырьмя (12-мажорными и 12-минорными) тональностями хроматической гаммы нового "хорошо согласованного" строя. Бах хотел показать равноценность всех тональностей при новой системе настройки клавира и вместе с тем выявить характерную окраску каждой тональности. На титульном листе "Хорошо темперированного клавира" значилось: "Для пользы и употребления жадного до учения музыкального юношества, как и для особого времяпрепровождения тех, кто уже преуспел в этом учении, составлено и изготовлено Иоганном Себастьяном Бахом - в настоящее время великокняжеским Ангальт-Кетенским капельмейстером и директором камерной музыки. В году 1722".

Разумеется, Бах слишком скромно оценивал свое произведение. Цикл прелюдий и фуг Баха занимает особое место в мире музыки. Это не просто один из бессмертных шедевров мировой музыки. Это настоящая энциклопедия полифонического искусства, его альфа и омега, настольная книга каждого мыслящего музыканта. Не случайно Бетховен называл "Хорошо темперированный клавир" своей "музыкальной библией", которую он изучал с раннего детства до глубокой старости. Да и сам Бах всю жизнь обращался к своему детищу и через 24 года написал вторую часть "Хорошо темперированного клавира", также состоящую из 24 прелюдий и фуг.

И все-таки является ли 12-звуковая равномерная темперация "абсолютной истиной" в музыке? Разумеется, нет! Спор Баха и Генделя продолжается. Музыкантов с особо тонким слухом раздражают "тупые" консонансы темперированного строя. Чайковский после отдыха на природе болезненно ощущал недостатки темперированной музыки, и прежде всего собственной. Известно, как мучился Скрябин, не находя в рояле чистых интервалов. В последние годы жизни Скрябин пытался сконструировать рояль с дополнительными тонами, но неожиданная смерть не позволила осуществить задуманное. Наш соотечественник и современник, крупнейший пианист XX века Святослав Рихтер признается, что он физически старается преодолеть темперацию рояля при помощи звукоизвлечения, придавая диезным и бемольным звукам, когда это нужно, различную тембровую окраску. Поиски новых равномерных темперации продолжаются. Разработаны 24-, 48- и 53-зву-ковые равномерные темперации. На каждую из них специально написана музыка и сконструированы музыкальные инструменты. Но все они практического распространения не получили. Возможно, новые темперации ждут еще нового Веркмейстера и нового Баха...

На этом можно было бы поставить точку. Но мы поставили многоточие, ибо у вдумчивого читателя должен возникнуть еще один вопрос: почему все-таки октава разделена именно на 12 частей? Это вопрос из области математики, и ответ на него содержится в решении задачи, которую мы сформулируем так.

Требуется разделить интервал октавы 1≤f≤2 на n геометрически равных частей 1 = f₀≤f₁≤f₂≤...≤f_n = 2, так, чтобы k-я точка деления приходилась на главный консонанс октавы - квинту, т. е. f_k = 3/2 (0<k<n). Так как согласно (6.12) f_k = 2^k/n, то мы приходим к уравнению

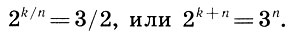(9.3)

Но левая часть уравнения (9.3) есть число четное при любых n и k, тогда как правая - число нечетное. Таким образом, мы пришли к противоречию, которое доказывает, что уравнение (9.3) в целых числах решений не имеет. Одновременно мы можем сделать важный вывод: шкала равномерно-темперированного строя никогда точно не пройдет через квинту.

Будем искать в целых числах приближенные решения уравнения (9.3). Логарифмируя, представим это уравнение в виде

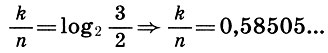(9.4)

и, как говорят математики, найдем рациональные приближения иррационального числа 0,58505... Такие задачи в математике решаются с помощью цепных дробей, т. е. дробей вида

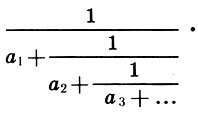(9.5)

Здесь a₁, а₂, а₃, ... - натуральные числа. Известно, что всякое число а∈[0; 1] можно разложить в цепную дробь (9.5), которая будет бесконечной, если число а иррациональное. Рациональные выражения

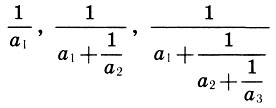
и т. д.

называются подходящими дробями цепной дроби (9.5), т. е. являются рациональными приближениями числа а.

Разложим число 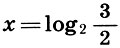в цепную дробь. По определению логарифма имеем

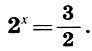(9.6)

Ясно, что х<1. Положим 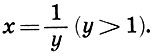Тогда (9.6) примет вид

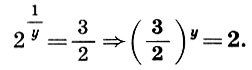(9.7)

Легко видеть, что 1<y<2,так как при этом

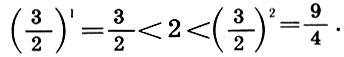
Поэтому положим

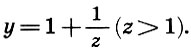
Уравнение (9.7) преобразуется к виду

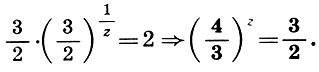(9.8)

Очевидно, что 1<z<2, так как 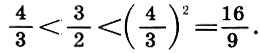Следовательно, полагаем

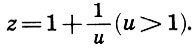
Тогда уравнение (9.8) примет вид

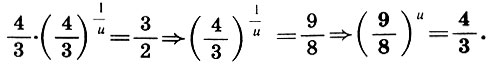(9.9)

Так как 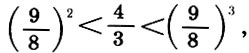, то для u получаем оценку 2<u<3. Поэтому в (9.9) делаем подстановку 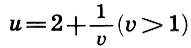и получаем

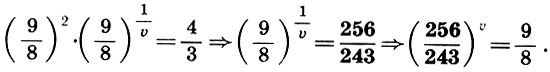(9.10)

С помощью таблиц логарифмов или простой проверкой на микрокалькуляторе находим оценку для v:2<u<3. Наконец, сделаем еще одну замену 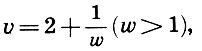отчего (9.10) примет вид

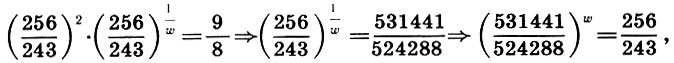
или

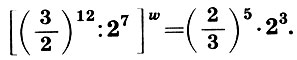(9.11)

Для w справедлива оценка 3<w<4, поэтому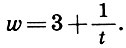

Не будем более испытывать терпение читателей (процесс разложения иррационального числа в цепную дробь все равно бесконечен). А в качестве компенсации за длинные выкладки обратим внимание на то, что в наших приближениях (9.6) - (9.11) все время фигурируют музыкальные интервалы: октава (2), квинта (3/2), кварта (4/3), тон (9/8), полутон (256/243) и даже пифагорова комма ((3/2)12:27)!

Построим теперь соответствующую цепную дробь:

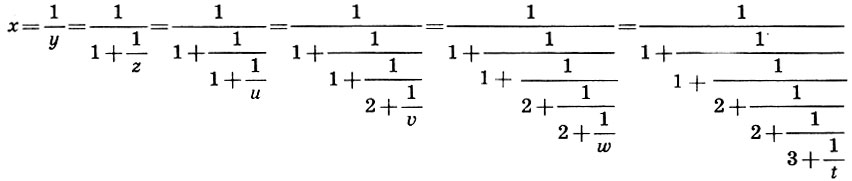
и выпишем подходящие дроби:

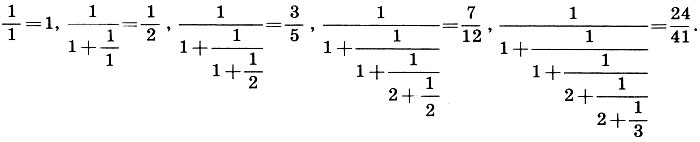
Первые три дроби 1; 0,5; 0,6 дают слишком грубое приближение к числу x = 0,58505... Четвертая дробь k/n = = 7/12 = 0,5833... является достаточно хорошим приближением. Она-то и положена в основу 12-звукового равномерно-темперированного строя (n = 12, k = 7, т. е. на седьмой ступени 12-звуковой гаммы находится темперированная квинта). Пятая дробь 24/41=0,58536 дает еще лучшее приближение. Таким образом, мы получаем еще одну равномерную темперацию, которая на 24-й ступени имеет практически идеальную квинту. Но ведь октава при этом делится на 41 ступень! Вряд ли кто отважится играть на столь сложном инструменте. Итак, именно 12-звуковая темперация является той "золотой серединой", которая обеспечивает достаточно чистое звучание консонансов при достаточной простоте музыкальной гаммы.

История создания равномерной темперации свидетельствует о том, как тесно порой переплетаются судьбы математики и музыки. Равномерная темперация в музыке появилась вслед за изобретением логарифмов и развитием алгебры иррациональных величин в математике. Без знания логарифмов провести расчеты равномерно-темперированного строя (8.8) было бы попросту невозможно. Логарифмы стали той "алгеброй гармонии", на которой выросла темперация.

И в заключение скажем несколько слов об одном любопытном и пока загадочном свойстве равномерной темперации. Согласно логике построения темперированной шкалы (9.1) все 12 мажорных, равно как и все 12 минорных, тональностей равномерно-темперированного строя должны звучать одинаково. Однако музыканты считают, что каждая тональность темперированного строя обладает своей неповторимой окраской. Так, композиторы единодушно сходятся в том, что до мажор характерен для светлого, солнечного настроения. Очень любил до мажор за жизнерадостность и оптимизм Бетховен. Вспомним 1-ю Симфонию и 1-й Концерт для фортепиано с оркестром Бетховена, написанные в до мажоре, которые как бы радостно перекликаются друг с другом; или его же 21-ю Сонату до мажор, названную за светлые и прозрачные тона именем богини утренней зари Авроры. Считается, что ми мажор выражает взволнованное, напряженное, мятущееся настроение. Поэтому именно ми мажор был так созвучен восторженной, страстно ищущей и терзаемой противоречиями душе Листа; в ми мажоре Листом написаны многие фортепианные произведения, транскрипции, "Фауст-симфония". В тональности фа диез мажор композиторы находят легкое, радостно возвышенное, романтическое настроение, столь характерное для творчества Шопена ("Баркарола", Экспромт соч. 36, Ноктюрн № 2 соч. 15). До минор считается тональностью мужественной печали, героико-трагических образов (вспомним огненный пафос "Патетической" сонаты Бетховена, знаменитый "революционный" этюд Шопена или шквальные кульминации 2-го Концерта для фортепиано с оркестром Рахманинова); ми бемоль минор - тональность глубоко трагических состояний. Например, Полонез № 2 соч. 26 - одно из самых скорбных творений Шопена.

Мы не можем сказать, отражают ли такого рода суждения какие-либо неизвестные пока объективные закономерности, или это дань устоявшейся традиции. Если мы имеем дело с традицией, то ее корни следует искать в пифагоровом строе. Действительно, в пифагоровом строе энгармонические звуки не только нетождественны, но и принципиально отличаются друг от друга по своим качествам и выразительности. В пифагоровом строе соль диез, например, находится на пифагорову комму выше, чем ля бемоль. Поэтому соль диез тяготеет к верхнему звуку ля и воспринимается светлее, чем ля бемоль, который направлен к нижнему звуку соль и потому кажется более мрачным. Следовательно, и все повышенные звуки восходящей линии квинтового ряда (диезные звуки) имеют светлый характер, тогда как пониженные (бемольные) звуки нисходящей линии квинтового ряда (см. (8.2)) несут мрачный оттенок. Итак, все та же пифагорова комма окрашивает бемольные и диезные звуки в противоположные цвета - темные и светлые. Теперь становится понятным, почему Шопен написал свой знаменитый траурный марш из 2-й Сонаты соч. 35 в си бемоль миноре - тональности с пятью бемолями, а "Баркаролу" - самое утонченное и поэтическое из своих произведений, ставшее символом интимной лирики в музыке,- в фа диез мажоре - тональности с шестью диезами. Вот почему похоронный марш из 12-й Сонаты написан Бетховеном в ля бемоль миноре - тональности с наибольшим числом, семью бемолями, хотя, по мнению знатоков, эта находка Бетховена во многом теряет в равномерно-темперированном строе фортепиано.

Так что же такое есть индивидуальная окраска тональностей: традиция, идущая от пифагорова строя, или неизвестная объективная закономерность? Окончательного ответа на этот вопрос пока не существует.

Вот так, вместо обещанной точки в конце параграфа мы вновь пришли к вопросительному знаку. Но ведь это и хорошо, ибо новые вопросы зовут нас в новые пути в неизвестное! А впереди у нас, пожалуй, главный вопрос всей второй части: в чем секрет "закона Пифагора"? Почему приятные для "уха" консонансные интервалы математически выражаются такими приятными для "разума" простыми целочисленными соотношениями 2/1, 3/2, 4/3, 5/4, 6/5?