
7. "Космическая музыка": от Платона до Кеплера
Современник, даже когда его влечет старина, склонен считать своих предков людьми простодушными и недалекими. Он замечает в них прежде всего то, чего им не хватало с современной точки зрения, и обычно не замечает того, чего ему самому не хватает по сравнению с ними.
В наш бурный век космической тематикой вряд ли кого удивишь, тем более читателей, родившихся во время полетов человека в космос. "Космическая музыка" - это нечто вибрирующее, электронное из фильмов о летающих тарелках и инопланетянах - тоже стала привычной. Но вот то, что задолго до нашей эры, во времена, когда человечество "летало" только на восковых крыльях в мифах о Дедале и Икаре, была своя "космическая музыка", многим, возможно, покажется удивительным.
По преданию, слово "космос", первоначально означавшее прекрасно устроенный, ввел в обиход Пифагор. "Скажи мне, ...разве есть что-либо стройное и прекрасное, что не было бы подражанием миру. Отсюда имя "Космос", которое греки дали ему",- вторил Пифагору через полтысячелетия Апулей. Из античности термин "космос" перешел в современную науку как синоним слова "вселенная".
Итак, космос для пифагорейцев - это гармоничное, пропорциональное строение мира. Сами же пропорции, как мы уже видели, мыслились греками музыкально" поэтому и весь космос оказывался гармонично устроенным и музыкально звучащим телом. Согласно пифагорейским представлениям, планеты располагались на небесных сферах и совершали вместе с ними круговое вращение. Тогда, как и все движущиеся тела, вследствие трения об эфир они издавали звуки, которые соединялись в музыкальные созвучия. Так Рождалась чудесная музыка - "мировая Музыка", или "гармония сфер", без коброй мир бы распался. Сама же музыка - это первое из искусств, доставляющих людям радость,- являлась, по их Мнению, отражением гармонии, царящей сРеди небесных сфер.
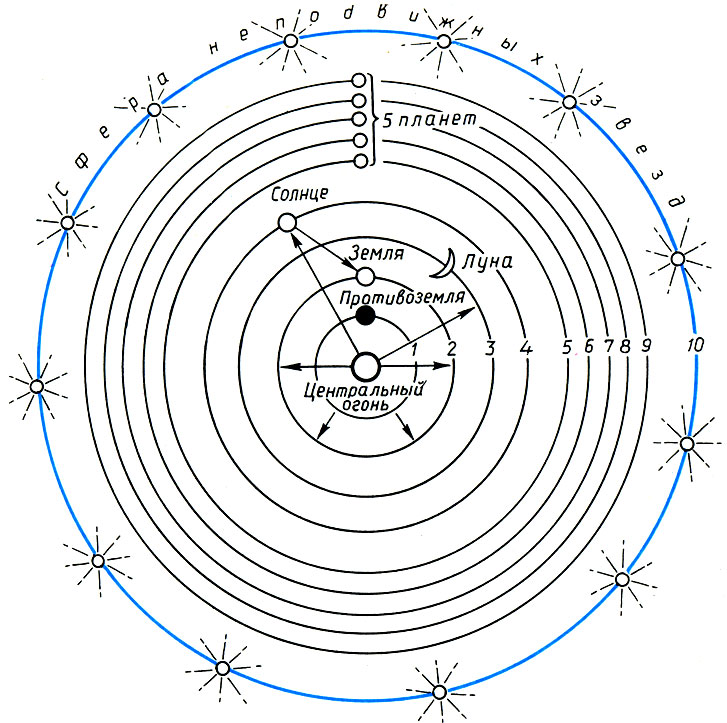
Система мира по Филолаю
Учение о музыке сфер - самый туманный и вместе с тем поэтичный мотив пифагорейской эстетики. Он имел тысячи вариантов, оттенков и тысячелетнюю традицию, начиная от Пифагора и Платона до "Гармонии мира" Иоганна Кеплера, написанной уже в XVII веке. Разумеется, учение о "космической музыке" для нас, современников космических полетов, не более как красивая сказка, и расскажем мы эту сказку, чтобы показать, насколько сильным было музыкальное начало во всем античном мировоззрении. Кроме того, как и во всякой сказке, в этом учении рассыпаны зерна истины, позволяющие увидеть глубокие параллели в развитии человеческой мысли.
Первое письменное изложение пифагорейских идей появилось около 420 г. до н. э. в сочинении "О природе". "Природа, сущая в космосе, гармонично слажена из беспредельного и определяющих начал. Так устроен весь космос и все, что в нем" - так начинается эта книга, приписываемая Филолаю, ученику непосредственного ученика Пифагора - Гиппаса. Здесь же мы находим и первое письменное свидетельство о музыкально-числовом строении космоса.
По Филолаю, центром мироздания является некий Центральный Огонь, вокруг которого на десяти концентрических сферах в порядке удаления от него вращаются так называемая Противоземля, затем Земля, Луна, Солнце, пять планет (Меркурий, Венера, Марс, Юпитер, Сатурн - их последовательность Филолаем не указана)* и, наконец, Сфера неподвижных звезд. Центральный Огонь и Противоземля невидимы, ибо заслонены поверхностью Земли. Солнце, по Филолаю, только отражает свет и тепло Центрального Огня. Противоземля же введена им отчасти для объяснения солнечных затмений, отчасти для достижения требуемой числовой мистикой "священной десятки" - вместе с Противоземлей сфер получается десять. В пифагорейской системе Земля не является центром мироздания, а вместе с другими планетами движется вокруг Центрального Огня - прообраза Солнца. Вот почему, когда в XVI веке церковь развернула борьбу с гелиоцентрическим учением Коперника, это учение именовалось пифагорейским.
* (Напомним, что остальные три планеты Солнечной системы - Уран, Нептун и Плутон - были открыты лишь в XVIII, XIX и XX веках соответственно. )
Внутреннее устройство пифагорейского космоса напоминало своеобразную музыкальную шкатулку: каждая из десяти движущихся сфер издавала некоторый звук. "Когда несутся Солнце, Луна и еще столь великое множество таких огромных светил со столь великой быстротою, невозможно, чтобы не возникал некоторый необыкновенный по силе звук",- утверждает неизвестный пифагорейский автор возможно Филолай. Высота звука определялась скоростью движения сферы, зависящей от расстояний между сферами, а последние находились в той же пропорции, что и интервалы музыкальной гаммы. Таким образом, колеблемый движением сфер эфир издает чудесную мировую музыку. Однако человеческое ухо не слышит этой ни с чем не сравнимой музыки. Как рожденный на берегу моря человек перестает в конце концов различать беспрестанный рокот волн, так и слух человека привык и не замечает гармонического звучания небесных сфер.
Итак, согласно пифагорейцам, небесная музыка изначально незримо живет в человеке. Вот почему человеческая душа охотно откликается на обычную земную музыку, которая является лишь подражанием небесной; вот почему из всех искусств музыке в античности отводилась исключительная роль.
В своем конспекте гегелевской "Истории философии" В. И. Ленин по поводу пифагорейского учения отмечает "связь зачатков научного мышления и фантазии &##225; lа религии, мифологии" (т. 29, с. 225). Особое внимание В. И. Ленин уделяет пифагорейскому учению о гармонии сфер, подчеркивая, что здесь имеется "намек на строение материи!" (т. 29, с. 224).
Дальнейшее развитие пифагорейское учение о гармонии сфер получило в трудах Платона. Платоновский диалог "Тимей", эта квинтэссенция древнего пифагорейства, является лучшим образцом античной космологии. Однако многое в "Тимее" изложено туманными и заумными намеками. Уже в древности эти места вызывали бесконечные споры, разночтения и комментарии, которые длятся и до сего времени.
Платон исходит из геоцентрической системы космоса: центром мироздания Для него является неподвижная Земля, вокруг которой на семи сферах* вращаются Луна, Солнце, Венера, Меркурий, Марс, Юпитер, Сатурн. Далее следует сФера неподвижных звезд. Как видим, несостоятельность Центрального Огня и Противоземли ко времени Платона была Уже осознана.
*(Отсюда пошло выражение "Быть на седьмом небе", обозначающее высшую степень блаженства.)
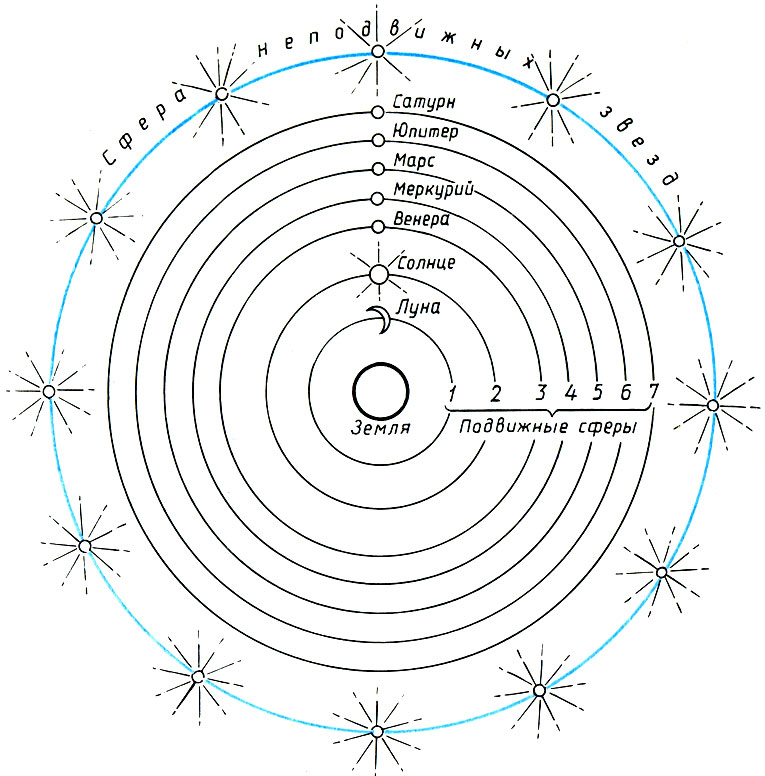
Система мира по Платону
На базе этой системы мироздания Платон развивает теорию небесного гептахорда - семиструнника, т. е. теорию семи подвижных сфер, настроенных в музыкальных отношениях. Согласно Платону, творец Вселенной - Демиург, создав вещество Вселенной, разделил его на две части: одна часть пошла на построение сферы неподвижных звезд, а вторая была математически строго разделена на семь частей для образования сфер Луны, Солнца и пяти планет. По этому поводу в "Тимее" Платона мы читаем: "Делить же он начал следующим образом: прежде всего отнял от целого одну долю, затем вторую - вдвое большую, третью - в полтора раза больше второй и в три раза больше первой, четвертую - вдвое больше второй, пятую - втрое больше третьей, шестую - в восемь раз больше первой, а седьмую - больше первой в двадцать семь раз". В результате получился ряд чисел
1 2 3 4 9 8 27, (7.1)
описывающий гармонию небесных сфер, или небесный гептахорд. Однако ни порядок расположения сфер, несущих светила, ни порядок отсчета чисел в ряде (7.1) Платоном указан не был. Поэтому на протяжении последующих двух тысячелетий члены платонова гептахорда имели самую разнообразную физическую интерпретацию.
Самым простым и соблазнительным было трактовать числа (7.1) как относительные расстояния от Земли до Луны, Солнца, Венеры, Меркурия, Марса, Юпитера и Сатурна соответственно. Тогда эти числа представляли и относительные высоты тонов, так как высота тона, издаваемого сферой, мыслилась пропорциональной скорости вращения сферы, а скорость вращения - пропорциональной расстоянию до неподвижной Земли. Таким образом, чем дальше находилась планета от Земли, тем больше была ее скорость и тем выше издаваемый ею тон. Скорее всего, эти рассуждения были навеяны простым опытом: камень, раскручиваемый на веревке, со свистом разрезает воздух и прекрасно демонстрирует все описанные закономерности. Правда, при такой трактовке относительное расстояние до Марса (9) получалось больше, чем до Юпитера (8), и, чтобы "исправить" эту ошибку, числа 9 и 8 в (7.1) просто переставили. Вот почему во многих текстах платонов гептахорд фигурирует в искаженном виде: 1, 2, 3, 4, 8, 9, 27.
И все-таки оставалось непонятным: откуда вообще взялся этот странный ряд чисел? Это загадка, которую исследователи, начиная с Аристотеля, чаще всего трактовали как некий курьез, если не просто глупость, не требующую даже разъяснений. "Однако,- как справедливо замечал А. Ф. Лосев,- такой антиисторический подход не может быть у современного исследователя, который, конечно, настолько далек от древнего пифагорейства, что даже не испытывает потребности его критиковать, а должен рассмотреть его со всеми объективно-историческими причинами, делающими его существование понятным".
Ключ к Платонову гептахорду, по-видимому, спрятан в самом пифагорейском понимании числа, а именно: единицы - как символа неделимого начала, двойки - как символа неопределенной бесконечности и тройки - как символа определенности. Но для Платона это слишком просто, и в качестве символа беспредельности он берет куб со стороной 2. Тогда его геометрические параметры (длина, площадь грани и объем) дают числа 2, 4, 8. А в качестве символа определенности Платон берет куб со стороной 3 и параметрами 3, 9, 27. Тогда взаимное переплетение этих двух троек чисел плюс начало всего - единица - и дают то единство "беспредельного и определяющих начал", о которых говорил Филолай.
Интересную реконструкцию платонова космоса совсем недавно, в 1985 г., предложил инженер С. В. Житомирский. Учитывая, что небесные сферы мыслились Платоном материально, т. е. обладали некоторой толщиной (такое представление сохранилось вплоть до Кеплера), Житомирский трактует числа (7.1) как толщины соответствующих сфер, причем отсчет начинает не от Земли, как это всегда было принято, а, наоборот, от сферы неподвижных звезд. Далее, вспоминая, что на изготовление последней сферы пошло столько же материала, сколько и на все
остальные, он полагает толщину сферы неподвижных звезд равной толщинам всех остальных сфер, т. е. 54 = 1 + 2 + 3 + 4 + 9 + 8 + 27. Таким образом получается реконструкция картины платонова космоса, которая согласуется с другими космологическими текстами Платона, а числа гептахорда (7.1) наполняются конкретным геометрическим содержанием:

Земля - Луна - Солнце - Венера - Меркурий - Марс - Юпитер - Сатурн - Небо звезд
Заметим, что и реконструкция Житомирского также страдает изъяном, так как Земля теперь растворилась в сфере Луны. Не будем более погружаться в бездну вопросов Платонова космоса, из которых уже два с половиной тысячелетия ищут выхода, и перейдем к музыкальной стороне учения Платона. Легко видеть, что платонов гептахорд содержит в себе все основные музыкальные интервалы: октаву (2/1), квинту (3/2), кварту (4/3), тон (9/8) и полутон 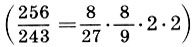 . Объясняется это просто, ибо, как мы увидим в следующей главе, все тона пифагоровой гаммы получаются ходами вверх или вниз по квинтам (3/2), а квинта составлена из отношения тройки и двойки, т. е. из тех чисел, что и платонов гептахорд. С помощью полученных интервалов можно рассчитать строй любого лада. Неудивительно, что Платон утверждает, будто космос настроен в дорийском ладу, этом истинно национальном ладу древних греков, хотя остается непонятным, как получить строй дорийского лада из Платонова гептахорда. Не очень ясно также и то, что на самом деле представляет собой звучание Платонова гептахорда: гармонию или дисгармонию или даже какофонию сфер. Попробуйте решить для себя этот вопрос сами, сыграв гептахорд (7.1), скажем, от ноты До большой октавы: До-до-соль-до1-ре2-до2-ля3.
. Объясняется это просто, ибо, как мы увидим в следующей главе, все тона пифагоровой гаммы получаются ходами вверх или вниз по квинтам (3/2), а квинта составлена из отношения тройки и двойки, т. е. из тех чисел, что и платонов гептахорд. С помощью полученных интервалов можно рассчитать строй любого лада. Неудивительно, что Платон утверждает, будто космос настроен в дорийском ладу, этом истинно национальном ладу древних греков, хотя остается непонятным, как получить строй дорийского лада из Платонова гептахорда. Не очень ясно также и то, что на самом деле представляет собой звучание Платонова гептахорда: гармонию или дисгармонию или даже какофонию сфер. Попробуйте решить для себя этот вопрос сами, сыграв гептахорд (7.1), скажем, от ноты До большой октавы: До-до-соль-до1-ре2-до2-ля3.
Впрочем, все это сегодня уже неважно. Для нас, людей XX века, важно другое: Платон мыслит мировое пространство неоднородным, как неодинаково натянуты струны единого музыкального инструмента. Но ведь эта мысль о неоднородности мирового пространства созвучна выводам из общей теории относительности Альберта Эйнштейна об искривленности пространства - времени и его неоднородности! Более двух тысячелетий, от Платона до Эйнштейна, мировое пространство мыслилось абсолютным и однородным! И вот за этот огромный промежуток времени, практически равный всей истории европейской цивилизации, наука, как и определено законами диалектики, совершает огромный виток по спирали и прежний вывод делается на базе самых современных научных знаний, а старая научная платформа кажется наивной и смешной! Сколько еще таких витков предстоит сделать науке?!
От внешнего строения космоса Платон в "Тимее" переходит к внутреннему его строению, т. е. строению материи. Это знаменитое учение Платона о четырех стихиях - основных компонентах мира и их атомах - Платоновых телах. Менее известно, что это учение также "музыкально", но, прежде чем остановиться на нем, следует сказать несколько слов о самом Платоне и его научных взглядах, что, видимо, поможет понять истоки этого экзотического учения.

Платон (427-347). Римская мраморная копия с греческого оригинала. Ок. 370 до н. э
Платон (427-347 гг. до н. э.) - величайший философ античности, оказавший огромное влияние на развитие всей мировой культуры. Однако Платон был не только философом, создателем первой в истории человечества системы объективного идеализма, "линии Платона", по определению В. И. Ленина (т. 18, с. 131), но также и блестящим художником слова, организатором и теоретиком науки, ученым и гражданином города-государства Афины. После казни своего любимого учителя Сократа, болезненно переживая кризис афинской демократии, Платон покинул Афины и около двенадцати лет провел в путешествиях. Вернувшись на родину, Платон основал научную школу - Академию, которая разместилась на купленном для этой цели Платоном участке в роще близ Афин. Роща носила имя древнеаттического героя Академа, откуда и пошло название первой в истории человечества научной школы - Академии.
Платон и его ученики, платоники, были самой влиятельной после пифагорейцев группой мыслителей, а Платонова Академия в течение девяти столетий оставалась центром, влекущим к себе лучшие умы античности. Платон направлял и воодушевлял научную работу. Великие математики Теэтет и Евдокс были друзьями Платона, его учителями в математике и учениками в философии. Великий ученик Платона - Аристотель, будущий учитель и воспитатель Александра Македонского, двадцать лет жизни провел в благотворной атмосфере Академии. Хотя сам Платон и не был математиком, он придавал огромное значение изучению математики, живо интересовался ею и требовал от своих учеников основательных знаний математики, прежде чем посвятить их в свою философию. По преданию, на вратах Академии Платона было начертано: "Негеометр да не войдет!", а одному из начинающих философов, не знавшему математики, Платон сказал: "Уйди прочь! У тебя нет орудия для изучения философии..."
Не останавливаясь на философской системе Платона, отметим только, что, согласно Платону, существуют два мира: материальный несовершенный мир вещей и совершенный мир идей. Законы мира вещей несовершенны и преходящи, тогда как в мире идей господствуют абсолютные и неизменные истины, которые и надлежит изучать философу. Материальный мир есть не более как одна из несовершенных реализаций мира идей, и постигнуть реальный мир можно только с помощью математики идеального мира. То, что идеальный мир основан на математике, сомнений не вызывало. "Знание, к которому стремятся геометры, есть знание вечного, а не того, что тленно и преходяще",- утверждал Платон.
Таким образом, Платон ясно осознавал значение математизации науки, и это именно тот путь, по которому пошло развитие науки в античности и по которому оно продолжает идти сегодня. Однако следует четко различать: то, что Платон видел в математике инструмент познания законов природы, безусловно, верно, но что он считал истинным только мир идей, ложно. Это заблуждение Платона было вызвано тем очевидным фактом, что законы мира вещей открывались лишь путем абстрагирования и идеализации, путем "стирания случайных черт". Потому идеальный мир идей и казался Плауну истинным и непреходящим. Таким образом, идеализм Платона был связан с преувеличением роли разума и недооценки значения опыта.
Показательно, что в наше время стремительной математизации и широчайшего применения ЭВМ, время, когда стало возможным физический эксперимент заменить экспериментом вычислительным и буквально "увидеть" на экране дисплея ЭВМ то или иное физическое явление, некоторые философы-идеалисты пытаются поднять на щит учение Платона. Ответим сформулирован в статье Ю. А. Жданова "Философские проблемы современного естествознания": "В законах математики отражаются не свойства ума, а свойства всей материи, в том числе и ума. Вот почему эти законы имеют объективное содержание, вот почему они обладают эвристическим характером, вот почему на их основе можно строить научный прогноз и предсказание, проверяя их в последующем практикой". Напомним, что и в начале нашего столетия - времени рождения теории Эйнштейна и бурных потрясений в физике - Философы-идеалисты восклицали: "Материя исчезла, остались одни уравнения!" В. И. Ленин в своем труде "Материалы и эмпириокритицизм" подверг резкой критике эту идеалистическую трактовку математического знания, а гениальное ленинское предвидение "Электрон так жe неисчерпаем, как и атом" (т. 18, с. 277) подтверждается всем ходом развития физики элементарных частиц.
Но вернемся в Древнюю Грецию. Теперь нам будет понятно, откуда Платону пришла мысль отождествлять физические элементы (атомы четырех стихий) с геометрическими телами - правильными многогранниками: в геометрии Платон видел ключ к познанию природы. Впрочем, по порядку...
Многогранник называется правильным, если он лежит по одну сторону от плоскости любой его грани, т. е. является выпуклым, и все его грани есть равные правильные многоугольники. Простой подсчет суммы углов при вершине правильного многогранника показывает, что существует только пять правильных многогранников*. Доказательство этого факта имеется в XIII книге "Начал" Евклида, но сам факт был, безусловно, известен Платону, а правильные многогранники знали пифагорейцы задолго до Платона. Форму правильных тел, по-видимому, подсказала древним грекам сама природа: кристаллы поваренной соли имеют форму куба, кристаллы квасцов - октаэдра, а кристаллы пирита - додекаэдра. Последний, как показали раскопки в итальянских Альпах, был любимой игрушкой этрусских детей задолго до нашей эры.
* ( В самом деле, сумма плоских углов s при вершине выпуклого многогранника должна быть строго меньше 360°, а число граней при вершине m≥3. Тогда гранями правильного многогранника могут быть только три плоские фигуры: правильные треугольник, четырехугольник (квадрат) и пятиугольник, ибо уже для шестиугольников s = 120°*3 = 360°. Название правильному многограннику дается по общему числу граней М. Таким образом, из равносторонних треугольников можно составить три правильных многогранника при m = 3, 4, 5 (при m = 6 s = 60°*6 = 360°):
1. Тетраэдр (четырехгранник): m = 3, М = 4.
2. Октаэдр (восьмигранник): m = 4, М = 8.
3. Икосаэдр (двадцатигранник): m = 5, М = 20, а из квадратов и правильных пятиугольников - только по одному при m = 3 (при m = 4 s = 90°*4 = 360° - для квадратов и s = 108°*4 = 432° - для пятиугольников).
4. Гексаэдр (шестигранник), или куб: m = 3, М = 6.
5. Додекаэдр (двенадцатигранник): m = 3, М = 12.
В любом выпуклом многограннике числа вершин L, граней М и ребер N связаны формулой Эйлера L + M - N = 2.)
Правильные многогранники всегда восхищали пытливые умы симметрией, простотой и мудростью своих форм. Леонардо да Винчи любил изготовлять из дерева каркасы правильных тел и преподносить их в виде подарка различным знаменитостям. К сожалению, мы не можем подробнее остановиться на массе любопытных геометрических свойств и физических приложений правильных тел. это выходит за рамки нашего разговор* а тем, кто заинтересуется ими, мы рекомендуем прочитать книгу К. Левитил "Геометрическая рапсодия".
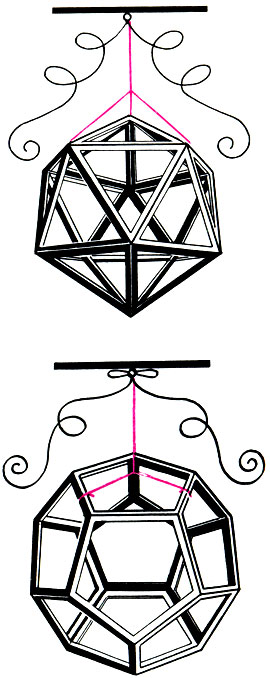
Рисунки тел Платона, выполненные Леонардо да Винчи к книге Луки Пачоли 'О божественной пропорции'. Венеция. 1509
Ко времени Платона в античной философии уже созрела концепция четырех элементов (стихий) - первооснов материального мира: огня, воздуха, воды ц земли. Огонь и землю Платон считает основными компонентами для образования космоса: "...всему, что имело произойти, надлежало, конечно, быть телесным, видимым и осязаемым. Но быть видимым ничто не может без посредства огня, точно так же и осязаемым ничто не может быть без чего-нибудь твердого, твердым же ничто не может быть без земли (Тимей)". Между основными стихиями помещаются две средние - вода и воздух, и все они связываются музыкальными отношениями. Атомам земли Платон придает форму куба, так как и земля, и куб отличаются неподвижностью и устойчивостью. Атомам воды - форму икосаэдра, так как вода отличается текучестью, а из всех правильных тел икосаэдр - наиболее "катящийся". Атомам воздуха - форму октаэдра, ибо воздух движется взад и вперед и октаэдр как бы направлен одновременно в разные стороны. Атомам огня - форму тетраэдра как наиболее острого, мечущегося в разные стороны. Не у дел остался пятый правильный многогранник - додекаэдр. Для него Платон вводит пятый элемент - "пятую сущность"* - мировой эфир, атомам которого придается форма додекаэдра как наиболее близкого к шару - самому с0' вершенному по форме телу. С тех пор правильные многогранники называются также платоновыми телами.
* (Пятая сущность - по-латыни квинтэсенция - у средневековых алхимиков ста означать тончайший элемент, составляющий якобы сущность вещей. В настоящее время квинтэссенция - синоним самого главного, иболее существенного.)
Далее, поскольку в музыкальных отмщениях греки видели основу "всеобщей гармонии", Платон устанавливает эти отношения не только для космических тел (гармония сфер), но и для самих элементов, из которых состоит космос. По Платону, отношение основных элементов - атомов земли к атомам огня - равно октаве (2/1), отношение атомов земли и воды, а также воздуха и огня равно кварте (4/3) и т. д. Несмотря на любовь Платона к геометрии, эти отношения не имеют никакой математической базы. Ими Не связаны ни число вершин Платоновых тел, ни объемы этих тел, вписанных одно в другое, ни число ребер или граней.
Заметим, что поиск музыкальных отношений в геометрических образах сильно увлекал античных исследователей. Не случайно из множества первоклассных открытий Архимед больше всего ценил открытие отношения объемов и площадей поверхностей цилиндра и вписанного в него шара, равного 3/2, т. е. квинте.
Но и в отжившем учении Платона об атомах четырех стихий есть своя внутренняя мудрость. Стремление свести сложные природные явления к простым неразложимым компонентам остается содержанием и современного естествознания. Сейчас известно чуть более ста атомов элементов, из которых состоят все встречающиеся в природе вещества. Сверхзадачей современной физики является выявление "кирпичиков мироздания" - элементарных частиц - первичных, неразложимых далее частиц, из которых состоит вся материя. Еще в начале XX века считалось, что таких частиц три: электрон, протон и нейтрон. Однако катастрофический рост числа открываемых элементарных частиц привел во второй половине XX века к пересмотру воззрений об их элементарности. Сегодня есть основания считать, что такие "экс-элементарные" частицы, как протоны, нейтроны, мезоны, гипероны и др., состоят из различных комбинаций трех типов кварков* (либо пар кварк - антикварк) - новых "кирпичиков мироздания". Не вдаваясь в дебри современной ядерной физики, отметим только, что, как и во времена Платона, принцип простоты является той нитью Ариадны, которая ведет сегодня физиков по темным лабиринтам микромира.
* (Любопытна история возникновения термина. Это название заимствовано американским физиком М. Гелл-Маном, высказавшим в 1964 г. гипотезу о существовании трех неизвестных частиц, из романа современного английского писателя Дж. Джойса "Поминки по Финегану". Хотя по-немецки "кварк" - это "творог", в романе слово означает нечто таинственное и непонятное. Герою романа снится сон, где чайки кричат: "Три кварка для мастера Марка". Так слово, изобретенное писателем Джойсом, стало едва ли не важнейшим термином современной ядерной физики. Вот они, узы науки и искусства!)

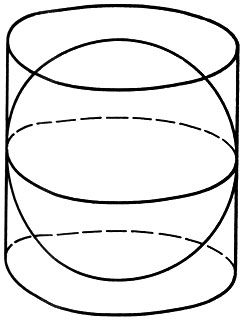
Теорему об отношении объемов и площадей поверхности цилиндра и вписанного в него шара Архимид считал своим высшим достижением. По завещанию Архимеда чертеж этих фигур был выполнен на его могильном камне
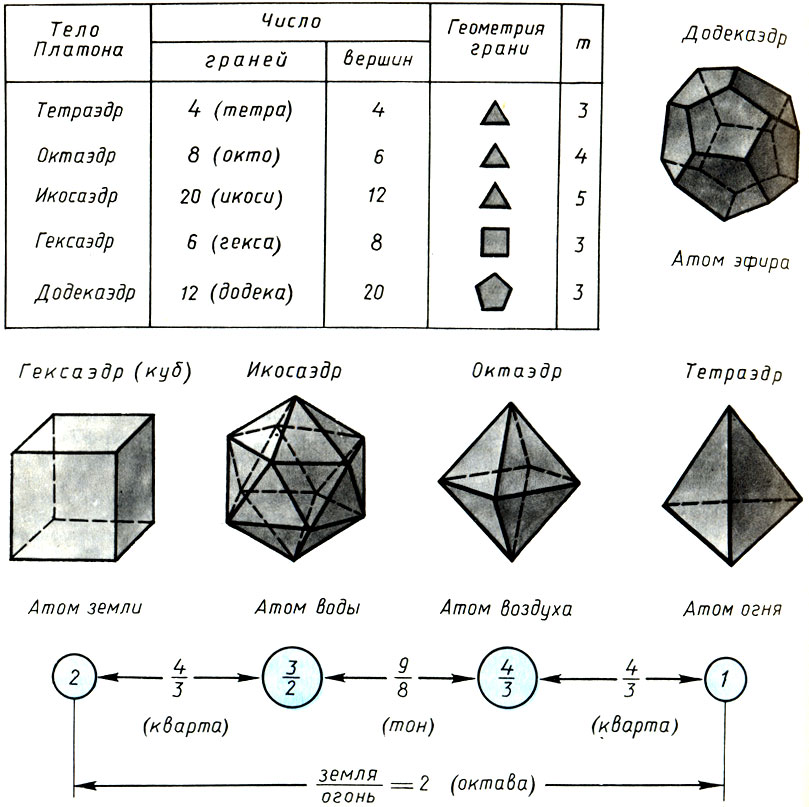
Непреходящие математические свойства правильных многогранников (таблица) и их наивная физическая интерпретация по Платону
Еще более современным выглядит стремление Платона видеть элементы материи в виде правильных симметричных тел. Современная наука все глубже проникает в тайну того, что внешние проявления симметрии - от симметрии кристаллов и снежинок до симметрии молекул ДНК - есть следствие симметрии тех фундаментальных законов, которые управляют всеми процессами физического мира. Таким образом, то, что на заре цивилизации античные философы видели атомы в виде симметричных геометрических тел" должно вызывать не саркастическую усмешку, а, скорее, удивление.
Учения о четырех стихиях и гармонии сфер из античности перешли в средневековье. Народное творчество, фантазия средневековых алхимиков и воображение поэтов населили четыре Платоновы стихии мифическими существами - духами. Так появились подземные человечки - гномы или кобольды - духи земли; златокудрые русалки - ундины - с рыбьим хвостом вместо ног - духи воды; прекрасные существа, населяющие атмосферу, ростом не более дюйма с шапочкой из цветка на голове - сильфы или эльфы - духи воздуха; наконец, духи огня - саламандры, пляшущие в огне в виде ящериц. Страшные карлики-гномы охраняют подземные богатства, они сказочно богаты, любят дразнить людей, но чаще помогают им. Красавицы-ундины вечерами расчесывают на берегу свои пышные волосы. Однако они опасны, так как могут очаровать своей красотой и пением пылкого юношу и увлечь его в подводное царство. Танцы и музыка - любимое занятие эльфов, а если музыкант начнет играть мелодию эльфов, то он не сможет остановиться, пока не доиграет ее до конца. Знакомые с детства сказки Андерсена "Дюймовочка" и "Русалочка", сказка братьев Гримм "Белоснежка и семь гномов", комедия Шекспира "Сон в летнюю ночь", баллада Гёте "Лесной царь", поэма Жуковского "Ундина" и многие стихотворения многих авторов навеяны этими легендами. Так отжившая научная теория превращалась в красивую сказку.
Саламандра, жгись, Ундина, вейся, Сильф, рассейся, Кобольд, трудись! Кто слышит впервые Про эти стихии, Их свойства и строй, Какой заклинатель? Кропатель пустой!
Не менее популярным оставалось в средние века и учение о гармонии сфер. Вообще, считалось, что законы мироздания в основе своей являются музыкальными законами. Мысль эта прочно вошла в сознание не только средневековых ученых-схоластов, но и поэтов. Гармония сфер звучит в "Божественной комедии" великого Данте, написанной в начале XIV века:
Когда круги, которых вечный ход Стремишь, желанный, ты, мой дух призвали Гармонией, чей строй тобой живет, Я видел - солнцем озарились дали Так мощно, что ни ливень, ни поток Таких озер вовек не расстилали.
Несмотря на увлечение Данте числовой мистикой, архитектура его бессмертной поэмы является непревзойденным образцом математической строгости. Поэма делится на три части: "Ад", "Чистилище" и "Рай". В каждой части - 33 песни, что вместе со вступительной песнью дает 100 песен - квадрат "священного" числа 10 (см. с. 94). В каждой части и каждой песне практически одинаковое число стихов (строк), а каждая часть заканчивается одним и тем же словом - stella (звезда, светило). Описываемое Данте мироздание построено на числе 9 - квадрате символа определенности числа 3: в Аду - 9 кругов, в Раю - 9 небес, семь кругов Чистилища и два уступа предчистилища также дают число девять и т. д.
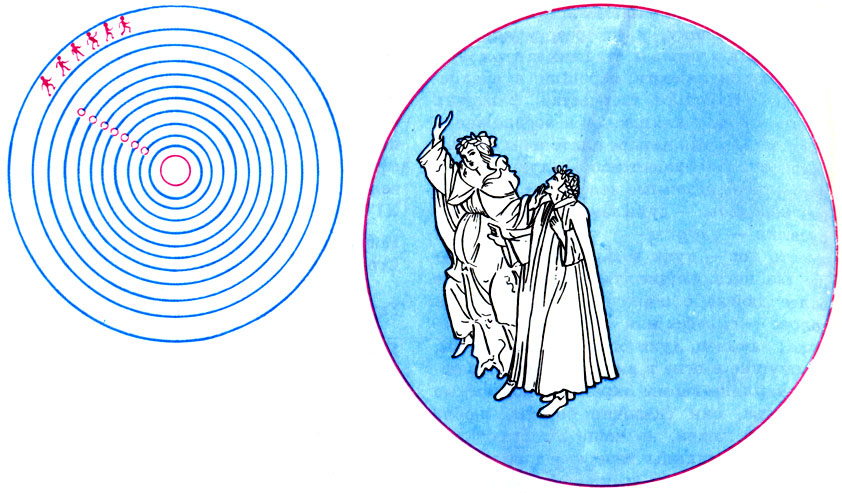
Боттичелли. Иллюстрация к 'Божественной комедии' Данте. 1492-1497. Данте, влекомый Беатриче, взирает на геоцентрическую систему мироздания
Заключительные аккорды "космической музыки" прозвучали в работах Иоганна Кеплера (1571 -1630) - выдающегося немецкого математика, физика, астронома. Следуя пифагорейско-платоновской традиции, Кеплер верил, что в основе мироздания лежат простые числовые соотношения и совершенные геометрические формы. Но Кеплер поставил и вопросы, достойные отца современного естествознания: почему планет (известных в то время) только шесть? Почему их орбиты имеют те, а не иные параметры?
Сначала молодой учитель математики Иоганн Кеплер тщетно ищет между параметрами планетных орбит простые числовые отношения. Но вдруг... Решая с учениками какую-то геометрическую задачу, он начертил на классной доске равносторонний треугольник со вписанной и описанной окружностями. Внезапно его
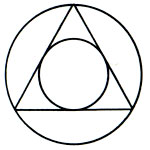
'Космическая музыка': от Платона до Кеплера
озарила мысль, что планетные орбиты связаны между собой посредством геометрических фигур. Однако расчеты показали, что плоские геометрические фигуры не удовлетворяли этой идее. Новые разочарования... "И вот я снова устремился вперед. Зачем рассматривать фигуры
двух измерений для пригонки орбит в пространстве? Следует рассмотреть формы трех измерений...",- вспоминал впоследствии Кеплер. Новые поиски и новое озарение: существует только шесть планет и, следовательно, пять промежутков между ними. Но и Платоновых тел только пять! Как трудно было допустить, что это простое совпадение!.. "Я еще не имел ясной идеи о порядке, в котором следует расположить правильные тела... День и ночь я проводил за расчетами... Через несколько дней все стало на свои места." Какой накал страстей в этих записях Кеплера!
Вскоре двадцатичетырехлетний учитель издает маленькую книжку с вычур ным названием, как требовала мода того времени,- "Предвестник космографических исследований, содержащий тайну мироздания относительно чудесных пр°" порций между небесными кругами и истинных причин числа и размеров небесных сфер, а также периодических движений, изложенный с помощью пяти правильных тел Иоганном Кеплером из Вюртемберга, математиком достославной провинции Штирии", или "Mysterium Сosniographicum" ("Тайна мироздания"), как любил называть ее сам Кеплер. Книга эта содержала формулу открытия Кеплера: в сферу орбиты Сатурна Кеплер вписывает куб, в куб - сферу Юпитера, в сферу Юпитера - тетраэдр, и так далее последовательно вписываются друг в друга сферы Марса - додекаэдр, сфера Земля - икосаэдр, сфера Венеры - октаэдр и сфера Меркурия. В центре всей системы коперниканец Кеплер помещает Солнце*. Тайна мироздания кажется раскрытой! Вселенная устроена на основе единого геометрического принципа!
* (Для каждого правильного многогранника существует вписанная сфера, касающаяся центров каждой грани, и описанная сфера, проходящая через все вершины, причем центры этих сФер совпадают. Таким образом, все построенные Кеплером сферы имеют общий центр.)
Что же показали математические расчеты? Конечно, совпадение с данными Коперника по радиусам планетных орбит было поразительным, но все-таки не столь точным, как того хотелось бы педантичному Кеплеру**.Особенно много хлопот доставила Кеплеру сфера Меркурия, которую в конце концов пришлось вписать в октаэдр так, чтобы -она касалась не граней, а середины ребер последнего. Остальные незначительные расхождения между теорией и опытными данными Кеплер объяснил тем, что реальные планетные сферы имеют некоторую толщину, что и позволило "выбрать" эти расхождения.
** (Заинтересовавшийся читатель может легко воспроизвести эти расчеты. Например, для куба с ребром а имеем R = a√3/2, r = a/2, откуда R/r = √3 1,732. Современные усредненные pадиусы орбит Сатурна и Юпитера соответственно равны Rс = 1,427*109 км и Rю = 0,788*109 км, откуда Rс/Rю= 1,834. По Коgерyику, Rс/Rю= 1,758.)
1,732. Современные усредненные pадиусы орбит Сатурна и Юпитера соответственно равны Rс = 1,427*109 км и Rю = 0,788*109 км, откуда Rс/Rю= 1,834. По Коgерyику, Rс/Rю= 1,758.)
Однако червь сомнения поселился в Душе Кеплера. Можно сказать, что оставшиеся тридцать лет жизни Кеплер посвятил "спасению" своей теории от самого себя. Эта работа привела к открытию истинных астрономических законов - трех знаменитых законов Кеплера, на базе которых Ньютон построил свою теорию тяготения. Сам же Кеплер в полной мере не осознал своих настоящих открытий и до конца жизни более всего любил свою первую работу.
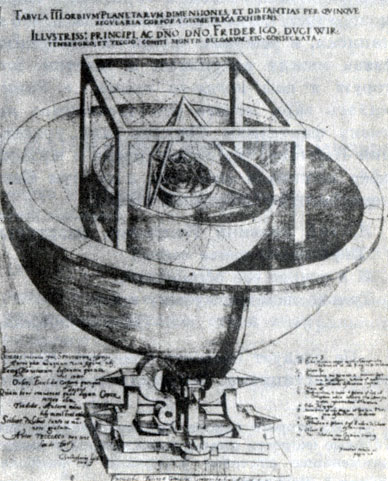
Космический кубок Кеплера, Иллюстрация Иоганна Кеплера из его книги 'Тайна мироздания'. Тюбинген. 1596
Не забыл Кеплер и о самой "музыке" сфер. Поискам гармонических соотношений посвящена одна из глав книги "Гармония мира" (1619), которую он считал своей вершиной: "жребий брошен. Я написал книгу либо для современников, либо для потомков..." Кеплер установил семь основных гармонических интервалов (консонансов): октаву (2/1), большую сексту (5/3), малую сексту (8/5), чистую квинту (3/2), чистую кварту (4/3), большую терцию (5/4) и малую терцию (6/5), из которых он выводит весь звукоряд как мажорного, так и минорного наклонения. После долгих поисков гармонических соотношений "на небе", проделав огромную вычислительную работу, Кеплер наконец установил, что отношения экстремальных (наибольших и наименьших) угловых скоростей* для некоторых планет близки к гармоническим: Марс - 3/2, Юпитер - 6/5, Сатурн - 5/4. "Солнце гармонии засияло во всем блеске... Небесные движения есть не что иное, как ни на миг не прекращающаяся многоголосая музыка". И здесь Кеплера не оставляет буйная фантазия. Небольшие расхождения теории и эксперимента он объясняет тем, что небесный секстет должен звучать одинаково согласованно и в миноре, и в мажоре, а для этого ему необходимо иметь возможность перестраивать свои инструменты. Далее Кеплер утверждает, что Сатурн и Юпитер "поют" басом, Марс - тенором, Земля и Венера - альтом, а Меркурий - дискантом. Никаких математических "доказательств" здесь он не приводит. Да и сам Кеплер устал в поисках всеобщей гармонии: "Мой мозг устает, когда я пытаюсь понять, что я написал, и мне уже трудно восстановить связь между рисунками и текстом, которую я сам когда-то нашел..." Занималась заря нового естествознания: на смену фантазиям Кеплера шли уравнения Ньютона. Красивая сказка о музыке сфер доживала свой век, и работы Кеплера были ее лебединой песней.
Я, как древний Коперник, разрушил Пифагорово пенье светил И в основе его обнаружил Только лепет и музыку крыл.
* (Из второго закона Кеплера следует, что угловые скорости планет непостоянны и имеют наименьшее значение в афелии и наибольшее - в перигелии.)
Не следует спешить обвинять Кеплера в мистицизме, богоискательстве, числовых спекуляциях и увлечении отжившими античными теориями. Правильнее видимо, вспомнить о времени, в которое он жил и творил: XVI век закончился костром на площади Цветов в Риме, где 17 февраля 1600 Г. был сожжен Джордано Бруно. Следует вспомнить трагическую историю матери Кеплера, Катерины Кеплер, которую публично объявил ведьмой и процесс над которой тянулся долгие 6 лет. Обвиняемую заковывали в цепи, ставили перед палачом с орудиями пыток, и только искусные действия ее сына Иоганна, который сам вел защиту, позволили выиграть процесс у церковных мракобесов. "Арестованную, к сожалению, защищает ее сын, господин Иоганн Кеплер, математик",- свидетельствовал судебный писец. Только в родном городе Кеплера Вейле с 1615 по 1629 г. ужасная смерть постигла 38 "колдуний". Вот в какое время рождалось современное естествознание!
"Мы имели дело с человеком тонких чувств, всецело и страстно увлеченным поиском пути к более глубокому проникновению в сущность явлений природы, с человеком, который, несмотря на внутренние и внешние трудности, сумел достичь поставленной перед собой возвышенной цели" - так характеризовал личность Кеплера Альберт Эйнштейн, Кеплер XX века, по справедливому определению физиков наших дней.
Заканчивая наше необычное "музыкальное обозрение", перенесемся в 20-е гг. XX века, когда вновь неожиданно зазвучало "пифагорово пенье светил". Согласно теории Нильса Бора, развитой им в 1913 г., движение электрона вокруг атомного ядра возможно только по избранным "разрешенным" орбитам, двигаясь по которым электрон вопреки законам классической электродинамики не излучает энергии, но может скачком переходить с одной орбиты с энергией Ei на другую "дозволенную" орбиту с энергией Еk, испуская (i>k) или поглощая (i<k) при этом порцию ("квант") электромагнитной энергии с частотой
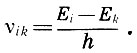 (7.2)
(7.2)h - постоянная Планка.
В простейшем случае атома водорода, содержащего один электрон, энергия n-го энергетического уровня равна
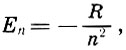 (7.3)
(7.3)R - постоянная Ридберга.
Здесь n = 1, 2, 3,... называется главным квантовым числом. Тогда совокупность частот, излучаемых атомом водорода при переходе с верхнего энергетического уровня на нижний (i>k), определяет спектр испускания данного атома и каждому такому переходу соответствует своя спектральная линия. Для атома водорода согласно формулам 7.2, 7.3 получаем совокупность спектральных линий с частотами
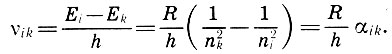
При переходе со второго, третьего и т. д. энергетических уровней ni = 2, 3, 4... на первый nk = 1 получается так называемая "спектральная серия Лаймана", для которой α21=3/4, α31=8/9, α41 = 15/16. Но ведь это кварта (3/4), тон (8/9) и полутон в чистом строе (15/16)! "Таким образом,- писал А. Эйнштейн,- мы открыли некоторое подобие между колебанием струны и атомом, испускающим излучение".
"То, что нам сегодня удается понять на языке спектров,- это истинная музыка атомных сфер, созвучие целочисленных отношений, все возрастающие порядок и гармония при всем их многообразии - так восторженно отзывался о квантовой теории немецкий физик и математик Арнольд Зоммерфельд (1868-1951).- ... Она представляет собой тот полный таинства инструмент, на котором природа исполняет спектральную музыку и ритмом которого она управляет строением атома и атомных ядер".
Итак, обыкновенная музыкальная гамма увлекла нас вслед за Пифагором, Платоном и Кеплером в путешествие по просторам космоса. Мы узнали, что "пифагорово пенье" услышали и физики XX века, но уже не в космосе, а в противоположной стихии - микромире. Но нам пора от "физических приложений" вновь вернуться к математическому содержанию музыкальной гаммы, которая таит в себе еще немало секретов.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'