
5. Пифагор и пифагорейское учение о числе
Греки совершили открытие, величайшее из когда-либо совершенных человеком: они открыли могущество разума.
С берегов Средиземноморья - "колыбели европейской цивилизации", с тех давних времен, названных через много веков "весною человечества", дошло до нас имя Пифагора - математика, философа, мистика. Мы не знаем доподлинно портрета Пифагора, не сохранилось ни одной строки из его сочинений; его биография стала легендой, полной невероятных преувеличений, а самого Пифагора назвали "на одну десятую гением, на девять десятых выдумкой". По преданию, вид его был так величествен, что ученикам часто казалось, будто это сам бог Аполлон говорит с ними.
Пифагор - едва ли не самый популярный ученый не только в античности, но и в наши дни. И дело, конечно, не в том, что "таблица Пифагора" смотрит на нас с любой тетрадки в клеточку. Дело в том, что "то ли по счастливому стечению обстоятельств, то ли благодаря гениальной интуиции пифагорейцам удалось сформулировать два тезиса, общезначимость которых подтвердило все последующее развитие науки: во-первых, что основополагающие принципы, на которых зиждется мироздание, можно выразить на языке математики; во-вторых, что объединяющим началом всех вещей служат числовые отношения, которые выражают гармонию и порядок природы". Так определяет роль Пифагора в современной науке американский математик М. Клайн.
Что же известно о Пифагоре? Родился Пифагор на острове Самос, расположенном в Эгейском море у берегов Малой Азии, около 570 г. до н. э. Остров Самос известен пробитым под горою Кастро туннелем, по которому проходил водопровод, снабжавший город Самос питьевой водой. Туннель строился с двух сторон, причем расчеты, без которых в этом деле не обойтись, были настолько точными, что оба хода сошлись под горой с незначительной ошибкой. Самосский туннель, построенный около 530 г. до н. э., является едва ли не единственным замечательным подтверждением математической подготовки греческих строителей - современников Пифагора, свидетельствует о высоком уровне математики того времени и смелом ее применении.
Отец Пифагора Мнесарх был резчиком по драгоценным камням. Будучи пытливым юношей, Пифагор отправился в путешествие по странам Востока, спускался в знаменитую пещеру Крита, с которой греки связывали миф о сотворении богов, был в Египте, где якобы попал в плен к персам и был увезен в Вавилон. Это несчастье сыграло счастливую роль в судьбе Пифагора: вавилонская наука, и в частности математика, была передовой наукой того времени, и у халдейских мудрецов было чему поучиться. И хотя о странствиях Пифагора, как и о всей его жизни, нет достоверных данных, взаимосвязь вавилонской математики и математики Пифагора (вспомним хотя бы, что знаменитая теорема Пифагора была известна без доказательства вавилонянам) указы-" вает на то, что Пифагор во многом воспринял восточную мудрость. Египетские жрецы и вавилонские халдеи привили также Пифагору пристрастие к восточным таинствам, магии и числовой мистике.

Предполагаемый бюст Пифагора. Найден при раскопках Геркуланума близ Помпеи. Бронзовая копия с греческого оригинала. IV в. до н. э. (?)
Вернувшись на родину, Пифагор собирает вокруг себя единомышленников, приспособив для занятий философией одну из пещер, где проводит почти все дни и ночи. Однако вскоре он покидает родной город в знак протеста против деятельности правителя Самоса, тирана Поликрата, считая, что свободный человек не должен подчиняться произволу и деспотизму. Согласно преданию, на сороковом году жизни Пифагор поселился в южноиталийском городе Кротоне. Здесь он "сразу привлек всеобщее уважение как человек, много странствующий, многоопытный и дивно одаренный судьбою и природою: с виду он был величав и благороден, а красота и обаяние были у него и в голосе, и в обхождении, и во всем",- писал в "Жизни Пифагора" древнегреческий философ Порфирий (233-304) В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена, члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Система жизненных принципов и правил, проповедуемая Пифагором, и сейчас достойна подражания. Так, Пифагор учил: "беги от всякой хитрости, любым орудием отсекай от тела болезнь, от души - невежество, от утробы - роскошество, от семьи - ссору, от всего, что есть - неумеренность". День пифагорейцу надлежало заканчивать вопросом:
"Не допускай ленивого сна на усталые очи, Прежде чем на три вопроса о деле дневном не ответишь: Что я сделал? чего не сделал? и что мне осталось сделать?"
и начинать с вопроса:
"Прежде чем встать от сладостных снов, навеваемых ночью, Думой раскинь, какие дела тебе день приготовил".
Сам Пифагор начинал занятия ранним утром, успокоив душу игрою на лире и пением стихов Гомера, предпочитал уединенные прогулки, замечая при этом, что "где тише всего, там и краше всего". Система этических правил Пифагора была собрана в своеобразный моральный кодекс пифагорейцев - "Золотые стихи".
Пифагор предписывал чтить старейших, "ибо всюду предшествующее почетнее последующего". Пифагор высоко ценил дружбу, считая, что у друзей все общее и что друг - это второе я. Скромность и пристойность он видел в том, чтобы не хохотать и не хмуриться, избегать издевок и пошлых рассказов. В еде он довольствовался хлебом, медом и овощами и воздерживался от животной пищи*. Носил Пифагор ослепительно белые одежды. К сожалению, реальные и вызывающе глубокое уважение к личности Пифагора сведения были перемешаны со множеством сказок и легенд, которые со врежем породили несерьезное отношение Пифагору как исторической личности. Легенды наперебой объявляли Пифагора чудотворцем: сообщали, что у него было золотое бедро; что люди видели его одновременно в двух разных местах говорящим со своими учениками; что однажды, когда он с многочисленными спутниками переходил реку и заговорил с ней, река вышла из берегов и воскликнула: "Да здравствует Пифагор!"; что он предсказывал землетрясения, останавливал повальные болезни, отвращал ураганы, укрощал морские волны и т. д.
* (Порфирий приводит любопытный эпизод. Проведуя вегетарианство, Пифагор тем не менее посоветовал самосскому атлету Евримену ежедневно питаться мясом, а не сыром и смоковами, как это делали остальные спортсмены. Евримен последовал Пифагоровой мудрости - набрался сил и, несмотря на свой малый рост, одержал победу в борьбе на Олимписких играх. )
Ритуал посвящения в члены пифагорейского братства был окружен множеством таинств, разглашение которых сурово каралось. Но и попав в орден после строгого отбора и испытательного периода, новички могли только из-за занавеса слушать голос Учителя, видеть же его самого разрешалось только после нескольких лет аскетической жизни. "Стремление уйти от мира, замкнутая монашеская жизнь, вегетарианство и общность имущества встречались у многих сект. Но что отличало пифагорейцев от всех других - это способ, при помощи которого они считали возможным достигнуть очищения души и соединения с божеством; это делалось именно при помощи математики. Математика была одной из составных частей их религии". Эта меткая характеристика пифагорейского братства принадлежит известному голландскому математику и историку науки Б. Л. ван дер Вардену.
Итак, именно в математике, в познании количественных отношений, видели пифагорейцы ключ к разгадке мировой гармонии, постижение которой и составляло-смысл их жизни. Но почему постижение всеобщей гармонии ставилось высшей жизненной целью? Дело в том, что пифагорейцы верили в бессмертие души и переселение души человека в животных**. Поэтому они полагали, что посвящение в тайны всеобщей гармонии, т. е. стремление к истине, приближает душу человека к божеству, создавшему эту гармонию, вследствие чего душа сможет освободиться от дальнейших перевоплощений.
** (Известна легенда, рассказывающая, что однажды, увидев, как били собаку, Пифагор сказал: "Перестаньте ее бить, в этой собаке живет душа моего друга: я узнал его по голосу".)
Учение Пифагора носило эзотерический, т. е. тайный, характер и не излагалось письменно, почему и не сохранилось никаких письменных трудов самого Пифагора. В силу этого, а также в силу существовавшей в античности традиции приписывать результаты открытий учеников своему учителю практически невозможно определить, что сделал в науке сам Пифагор, а что - его ученики и представители пифагорейской школы. Споры вокруг "пифагорейского вопроса" ведутся третье тысячелетие, однако общего мнения не существует и поныне. Вот почему принято осторожно говорить "пифагорейское учение", а не "учение Пифагора".
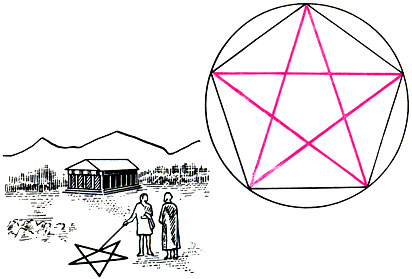
Звездчатый пятиугольник, или пентаграмма,- пифагорейский символ здравия и тайный опознавательный знак
Обет молчания, даваемый пифагорейцами, нашел отражение в символе "бык на языке", что на современный лад означает "держи язык за зубами". Вообще, пифагорейцы имели множество знаков и символов, которые были своего
рода заповедями, например: "через весы не шагай", т. е. не нарушай справедливости; "огня ножом не вороши", т. е. не задевай гневных людей обидными словами; "не ешь сердца", т. е. не подтачивай душу страстями или горем.
Но главным пифагорейским символом - символом здоровья и опознавательным знаком - была пентаграмма или пифагорейская звезда - звездчатый пятиугольник, образованный диагоналями правильного пятиугольника. Звездчатый пятиугольник обладает замечательными математическими свойствами, которые мы рассмотрим в главе 15. Он содержит все пропорции, известные пифагорейцам: арифметическую, геометрическую, гармоническую и так называемую золотую. Видимо, поэтому пентаграмма и была выбрана в качестве пифагорейского символа.
Нарисованная пентаграмма была тайным знаком, по которому пифагорейцы узнавали друг друга. Согласно легенде, когда один пифагореец умирал на чужбине и не мог расплатиться с гостеприимным хозяином дома, ухаживавшим за ним, он велел хозяину нарисовать на стене своего дома пентаграмму. "Если когда-нибудь мимо пройдет пифагореец, он обязательно сюда заглянет",- сказал умиравший. Действительно, через несколько лет другой странствующий пифа гореец увидел знак, расспросил о случившемся хозяина и щедро вознагради его.
Однако в первоначальном виде пифагорейский союз просуществовал недолго и к концу VI века (ок. 510 г. до н. э.) подвергся кровавой расправе. Пифагорейцы бежали из Кротона в другие города, что во многом способствовало распространению учения Пифагора по всей Греции и даже за ее пределы. Сам Пифагор удалился в город Метапонт, расположенный неподалеку от Кротона, где и провел остаток своей жизни.
Смерть Пифагора также окружена красивыми легендами. По одной из них, дом в Кротоне, где Пифагор собирался со своими учениками, был подожжен. Преданные друзья бросились в огонь и проложили в нем дорогу учителю, чтобы он по их телам вышел из огня, как по мосту. Друзья погибли, а сам Пифагор, будучи спасенным столь дорогой ценой, так затосковал, что лишил себя жизни. Умер Пифагор около 500 г. до н. э.
Подлинно новым и революционным в пифагорейской научной системе явилось учение о числе, которое мы рассмотрим в трех аспектах: философском, математическом и музыкальном. В числовых отношениях, т. е. в математике, видели пифагорейцы сущность мировой гармонии, ключ к разгадке всех тайн природы, окруженных ореолом мифологии. Вообще, развитие пифагореизма шло от мифологии через философию к науке. Пифагорейская наука была еще слишком близка к мифологии, чем и объясняется царившее в ней "мифологическое начало". Но то, что в математических свойствах пифагорейцы увидели сущность явлений природы, то, что в основе разнородных процессов они обнаружили некоторую пропорциональность, закономерность, выражаемую числом, было выдающимся научным завоеванием. "Подобно тому как число подчинено определенным законам, подчинена им и вселенная; этим впервые высказывается мысль о закономерен вселенной",- так характеризовал роль пифагорейского учения о числе Ф. Энгельс (т. 20, с. 503).
Примечательно, что отправным пунктом в пифагорейском учении о числе была музыка. Именно в музыке была первые обнаружена таинственная направляющая роль чисел в природе. По преданию, сам Пифагор установил, что приятные слуху созвучия получаются лишь в том случае, когда длины струн, издающих эти звуки, относятся как целые числа первой четверки: 1:2, 2:3, 3:4 (см. гл. 6). Это открытие потрясло Пифагора и долго вдохновляло его учеников на поиски новых числовых закономерностей в природе. По мнению выдающегося немецкого физика А. Зоммерфельда, день, когда было сделано это открытие, можно назвать днем рождения математической физики.
Вот как описывает этот день римский философ и сенатор Северин Боэций (480- 524): "И вот однажды, под влиянием какого-то божественного наития, проходя мимо кузниц, он слышит, что удары молотков из различных звуков образуют некое единое звучание. Тогда, пораженный, он подошел вплотную к тому, что долгое время искал, и после долгого размышления решил, что различие звуков обусловлено силами ударяющих, а для того чтобы уяснить это лучше, велел кузнецам поменяться молотками. Однако выяснилось, что свойство звуков не заключено в мышцах людей и продолжает сопровождать молотки, поменявшиеся мерами. Когда, следовательно, Пифагор это заметил, то исследовал вес молотков. Тих молотков было пять, причем обнаружилось, что один из них был вдвое больше Другого и эти два отвечали друг другу соответственно созвучию октавы. Вес вдвое большего был на 4/3 больше веса третьего, а именно того, с которым он звучал в кварту...
Вернувшись домой, Пифагор путем различного исследования стал выяснять, заключается ли в этих пропорциях вся причина созвучия (Трактат о музыке)".

Пифагор со своими учениками. Иллюстрация из книги Франкино Гафурио 'Теория музыки'. Милан. 1492. Гравюры изображают акустические опыты Пифагора и Филолая на сосудах, струнах и трубках, находящихся в отношениях 4:6: :8:9:12:16
Только что появившаяся на свет пифагорейская наука еще не могла отделить абстрактное понятие числа от конкретного материального объекта. Видя в числах сущность явлений, начало начал, пифагорейцы считали, что реальные тела состоят из "единиц бытия" - "математических атомов", различные комбинации которых и представляют конкретные объекты. Даже вселенная мыслилась ими как совокупность чисел. Сами же числа пифагорейцы представляли наглядно и материально: единица трактовалась как абсолютная и неделимая единичность, т. е. точка, "геометрический атом" или первооснова всех чисел; два - как уход в неопределенную даль, т. е. прямая линия, простирающаяся в одном измерении; три - треугольник, образующий плоскость двух измерений, и возврат к определенности; четыре - пирамида, дающая представление о пространстве трех измерений. Вообще, числа 1, 2, 3, 4 играли у пифагорейцев особую роль и образовывали тетрактис, или четверку. По преданию, клятва пифагорейцев гласила: "Клянусь именем Тетрактис, ниспосланной нашим душам. В ней источник и корни вечно цветущей природы". Особая роль тетрактиса, видимо, была навеяна законами музыкальных созвучий, после чего все объекты природы виделись пифагорейцам состоящими из четверок: четверка геометрических элементов - точка, линия, поверхность, тело; четверка физических элементов - земля, вода, огонь, воздух. (Учение Платона о четырех физических элементах, четырех стихиях, мы рассмотрим в главе 7.) Сумма же чисел, образующих тетрактис, равная десяти (10 = 1 + 2+ 3 + 4), считалась священным числом и олицетворяла всю вселенную.
Так родился знаменитый пифагорейский тезис: "Все вещи суть числа". Этот тезис, если забыть о его внутреннем содержании, а тем более если числа отождествлять с цифрами, многим представлялся попросту абсурдным. Далее, считая, что материальный мир состоит из чисел, т. е. из идей, пифагорейцы, сами того не сознавая, становились на позиции философского идеализма, и не случайно именно на почве пифагореизма возникло учение основоположника объективного идеализма в философии Платона. Наконец, интерес к числу часто носил у пифагорейцев религиозно-мистический характер*. Но всякое явление следует рассматривать в его историческом окружении "Идеалистическая мистификация чисел у пифагорейцев была следствием неразвитости науки и философии и строя мышления, близкого к мифологическому,- пишет современный болгарский философ Е. Данков.- Но за этой формой нельзя не видеть рационального содержания значение которого все яснее проступает на современном уровне развития научного познания".
* (Некоторые отголоски пифагорейской числовой мистики мы встречаем и в наши дни: например, обычай дарить нечетное число цветов (четное число у пифагорейцев считалось несчастливым).)
Наиболее страстно и убежденно роль числа в познании мира определил знаменитый пифагореец V века до н. э. Филолай. В одном из сохранившихся фрагментов сочинения Филолая "О природе" говорится: "В число же никогда не проникает ложь, потому что она противна и ненавистна его природе, истина же родственна числу и неразрывно связана с ним с самого начала".
Заканчивая разговор о философских аспектах пифагорейского учения о числе, хочется вспомнить и слова великого Гёте. Будучи не только гениальным поэтом, но и выдающимся мыслителем и разносторонним ученым; Гёте стряхнул с пифагорейской мудрости идеалистическую пыль: "Числа не управляют миром, но показывают, как управляется мир".
Перейдем теперь к математической стороне пифагорейского учения о числе. Числа пифагорейцы изображали в виде точек (возможно, камешками, расположенными на песке), которые они группировали в геометрические фигуры. Так возникли числа, сегодня именуемые фигурными:
линейные числа (в современной терминологии это простые числа), т. е. числа, которые делятся на единицу и на самих себя и, следовательно, представимы только в виде последовательности точек, выстроенных в линию  (линейное число 5);
(линейное число 5);
плоские числа - числа, представимые в виде произведения двух сомножителей 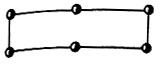 (плоское число 6);
(плоское число 6);
телесные числа, выражаемые произведением трех сомножителей 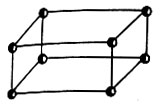 (телесное число 8);
(телесное число 8);
треугольные числа 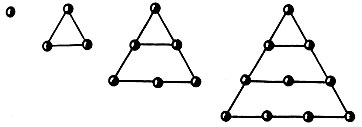 (треугольные числа 1, 3, 6, 10);
(треугольные числа 1, 3, 6, 10);
квадратные числа 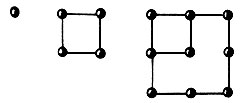 (квадратные числа 1, 4, 9);
(квадратные числа 1, 4, 9);
пятиугольные числа 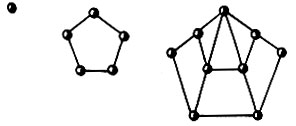 (пятиугольные числа 1, 5, 12)
(пятиугольные числа 1, 5, 12)
и т. д. Именно от фигурных чисел пошло выражение "возвести число в квадрат или куб".
Такое фигурное представление чисел часто помогало найти различные числовые закономерности. Например, написав последовательность квадратных чисел, легко увидеть (именно увидеть глазами!)
доказательство следующего математического утверждения:
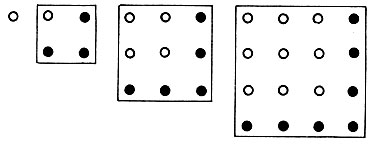
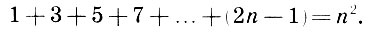
Аналогичное рассмотрение n-го треугольного числа приводит к равенству
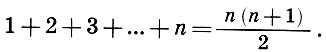
Фигура (обозначенная черными точками), которая, будучи приложенной к основной фигуре (белые точки), образует ей подобную, была названа Аристотелем гномоном. Первоначально слово "гномон" означало солнечные часы - прибор, позволяющий по линиям, которые пересекает тень от вертикального столбика, разделять беспредельность времени на очевидные части. Число для пифагорейцев и есть такой гносеологический гномон, дающий возможность различать вещи и тем самым овладевать ими в сознании. Живые организмы растут именно методом гномона, что позволяет сохранять присущую этим организмам форму.
Вообще, с изучения фигурных чисел, т. е. сумм некоторого числа единиц-точек (камешков), поставленных в виде определенной фигуры, началось изучение сумм числовых рядов. Это в свою очередь позволило Архимеду (ок. 287-212 гг. до н. э.) развить методы нахождения площадей и объемов фигур и тел и вплотную подойти к созданию интегрального исчисления, появившегося, однако, лишь 2000 лет спустя.
Рассмотрение чисел привело пифагорейцев к рассмотрению отношений между ними, т. е. пропорций. Пропорция с равными средними членами определяет среднее значение. По преданию, Пифагору были известны три вида средних значений, которые называли "древними":
арифметическое среднее 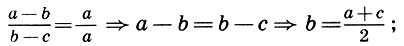
геометрическое среднее 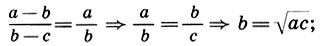
гармоническое среднее 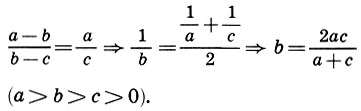
Обратим внимание на то, что среднее гармоническое величин а, b, с есть среднее арифметическое обратных величин 1/а, 1/b, 1/с. Пропорции и средние значения пифагорейцы наполняли не только математическим, но и философским и эстетическим содержанием, объясняя с их помощью и музыкальные созвучия, и даже всю вселенную.
Однако история науки, как и сама жизнь, полна неожиданных и драматических событий: среднее геометрическое таило в себе сокрушительный удар по всей пифагорейской системе; более того, нанести этот удар пифагорейцы, истинные рыцари науки, вынуждены были сами себе. Именно пифагорейцы обнаружили, что среднее геометрическое к числам 1 и 2 (в современных обозначениях 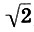 ) не выражается в виде отношения натуральных чисел, а других чисел древние греки не знали. Говоря языком геометрии, пифагорейцы установили, что диагональ квадрата, сторона которого равна 1, несоизмерима с этой стороной, т. е. отношение диагонали к стороне не выражается никаким целым или дробным числом. Выражаясь языком алгебры, пифагорейцы доказали, что уравнение m2=2n2 не имеет решений во множестве рациональных чисел*, что и потребовало введения чисел новой природы - иррациональных.
) не выражается в виде отношения натуральных чисел, а других чисел древние греки не знали. Говоря языком геометрии, пифагорейцы установили, что диагональ квадрата, сторона которого равна 1, несоизмерима с этой стороной, т. е. отношение диагонали к стороне не выражается никаким целым или дробным числом. Выражаясь языком алгебры, пифагорейцы доказали, что уравнение m2=2n2 не имеет решений во множестве рациональных чисел*, что и потребовало введения чисел новой природы - иррациональных.
* (Вот это доказательство. Допустим противное, т. е пусть 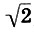 = m/n или m2 = 2n2, причем натуральные числа m и n не имеют oбщих делителей, кроме единицы, так как если бы они существовали, то на них дробь можно было бы сократить. Если m - нечетное число, мы получаем противоречие, так как 2n2 четно, а квадрат нечетного числа - число нечетное. Еcли m четно и равно 2k, то 4k2 = 2n2, или 2k2 = n2 так что n должно быть четным и, следовательно, числа m и n имеют общий делитель 2, что противоречит начальному предположению. Итак,
= m/n или m2 = 2n2, причем натуральные числа m и n не имеют oбщих делителей, кроме единицы, так как если бы они существовали, то на них дробь можно было бы сократить. Если m - нечетное число, мы получаем противоречие, так как 2n2 четно, а квадрат нечетного числа - число нечетное. Еcли m четно и равно 2k, то 4k2 = 2n2, или 2k2 = n2 так что n должно быть четным и, следовательно, числа m и n имеют общий делитель 2, что противоречит начальному предположению. Итак, 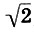 не является отношением двУх натуральных чисел)
не является отношением двУх натуральных чисел)
Иррациональность отношения стороны и диагонали квадрата пифагорейцы объясняли тем, что оба этих отрезка состоят из бесчисленного множества точек и поэтому отношение сводится к отношению двух бесконечно больших целых чисел. Хотя эта мысль не выдерживает критики для геометрических объектов, находящихся в рациональных отношениях (ведь они также состоят из бесчисленного множества точек!), по отношению к иррациональным числам она является справедливой. Действительно, всякое иррациональное число можно с любой степенью точности представить в виде отношения двух целых чисел, причем чем больше будут эти числа, тем точнее их отношение будет выражать иррациональное число.
Открытие несоизмеримости (для диагонали квадрата со стороной 1 не было соответствующего числа!) опрокидывало всю философскую систему пифагорейцев, которые были убеждены, что "элементы чисел являются элементами всех вещей и весь мир в целом является гармонией и числом". Это открытие долго держалось в тайне, а ученик Пифагора Гиппас из Метапонта за то, что он открыл недостойным участия в учениях природу пропорции и несоизмеримости, был изгнан из школы Пифагора. Позднее, когда Гиппас погиб во время кораблекрушения, его противники видели в этом наказание богов за разглашение тайны. Следует сказать, что пифагорейцы, не в пример иным ученым, после отчаянной борьбы против открытия, опрокидывавшего символ их "веры" признали свое поражение. Пытаясь выйти из тупика, они стали представлять величины не арифметически - числами, геометрически - отрезками. Так возникла геометрическая алгебра.
Между тем исторически именно это неосознанное открытие иррациональных чисел является наивысшим достижением пифагорейской школы; ему было суждено пережить тысячелетия и стать поворотным этапом в развитии математики, истоком современного математического анализа. С этого открытия начинается эра теоретической математики, ибо обнаружить несоизмеримые величины с помощью опыта невозможно.
Наконец, рассмотрим "музыкальную" сторону пифагорейского учения о числе. Как уже отмечалось, открытие математических закономерностей в музыкальных созвучиях послужило первым "экспериментальным" подтверждением пифагорейской философии числа. "Открытие Пифагора... было первым примером установления числовых связей в природе,- читаем мы в "Фейнмановских лекциях по физике".- Поистине должно быть было удивительно вдруг неожиданно обнаружить, что в природе есть факты, которые описываются простыми числовыми отношениями".
С этого времени музыка, точнее теория Музыки или учение о гармонии, занимает Почетное место в пифагорейской системе Знаний. "Музыкантов"-пифагорейцев интересует не столько музыкальное искусство, реальная музыка звуков, сколько е математические пропорции и соотношения, которые, как считалось, лежат в основе музыки. Многие греческие математики, в том числе Евклид (III в. до н. э.) и Клавдий Птолемей (85? -165?), посвятили музыкальным созвучиям и построению музыкальной шкалы специальные сочинения. Впрочем, поиски математических закономерностей в музыкальных созвучиях вели и через два тысячелетия такие великие математики, как Иоганн Кеплер, Готфрид Лейбниц, Леонард Эйлер.

Титульный лист книги Грегора Райха 'Маргарита философи-ка'. Фрайбург. 1503
Идея музыкальных соотношений настолько увлекла пифагорейцев, что они пытались обнаружить их всюду. В конце концов эта идея приняла "космические масштабы" и переросла в идею "всеобщей гармонии". Пифагорейцы утвердились в том, что вся Вселенная устроена на основе музыкальных, т. е. простых числовых, соотношений, что движущиеся планеты издают "музыку небесных сфер", а обычная музыка является лишь "отзвуком" царящей всюду "всеобщей гармонии" (см. гл. 7).
Таким образом, музыка и астрономия были сведены пифагорейцами к анализу числовых закономерностей, т. е. к арифметике и геометрии. Все четыре дисциплины стали считаться математическими и называться одним словом - "математа". Пифагорейское отношение к музыке как точной науке сохранилось и в средние века. Так, квадривиум (буквально - пересечение четырех дорог) - повышенный курс светского образования в средневековых университетах - состоял из четырех предметов: музыки, арифметики, геометрии и астрономии. "Высшая наука - математика - подразделяется на следующие искусства: арифметику, музыку, геометрию и астрономию - это определение римского писателя VI века Кассиодора (ок. 487- ок. 578).- Арифметика - учение о количестве, выражаемом числом, музыка же - учение, которое рассматривает числа по отношению к явлениям наблюдаемым в звуке". Вместе с тривииумом, содержавшим грамматику, риторику и диалектику, квадривиум составлял так называемые "семь свободных искусств" Это был, по мнению Кассиодора, своп элементарных знаний, необходимых монахам для понимания Библии, которму суждено было на протяжении целого тысячелетия представлять систему средневекового образования.
Как видим, термины "наука" и "искусство" в далекие времена античности практически не различались. Пифагорейцы называли математику и музыку родными сестрами. С тех пор дороги математики и музыки разошлись настолько, что их сопоставление сейчас многим покажется просто недоразумением. А ведь музыка пронизана математикой, как и математика полна поэзии и музыки! Это прекрасно чувствовали древние греки, и доказательство тому - содержание следующей главы.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'