
4. Симметрия, пропорция, гармония - слагаемые прекрасного
Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство.
Ничто не нравится, кроме красоты, в красоте - ничто, кроме форм, в формах - ничто, кроме пропорций, в пропорциях - ничто, кроме числа.
Гармония - магическое слово, сулящее всевозможные блага, это синтетическое понятие, слово завтрашнего дня.
"Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всем в жизни симметрия?" (Л. Толстой. "Отрочество").
Вместе с Николенькой Иртеньевым из трилогии Льва Толстого задумаемся и мы над тем, почему в природе царит симметрия. Почему симметрично все Живое от микроорганизмов до человека? Наконец, почему симметричное часто ассоциируется с прекрасным?

Бабочка парусник махаон - прекрасный пример билатеральной симметрии в природе
На первые два вопроса ответ существует: господство симметрии в природе прежде всего объясняется силой Тяготения, действующей во всей Вселенной. Действием Тяготения или отсутствием такового объясняется то, что и Космические тела, плывущие во Вселенной, и Микроорганизмы, взвешенные в воде, обладают высшей Формой симметрии - сферической (при любом повороте относительно центра фигура совпадает сама с собой). Все организмы, растущие в прикрепленном состоянии (деревья) или живущие на дне океана (морские звезды), т. е. организмы, для которых направление силы тяжести является решающим, имеют ось симметрии (множество всевозможных поворотов вокруг центра сужается д0 множества всех поворотов вокруг вертикальной оси). Наконец, для животных, способных передвигаться в воде, воздухе или по земле, кроме направления силы тяжести, важным оказывается и направление движения животного. Такие животные могут обладать только плоскостью симметрии, которая определяется векторами силы тяжести и направления движения. Биологи эту плоскость симметрии называют билатеральной, а тип симметрии - зеркальным. Ясно, что в случае асимметричного развития животного поворот в одну из сторон был бы для него затруднен и естественным для животного стало бы не прямолинейное, а круговое движение. Хождение же по кругу рано или поздно закончится трагически для животного. Билатеральной симметрией обладает, например, автомобиль, одинаково хорошо поворачивающий и вправо, и влево, чего нельзя сказать о мотоцикле с коляской, который такой симметрией не обладает и постепенно вытесняется автомобилем и своим двухколесным (зеркально-симметричным) собратом.
Любопытно, что переход от сферической симметрии у низших животных к зеркальной у высших (в частности, у человека) пытались объяснить еще древние греки. Так, в диалоге Платона "Пир" Аристофан рассказывает о том, что первоначально люди были круглыми, "спина не отличалась от груди, рук было четыре, ног столько же, сколько и рук, и у каждого на круглой шее два лица, совершенно одинаковых... Страшные своей силой и мощью, они питали великие замыслы и посягали даже на власть богов...
И вот Зевс и прочие боги стали совещаться, как поступить с ними... Наконец, Зевс, насилу кое-что придумав, говорит:
- Кажется, я нашел способ и сохранить людей, и положить конец их буйству, уменьшив их силу. Я разрежу каждого из них пополам, и тогда они, во-первых, станут слабее, а во-вторых, полезней для нас, потому что число их увеличится. И ходить они будут прямо, на двух ногах. А если они и после этого не угомонятся и начнут буйствовать, я, сказал он, рассеку их пополам снова, и они запрыгают у меня на одной ножке".
Симметрия господствует на Земле благодаря силе тяготения. Более того, поскольку эта сила действует повсюду во Вселенной, то и предполагаемые космические пришельцы не могут быть безудержно чудовищами, как их порой изображают, а обязательно должны быть симметричными.
Таким образом, мы подошли к самому трудному вопросу: "почему симметрия приятна для глаз?" Этот вопрос является составной частью более широкой проблемы: существуют ли объективные законы прекрасного? В чем тайна прекрасного, которая делает красоту предметом поклонения?

Симметрия, пропорция, гармония - слагаемые прекрасного
"Человек останавливается, пораженный, перед такими вещами, какие не могут играть никакой роли в его жизни: перед отражениями воды, которые нельзя схватить, перед отвесными скалами, которые нельзя засеять, перед удивительным цветом неба",- писал английский теоретик искусства Джон Рескин (1819-1900). Сколько усилий ума и сердца потрачено на постижение этой тайны! Вместе с истиной (наукой) красота (искусство) влекла за собой лучших представителей всех времен и народов. Но в отличие от истины красота понятна человеку даже тогда, когда ее внутренние закономерности остаются непознанными. Так, каждый достаточно ясно видит разницу между правильными и неправильными чертами человеческого лица, но до сих пор никто не может сформулировать точно закон, которому подчинена форма красивого лица, хотя такие попытки делались еще в глубокой древности. Или, скажем, струи наклонно бьющих фонтанов привлекают правильностью и красотою своих линий, хотя отнюдь не каждый знает, что это параболы, и тем более не в состоянии написать их уравнения. Пользуясь тем, что красота часто понятна интуитивно, без предварительной подготовки, люди искусства порой не хотят говорить о законах красоты, считая, что наука и искусство несовместимы. Суть этой неприязни искусства к науке заключена в убеждении, что математически точный закон обедняет искусство, лишает его некоей таинственности, вносит будни в праздник поэзии.
Разумеется, это не так. И лучшие представители искусства это ясно понимали. "Красота... следует своим собственным законам",- считал Шиллер. Гёте подчеркивал: "Для прекрасного требуется закон, который входит в явление". О людях науки говорить не приходится. "Если ты хочешь наслаждаться искусством, писал К. Маркс,- то ты должен быть художество образованным человеком"*.
* (Маркс К., Энгельс Ф. Из ранних произведений.- М., 1956.- с. 620. )
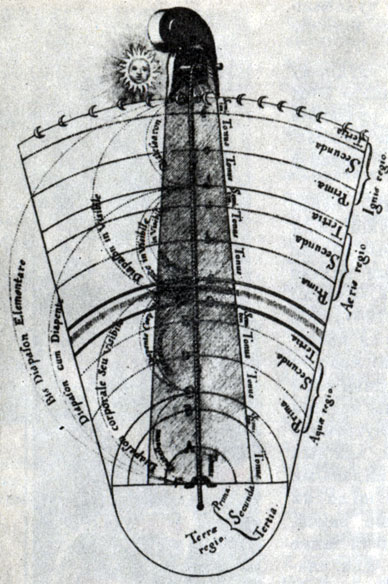
Монохорд, или Гармония мира. Иллюстрация к трактату Р. Флудда 'О космическом двуединстве'. Франкфурт. 1617. Со времен Пифагора музыка была для греков синонимом математической гармонии мироздания
Поиски объективных законов прекрасного велись с незапамятных времен, и первые находки здесь закономерно выпали на долю древних греков. Античная эстетика не только выработала систем взглядов, которые характеризуют эстетическое сознание древних греков, но и оказала решающее влияние на все последующее развитие эстетической культуры человечества.
Греки верили, что все мироздание по своей глубокой сущности прекрасно. Поэтому Вселенную они называли словом "космос", что значит "прекрасно устроенный". А коль скоро красота лежит в основе космоса, то искусству остается только открыть эти объективные законы красоты и руководствоваться ими.
Какие же объективные критерии прекрасного были выработаны в античную эпоху? Прежде всего, это категория меры, включающая в себя как составные элементы понятия симметрии, пропорциональности и ритма, и категория гармонии. Мера характеризует общие принципы строения, целостность предмета, тогда как понятия симметрии, пропорциональности и ритма добавляют к характеристике целого тот или иной специфической оттенок. Исходя из меры, определяет красоту Аристотель: "Красота заключается в величине и порядке, вследствие чего ни чрезмерно малое существо не могло бы стать прекрасным, так как обозрение его, сделанное в почти незаметное время, сливается, ни чрезмерно большое, так как обозрение его совершается не сразу, но единство и целостность его теряются для обозревающих.. ."
Принцип меры носил у древних греков не только формальный структурно-математический характер. Мера для греков - это прежде всего человек, это норма поведения, закон мироздания, структура художественного произведения. Греческое искусство возвеличивало человека даже тогда, когда говорило о богах.
Понятия симметрии, пропорции и ритма играли важную роль в познании греками пространственно-временной структуры окружающего мира. Закономерность и красота мироздания раскрывались перед ними и в симметрии живых организмов, и в пропорциональности человеческого тела, и в ритмах чередования дня и ночи, смены времен года и т. д. Вся античная архитектура и скульптура воплощали в себя эти принципы красоты. Блестящими примерами тому служат и величественные пропорции Парфенона, и знаменитый "Канон" Поликлета - скульптура и теоретический трактат, в которых автор попытался воплотить идеальные" по его мнению, пропорции мужского тела.

Поликлет. Дорифор (копьеносец), или Канон. Ок. 440 до н. э. Римская копия с утраченного оригинала. В пропорциях статуи воплощен закон золотого сечения
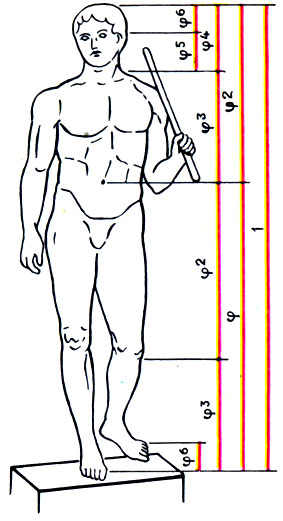
Приведен математический анализ пропорций Канона
Ведь назначение и цель гармонии - упорядочить части, вообще говоря, различные по природе, неким совершенным соотношением так, чтобы они одна другой соответствовали, создавая красоту.
Не менее содержательным было и античное понятие гармонии. В древнегреческой философии гармония в противоположность хаосу означала организованность Вселенной. Гармония трактовалась не как внешнее объединение разрозненных частей, а как внутреннее их единство, как единство противоположностей предела и беспредельного, частей и целого. Пифагор, не только великий математик, но и основоположник античной эстетики, считал, что гармония "внутренне присуща вещам, из которых составлен мир". Ее только нужно извлечь из вещей, что и делает художник благодаря своему мастерству, уму и таланту. В главе 7 мы познакомимся с пифагорейским учением о гармонии сфер, согласно которому расстояния между планетами соответствуют числовым отношениям музыкальной гаммы и весь космос звучит единым благозвучным аккордом. Вообще, пифагорейцы благоговели перед количественной картиной мира, выраженной в числе. Это была своеобразная философия числа, о которой мы расскажем в главе 5. Понятию гармонии древнегреческий философ Платон придал социальное значение, рассматривая гармонию как совокупность физических достоинств и высоких нравственных принципов человека-гражданина. Отсюда пошло выражение "гармонически развитая личность".
Разумеется, античная эстетика не решила всех проблем. Так, оставалось непонятным, откуда возникает субъективизм и релятивизм в эстетических оценках (типа "На вкус и цвет товарищей нет"), если прекрасное едино. Однако античное учение о мере и гармонии как объективных признаках прекрасного прошло через эпохи средневековья, Возрождения, Просвещения вплоть до наших дней, хотя происхождение красоты в каждую эпоху трактовалось по-своему. Во времена средневековья для философа Фомы Аквинского красота заключалась в боге, который "именуется прекрасным как причина гармонии и ясности". Как отголоски этой веры в божественное происхождение прекрасного сохранились выражения "ангельское лицо", "божественный голос", "чудесная погода". Для ренессансного гуманиста Альберти гармония есть "абсолютное и первичное начало природы". Французские просветители-материалисты также подчеркивали природную основу красоты.
С тех пор как в 1844 г. К. Маркс впервые высказался о "законах красоты" (см. с. 26), о них заговорили как о чем-то давно известном, не утруждая себя необходимостью раскрыть содержание этих законов. Между тем дальше того, что в данном вопросе эстетики разделились на два противоборствующих лагеря "природников" и "общественников", дело не пошло. Проблема законов красоты в эстетике скорее только поставлена, но не решена. Однако то, что законы меры и гармонии являются объективными законами прекрасного, по которым природа стихийно, а человек сознательно формируют материю, создавая совершенные формы, является бесспорным.
Остановимся несколько подробнее на эстетическом удержании законов симметрии, пропорциональности и гармонии как слагаемых прекрасного. Что касается закона ритма, который проявляется и в музыке, и в архитектуре, и в изобразительном искусстве, и в стихосложении, то он заслуживает отдельного разговора и в данной книге рассматриваться не будет.
4.1. Симметрия. Симметрия является фундаментальным свойством природы, представление о котором, как отмечал академик В. И. Вернадский (1863-1945), "слагалось в течение десятков, сотен, тысяч поколений". "Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло ее в рисунке и в предметах быта. Надо полагать, что применение симметрии в первобытном производстве определялось не только эстетическими мотивами, но в известной мере и уверенностью человека в большей пригодности для практики правильных форм". Это слова другого нашего замечательного соотечественника, посвятившего изучению симметрии всю свою долгую жизнь, академика А. В. Шубникова (1887-1970).
Первоначальное понятие о геометрической симметрии как о гармонии пропорций, как о "соразмерности", что и означает в переводе с греческого слово "симметрия", с течением времени приобрело универсальный характер и было осознано как всеобщая идея инвариантности (т. е. неизменности) относительно некоторых преобразований. Таким образом, геометрический объект или физическое явление считаются симметричными, если с ними можно сделать что-то такое, после чего они останутся неизменными. Например, пятиконечная звезда, будучи повернута на 72° (360°: 5), займет первоначальное положение, а ваш будильник одинаково звенит в любом углу комнаты. Первый пример дает понятие об одном из видов геометрической симметрии - поворотной, а второй иллюстрирует важную физическую симметрию - однородность и изотропность (равнозначность всех направлений) пространства. Благодаря последней симметрии все физические приборы (в том числе будильник) одинаково работают в разных точках пространства, если, конечно, не изменяются окружающие физические условия. Легко вообразить, бы царила на Земле неразбериха, если бы эта симметрия была нарушена!

Морская звезда - пример живого организма с поворотной симметрией 5-го порядка. Этот тип симметрии наиболее распространен в живой природе (цветы незабудки, гвоздики, колокольчика, вишни, яблони и т. д.) и принципиально невозможен в кристаллических решетках неживой природы. Симметрию 5-го порядка называют симметрией жизни. Это своеобразный защитный механизм живой природы против кристаллизации, против окаменения, за сохранение живой индивидуальности
Почти все утверждают, что красоту, воспринимаемую зрением, порождает соразмерность частей друг с другом и целым и с прелестью красок. И для тех, кто это утверждает, и вообще для всех остальных, быть прекрасным - значит быть симметричным и соразмерным.
Таким образом, не только симметричные формы окружают нас повсюду, но и сами многообразные физические и биологические законы гравитации, электричества и магнетизма, ядерных взаимодействий, наследственности пронизаны общим для всех них принципом симметрии. "Новым в науке явилось не выявление принципа симметрии, а выявление его всеобщности",- писал Вернадский. Действительно, еще Платон мыслил атомы четырех стихий - земли, воды, огня и воздуха - геометрически симметричными в виде правильных многогранников (см. гл. 7). И хотя сегодня "атомная физика" Платона кажется наивной, принцип симметрии и через два тысячелетия остается основополагающим принципом современной физики атома. За это время наука прошла путь от осознания симметрии геометрических тел к пониманию симметрии физических явлений.
Итак, в современном понимании симметрия - это общенаучная философская категория, характеризующая структуру организации систем. Важнейшим свойством симметрии является сохранение (инвариантность) тех или иных признаков (геометрических, физических, биологических и т. д.) по отношению к вполне определенным преобразованиям. Математическим аппаратом изучения симметрии сегодня является теория групп и теория инвариантов.
"Принцип симметрии в XX веке охватывает все новые области. Из области кристаллографии, физики твердого тела он вошел в область химии, в область молекулярных процессов и в физику атома. Нет сомнения, что его проявления мы найдем в еще более далеком от окружающих нас комплексов мире электрона и ему подчинены будут явления квантов".
Этими словами академика В. И. Вернадского и хочется закончить короткий разговор (который и так перерос рамки нашей темы) о всеобщности принципа симметрии. О симметрии написано огромное количество замечательных книг. Некоторые из них приведены в конце книги, в списке рекомендуемой литературы.

Ёмеймон (Ворота сияния солнца) - вход в комплекс погребального ансамбля Тосёгу в г. Никко. Япония. 1634-1636. Японская пословица гласит: 'Не говори кекко (чудесно), если ты не видел Никко!'

Отражение в воде - единственный пример горизонтальной симметрии в природе. Быть может, в этом и состоит тайна его очарования? Алтай. Озеро горных духов. Фото автора
Прежде чем перейти к еще одной грани симметрии - эстетической, следует сказать несколько слов о нарушении симметрии. Мы уже отмечали, что все физические законы являются симметричными. Но при ближайшем рассмотрении в каждой такой симметрии обнаруживается маленький изъян. Оказывается, природа не терпит точных симметрии! Природа почти симметрична, но не абсолютно симметрична! Так, планетные орбиты, которые еще Пифагором мыслились в виде совершенных окружностей, на самом деле оказались почти окружностями, но все-таки не окружностями, а эллипсами. Нарушение симметрии обнаружено во многих явлениях ядерной физики. Приблизительная симметрия является сегодня одной из научных загадок. Вот что по этому поводу пишет современный американский физик, лауреат Нобелевской премии Ричард Фейнман: "Почему природа столь близка к симметрии? По этому вопросу ни у кого нет никакой разумной мысли. Единственное, что я могу предложить вам,- это старое японское предание. В японском городе Никко есть ворота, которые японцы называют самыми красивыми воротами страны. Они были построены в период большого влияния китайского искусства. Это необычайно сложные ворота, со множеством фронтонов, изумительной резьбой и большим количеством колонн, на основании которых вырезаны драконьи головы, божества и т. п. Но, приглядевшись, можно заметить, что в сложном и искусном рисунке на одной из колонн некоторые из его мелких деталей вырезаны вверх ногами. В остальном рисунок полностью симметричен. Спрашивается: для чего это было нужно? Как говорит предание, это было сделано для того, чтобы боги не заподозрили человека в совершенстве. Ошибка была сделана намеренно, дабы не вызвать зависти и гнева богов.
Мы можем, вообще говоря, подхватить эту мысль и сказать, что истинное объяснение приблизительной симметрии мира состоит в следующем: боги сотворили свои законы только приближенно симметричными, чтобы мы не завидовали их совершенству!" Более серьезной "разгадки" тайны приближенной симметрии наука пока предложить не может.
Перейдем, наконец, к эстетическому содержанию симметрии, к ответу на толстовский вопрос: "почему симметрия приятна для глаз?" Видимо, господством симметрии в природе, о котором мы не случайно так много говорили, и объясняется прежде всего эстетическая ценность симметрии для человека. С детства человек привыкает к билатерально симметричным родителям, затем у него появляются билатерально симметричные друзья; он видит зеркальную симметрию в бабочках, птицах, рыбах, животных, поворотную - в стройных елях и волшебных узорах снежинок, переносную - в оградах парков, решетках мостов, лестничных маршах, бордюрах, которые издревле были любимым декоративным элементом. Человек привыкает видеть в природе вертикальные оси и плоскости симметрии, и вертикальная симметрия воспринимается нами гораздо охотнее. Мы нигде не увидим обои с горизонтальными осями симметрии, ибо это вызвало бы неприятный контраст с вертикальной симметрией растущих за окном деревьев. Единственная горизонтальная симметрия, которую мы встречаем в природе,- это отражения в зеркале воды. Возможно, в необычности такой симметрии и заключается ее завораживающая сила.
Таким образом, симметрия воспринимается человеком как проявление закономерности, порядка, царящего в природе. Восприятие же закономерного всегда доставляет нам удовольствие, сообщает некоторую уверенность и даже бодрость. "Порядок освобождает мысль",- любил повторять великий французский математик, философ и храбрый воин Рене Декарт (1596-- 1650). Его соотечественник, выдающийся зодчий XX века, авторитет, равного которому в архитектуре не было со времен Микеланджело, Ле Корбюзье (1887-1965) писал: "Человеку необходим порядок; без него все его действия теряют согласованность, логическую взаимосвязь. Чем совершеннее порядок, тем спокойнее и увереннее чувствует себя человек. Он делает умозрительные построения, основываясь на порядке, который продиктован ему потребностями его психики,- это творческий процесс. Творчество есть акт упорядочения".
Итак, симметрия, воспринимаемая человеком как закономерность структуры, как внешнее проявление внутреннего порядка, начинает обладать эстетической ценностью, т. е. воспринимается как красота. Простой пример убеждает в этом. Чернильная клякса сама по себе некрасива. Но стоит перегнуть лист бумаги с невысохшей кляксой пополам, и мы получим кляксу, которая уже производит приятное впечатление. Зеркальная симметрия новой кляксы, т. е. закономерное расположение ее частей, и определяет красоту нашей "рукотворной" кляксы. Знание законов геометрической симметрии сделает такие поиски быстрыми и плодотворными.
Чувство глубочайшего уважения к мощи законов симметрии никогда не ослабевает у того, кто обдумывал изящество и красоту безупречных математических доказательств и сопоставлял это со сложными и далеко идущими физическими и философскими следствиями.
На рисунке изображены узоры, полученные с использованием различных типов геометрической симметрии из простой, достаточно бесформенной кляксы. Узор на рисунке б получен с помощью зеркальной симметрии. Однако закон его построения слишком прост и очевиден, потому и эстетическая ценность такого узора невелика.
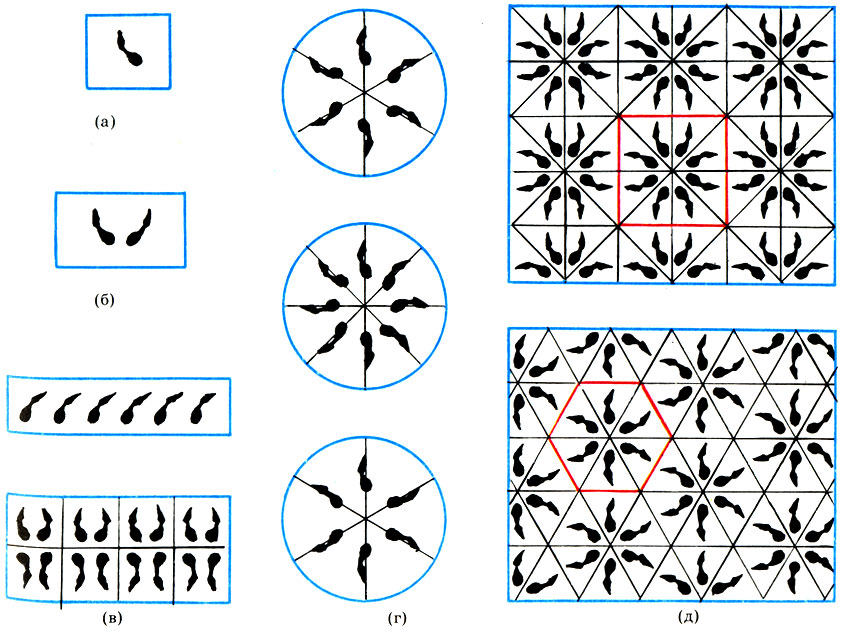
'Кляксография' - узоры, полученные из обыкновенной кляксы (а) с помощью зеркальной симметрии (б), переносной симметрии (в)у поворотной симметрии (г) и орнаментальной симметрии(d)
Узоры, приведенные на рисунке в, называются бордюрами и представляют собой тип переносной симметрии, когда каждая предыдущая фигура совпадает с последующей при поступательном перемещении вдоль бордюра на постоянный интервал (шаг симметрии). Нижний бордюр имеет более сложный закон построения, чем простая переносная симметрия. Всего же существует семь типов бордюров.
На рисунке г показаны так называемые "розетки". Розетки получаются поворотом фигуры вокруг вертикальной оси на угол 360°/n (n = 2, 3, 4, ...), т. е. обладают поворотной симметрией n-го порядка. (Верхняя розетка имеет поворотную симметрию 6-го порядка, средняя - 8-го, нижняя же сочетает зеркальную и поворотную симметрии, но в то же время она имеет чисто поворотную симметрию 3-го порядка.)
Наконец, на рисунке д показаны два орнамента из семнадцати возможных. Орнаментальная симметрия строится на одной из пяти возможных плоских решеток. Верхний орнамент имеет квадратную решетку, а нижний - гексагональную (правильный шестиугольник). Заполнив одну ячейку решетки, мы получим с помощью переносной симметрии весь орнамент.
Вот так с помощью симметрии простая клякса превращается в затейливые узоры, которые уже никак не назовешь некрасивыми. Нам нравится вглядываться в узоры симметрии, постигать их законы, и они воспринимаются нами как красивые. "Смысл эстетического воздействия симметрии (и всякой иной закономерности), по нашему мнению,- писал Шубников,- заключается в том психическом процессе, который связан с открытием ее законов".
Другим важным фактором, составляющим эстетическое содержание симметрии, является ее целесообразность, которая также есть проявление закономерного. Уже первобытные люди понимали, что симметричные орудия более целесообразны, чем несимметричные. Таким образом, уже в эпоху неолита симметрия была выделена как наиболее совершенная форма, о чем свидетельствуют многочисленные украшения с симметричными рисунками.
Современный человек просто не в состоянии представить себе несимметричный (а значит, и нефункциональный) самолет или автомобиль. В этой связи показательны наблюдения известного летчика-испытателя, Героя Советского Союза Марка Галлая: "Я заметил, что красивая, ласкающая своими пропорциями взор машина обычно к тому же и хорошо летает. Эта, на первый взгляд, почти мистическая закономерность имеет, я думаю, свое вполне рациональное объяснение: дело, по-видимому, обстоит как раз наоборот - хорошо летающая машина начинает представляться "красивой". Эстетическое формируется под влиянием рационального".

Симметрия, пропорция, гармония - слагаемые прекрасного
Итак, целесообразность симметричных форм была осознана человечеством в доисторические времена, а в сознании древних греков симметрия стала олицетворением закономерности, целесообразности, а следовательно, и красоты. Идея связи прекрасного с симметрией пронизывала всю греческую философию, все греческое искусство. Достаточно вспомнить строго симметричные формы античных архитектурных памятников, изумительную стройность греческих ваз, математическую строгость их орнамента. С тех пор симметрия и красота в сознании человека слиты воедино. В "Фаусте" Гёте противопоставляет в образах Прекрасной Елены и одноглазой, однозубой старухи Форкиады красоту симметрии и уродство асимметрии. В "Сказке о царе Салтане" Пушкин рисует величавую Царевну-Лебедь со звездой во лбу (красота-симметрия) и окривевших злодеек ткачиху с поварихой (уродство-асимметрия). В "Войне и мире" Льва Толстого мы читаем: "Это был огромный, в два обхвата, дуб, с обломанными, давно видно, суками и с обломанной корой, заросшей старыми болячками. С огромными своими неуклюже, несимметрично растопыренными корявыми руками и пальцами, он старым, сердитым и презрительным уродом стоял между улыбающимися березами".
Симметрия как объективный признак красоты проходит через всю историю искусств. "Равенство, неравенство, повторение и симметрия, определенные структуры играют в искусстве, как и в математике, фундаментальную роль",- считает физик Гейзенберг. Не говоря уже об архитектуре и скульптуре, симметрия господствует в изобразительном искусстве Древнего Египта, Древней Греции и Рима, средневековья и Возрождения. Зеркальная симметрия была особенно излюблена шумерами.

Симметрия в искусстве. Зеркальная симметрия: нагрудное украшение с именем фараона. XX в. до н. э. (а)

Симметрия в искусстве. Зеркальная симметрия: капитель колонны из дворца Артаксеркса II в Сузах. V-IV вв. до н. э. (б)

Поворотная симметрия 12-го порядка: мозаика купола баптистерия в Равенне. V в. (в)

Переносная симметрия: рельефы ападаны в Персеполе. VI-V вв. до н. э. (г)
Симметрия в искусстве - это волнующая тема, которая заслуживает особого разговора. Поэтому мы ограничимся только замечанием о том, что следование принципу зеркальной симметрии в искусстве иногда приводило к парадоксальным результатам. Так, на мозаике Киевского собора св. Софии под знаменитой Орантой изображены два зеркально-симметричных Христа, обращенных лицом к ученикам. Правда, при ближайшем рассмотрении мы увидим, что симметрия здесь лишь приблизительная, так как один Христос преломляет хлеб, а другой разливает вино. Этот прием, позволяющий одновременно изобразить два важнейших момента тайного причастия, безусловно, является слишком "математичным" и со временем был вытеснен более реалистическим изображением тайной вечери.
Как и в любом деле, абсолютизация одной идеи не могла привести ни к чему хорошему. Симметрия в искусстве не составила исключения. "Красота неправильная", асимметрия, стала пробивать себе дорогу в искусстве, ибо сведение красоты только к симметрии ограничивало богатство ее внутреннего содержания, лишало красоту жизни. Истинную красоту можно постичь только в единстве противоположностей. Вот почему именно единство симметрии и асимметрии определяет сегодня внутреннее содержание прекрасного в искусстве. Симметрия воспринимается нами как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность.

Евхаристия. Мозаика апсиды собора Св. Софии в Киеве. 1043-1046. Зеркально-симметрическое раздвоение фигуры Христа позволяло одновременно изображать два важнейших момента евхаристии: причащение хлебом, символизировавшим тело Христово, и причащение вином, обозначавшим кровь Христа. Зеркальное раздвоение Христа было одним из излюбленных приемов в иконографии тайной вечери

Покровский собор на Рву - храм Василия Блаженного. Москва. 1555-1560. Зодчие Барма и Постник. Гармоническое сочетание симметрии частей и асимметрии целого
Примером удивительного сочетания симметрии и Симметрии является Покровский собор (храм Василия блаженного) на Красной площади в Москве. Эта причудливая композиция из десяти храмов, каждый из которых обладает центральной симметрией, в целом Не имеет ни зеркальной, ни поворотной симметрии. Симметричные архитектурные детали собора кружатся в своем асимметричном, беспорядочном танце вокруг его центрального шатра: они то поднимаются, то опускаются, то как бы набегают друг на друга, то отстают, создавая впечатление радости и праздника. Без своей удивительной асимметрии храм Василия Блаженного просто немыслим!
Итак, "сфера влияния" симметрии (а значит, и ее антипода - асимметрии) поистине безгранична. Природа - наука - искусство. Всюду мы видим противоборство, а часто и единство двух великих начал - симметрии и асимметрии, которые во многом и определяют гармонию природы, мудрость науки и красоту искусства.
4.2. Пропорция. Слово "пропорция" ввел в употребление Цицерон в I веке до н. э., переведя им на латынь платоновский термин "аналогия", который буквально означал "вновь-отношение", или, как мы говорим, "соотношение". С тех пор вот уже 2000 лет пропорцией в математике называют равенство между отношениями четырех величин а, b, с, d:
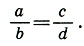 (4.1)
(4.1)Пропорция в искусстве также определяет соотношение величин элементов художественного произведения либо соотношение отдельных элементов и всего произведения в целом. В эстетике пропорция, как и симметрия, является составным элементом категории меры и выражает закономерность структуры эстетического образа.
Издревле в пропорции художники видели объективную основу красоты, по крайней мере формы прекрасного. Не все художники желали рассматривать искусство лишь как плод безудержной фантазии и чистой интуиции. И те из них, кто пытался постигнуть объективные законы прекрасного, находили их прежде всего в пропорции.
Мы уже отмечали, что симметрия воспринимается слишком статично, скованно и только единство симметрии и асимметрии создает подлинную гармонию красоты. Так вот, в качестве меры соотношения симметричного и асимметричного часто и выступает пропорция. Возьмем простой пример: деление отрезка прямой. Если отрезок разделить пополам, зеркально-симметрично, то такое деление выглядит уравновешенным, мертвым. Если же точку деления взять слишком близко к одному из концов отрезка, то новая конфигурация будет чересчур неуравновешенной и беспокойной. Только некоторая "золотая середина", которая в данном случае отнюдь не является геометрической серединой, обеспечит йам желаемое единство симметрии и асимметрии.

Симметрия, пропорция, гармония - слагаемые прекрасного
Такое "радующее глаз" деление отрезка, по преданию, было известно еще Пифагору и называлось им золотой пропорцией. Впрочем, скорее всего золотая пропорция была заимствована Пифагором у древних египтян, которые знали ее задолго до Пифагора и которых он посетил в своих странствиях по свету. Золотая пропорция определяется как деление отрезка на две неравные части, при котором меньшая из них так относится к большей, как последняя ко всей длине отрезка. С тех пор золотая пропорция становится общепризнанным каноном искусства. Художник и инженер Леонардо да Винчи, изучавший и восхвалявший золотую пропорцию на протяжении всей своей жизни, называет ее "Sectio aurea" (золотое сечение), а математик и астроном Иоганн Кеплер, обнаруживший золотую пропорцию в ботанике, говорит о ней как о бесценном сокровище, как об одном из двух сокровищ геометрии* и именует ее "Sectio divina" (божественное сечение). Название Леонардо да Винчи сохранилось и сегодня.
*(К другому "геометрическому сокровищу", по мнению еплера, относилась теорема Пифагора.)
Последующие научные открытия показали, что золотое сечение составляет основу многих природных явлений, что оно связано с глубокими естественнонаучными закономерностями. Таким образом, будучи мерой, законом природы, золотое сечение становится и мерой человеческого творчества, "законом красоты": совершенная природа дает человеку образец совершенства. Так раскрывается еще одна эстетическая грань золотого сечения - целесообразность, ибо в целесообразности природы сомнений у человечества никогда не было.
Гармония мира. Иллюстрация из книги итальянского теоретика музыки . Ф. Гафурио 'Практика музыки'. Милан. 1498
Золотое сечение мы находим всюду: в изобразительном и прикладном искусстве, в архитектуре и музыке, в литературе, в предметах быта и машинах. Многочисленные исследования показали, что на точке золотого сечения обычно бывает кульминация в поэтических, драматургических и музыкальных произведениях (см. с. 164). Золотое сечение мы находим в общей композиции произведения и в соотношении его частей. Не менее удивительно и то, что золотое сечение мы находим всегда, в совершенно различных цивилизациях, отделенных друг от друга тысячелетиями: в усыпальнице Хеопса в Древнем Египте и в храме Парфенон в Древней Греции, в Баптистерии эпохи Возрождения в Пизе и в храме Покрова на Нерли, в ленинградском Адмиралтействе и в ультрасовременных сооружениях Ле Корбюзье. Золотое сечение мы обнаруживаем и в музыкальных шедеврах Баха, Моцарта, Вагнера, Шопена, Глинки, и в поэтических произведениях от Лермонтова до Вознесенского.
Загадка притягательной силы золотого сечения давно волнует человечество. Были и чисто математические "доказательства" эстетического предпочтения человеком золотого сечения, были и физиологические, связанные, например, со спецификой сокращения глазных мышц. Нам представляется наиболее правдоподобным наиболее простое объяснение: эстетическое превосходство золотого сечения является не врожденным, а "благоприобретенным" в процессе исторического развития человечества. Поскольку золотое сечение дано человеку самой природой в пропорциях его же тела, оно постепенно и стало для него идеалом красоты. Эту мысль подтверждает и эстетическое "равнодушие" детей к золотому сечению, проверенное экспериментально.
Эстетике и математике золотого сечения мы посвятили отдельную главу (гл. 15). Здесь же мы отметим, что золотое сечение было не единственным каноном пропорциональности в искусстве. Например, готическая архитектура основана на совершенно иной системе пропорций, а английский художник и эстетик XVIII века Уильям Хогарт (1697-1764) в своем трактате "Анализ красоты" призывал к использованию асимметричных "змеевидных" линий, позволяющих воспроизвести жизнь во всем ее многообразии. Хогарт нашел даже особую "линию красоты" - плавную синусоидальную кривую, которая, согласно его взглядам, выражала сущность прекрасного. Впрочем, различным системам пропорциональности посвящена фактически вся третья часть нашей книги, ибо архитектура как искусство во многом определяется принятой системой пропорциониро-вания. Поэтому мы не будем более останавливаться на пропорции и перейдем к следующему слагаемому прекрасного - гармонии.
4.3. Гармония. Идея Гармонии, как антитеза идеи Хаоса, имеет тысячелетнюю традицию: Хепри и Нун в космологических мифах Древнего Египта, Сат и Асат в гимнах Ригведы, Ин-Ян и Дао в книгах даосских мудрецов, Свет и Тьма в Библии, Космос и Хаос в поэмах Гесиода и Гомера. Несмотря на множество вариантов и оттенков, а порой и отличий между этими двумя величайшими смыслообразами двух великих культур - Востока и Запада, их объединяла единая йдеЯ - идея безмерной пучины первобытия, рождающей в своих клокочущих недрах светлый луч гармония жизни. Эту древнейшую в истории мировой культуры идею не поглотили тысячелетия, и сегодня она ясно видна - будь то в последней мандале Ригведы:
Мрак был сокрыт мраком вначале. Неразличимая пучина - все это. То жизнедеятельное, что было заключено в пустоту, Оно одно было порождено силой жара.
или в первых строках Библии:
В начале сотворил Бог небо и землю. Земля же была безвидна и пустота, и тьма над бездною, и Дух Божий носился над водою.
Воистину идея хороша, когда она древна.
Но истинная древность всегда современна. И удивившись единожды почтенному возрасту древней идеи, сохраненной, словно засушенный цветок, в хрупких фолиантах мировых религий, мы удивляемся дважды, встречая ее расцветшей в самых современных научных теориях.
Конец XX века знаменуется бурным развитием статистической теории неравновесных процессов в физических, химических и биологических системах, созданной прежде всего благодаря усилиям нашего соотечественника Нобелевского лауреата Ильи Пригожина и его Брюссельской школы. На наших глазах теория неравновесных процессов перерастает во всеобъемлющую теорию изменения, имеющую самые широкие мировоззренческие следствия.
Суть этой теории в сильно упрощенном виде состоит в том, что в открытых системах, т. е. системах, обменивающихся с окружающей средой энергией и веществом и составляющих основу всего мироздания, возникают процессы самоогранизации, т. е. процессы, в ходе которых из физического хаоса рождаются некоторые структуры.

Симметрия, пропорция, гармония - слагаемые прекрасного
Таким образом, в конце XX века обретает свое второе рождение древняя библейская идея о возникновении Гармонии из Хаоса. В строгой естественно-ручной теории вновь оживают древние ведические Истины, звонко прозвучавшие в начале XX века в авторизованных переводах Константина Бальмонта:
Там не было ни Смерти, ни Бессмертья, Меж Днем и Ночью не было черты. Единое оно, само собою, Дышало без дыхания везде.
И поэтому сказано не без причины - все слагающееся из противоположностей объединяется и сочетается некоей гармонией. Ибо гармония есть единое многого и согласие разногласного.
Все было Тьмой, все покрывал сначала Глубокий мрак, был Океан без света. Единая пустынность без границ. Зародыш, сокровенностью объятый. Из внутреннего пламени возник.
Греческому слову "гармония" по крайней мере три тысячи лет, и за это время оно прошло столь же сложный путь развития, как и вся история человечества. Впервые оно встречается в поэмах легендарного поэта Древней Греции Гомера "Илиаде" и "Одиссее", датируемых IX-VII веками до н. э. В "Илиаде" "гармония" означает "мир, согласие", а в "Одиссее" - "скрепы, шипы", с помощью которых Одиссей соединял различные части строящегося корабля:
Двадцать он бревен срубил, их очистил, их острою медью Выскоблил гладко, потом уровнял, по снуру обтесавши. Тою порою Калипсо к нему с буравом возвратилась. Начал буравить он брусья и, все пробуравив, сплотил их, Длинными болтами сшив и большими просунув шипами.
С последующим ростом культуры, развитием философии и расширением языка науки понятие "гармония", сохраняя свое древнее значение "соединения, согласия", приобрело более глубокий и широкий смысл и стало важнейшей философской и эстетической категорией. Сегодня гармония в философии и эстетике означает соразмерность частей и целого, слияние различных компонентов объекта в единое органическое целое.
Гармония проявляется всюду, начиная от строения Солнечной системы и кончая духовной жизнью человека и общества. Чем сложнее целостная система, тем содержательнее оказывается гармония, выражающая соотношение противоречивых элементов. Кроме того, гармония стала обозначать один из разделов теории музыки, изучающий выразительные средства музыки, основанные на закономерном объединении музыкальных звуков в созвучия (аккорды) и на связи созвучий при их последовательном движении.
Учение о гармонии лишь немногим моложе самого слова. Оно возникло в VI веке до н. э. в трудах Пифагора и его учеников, пифагорейцев. Для пифагорейцев гармония означала организованность вселенной, она противостояла хаосу и определяла устройство всего мироздания.
В пифагорейском взгляде на гармонию, как изоморфное единство разнокачественных начал, нашла отражение глубокая убежденность древних в едином закономерном и рациональном устройстве мироздания. Идея гармонии, как всепроникающего единства разнородных и разнообразных начал, была доведена в пифагорейской философии до своего апогея - идеи внутреннего единства двух полярных высокоорганизованных миров: Микрокосма и Макрокосма. Апофеозом пифагорейской концепции гармонии стал знаменитый античный тезис: "Познай самого себя, и ты познаешь Богов и Вселенную".
Но что является сущностью, носителем гармонии? Уже в античную эпоху по этому вопросу имелись разногласия. Пифагорейцы считали, что в основе гармонии мироздания лежат число, числовые пропорции и отношения. Это было вполне оправдано, ибо, с одной стороны, числа тесно связаны с реальным миром, в котором все поддается счету, а с другой - они существуют как бы отдельно от него, чужды земному хаосу, суете и тлену. Открытие же связи между числом и музыкой, между мудростью числа и красотою музыки, укрепило пифагорейцев в своих воззрениях: гармония мироздания виделась им в математических соотношениях.
Иное дело - Гераклит, видевший в основе всего, в том числе и гармонии, борьбу противоположностей. "Борьба - отец всего и царь всему",- учил Гераклит. Гераклит впервые высказал мысль о двух видах гармонии - "скрытой" и "явной". По Гераклиту, скрытая гармония лежит в основе красоты и совершенства Космоса и, безусловно, сильнее явной гармонии. "И если мир,- говорит Гераклит,- кажется кучей мусора, рассыпанного наудачу, то здесь за игрой стихийных сил и случайностей скрывается прекраснейшая гармония". Ту же мысль через две с половиной тысячи лет высказал в поэтической форме А. Блок:
Сотри случайные черты - И ты увидишь: мир прекрасен.
Гармония Пифагора и гармония Гераклита не взаимоисключают, а взаимодополняют друг друга: первая - как единство разнокачественных начал - по своему содержанию ближе к мирозданию, вторая - как единство взаимоисключающих противоположностей - ближе к искусству. Таким образом, со времен Пифагора и Гераклита концепция гармонии мироздания и гармонии искусства развиваются в тесной взаимосвязи, а сам термин гармонии одинаково близок и дорог как ученым, так и художникам.
Душа следует своим собственным законам, тело - также своим, и они сообразуются в силу гармонии, предустановленной между всеми субстанциями, так как они все суть выражения одной и той же вселенной.
Зерна учения о гармонии, брошенные Пифагором а Гераклитом в благодатную почву средиземноморской культуры, проросли в могучее древо гармонии, своими корнями сплотившее воедино все интеллектуальное наследие человечества. Учение о гармонии было подхвачено и развито Платоном, чья философия, будто скрепы-гармонии одиссеева корабля, пронизывает не только мировую философию, но и мировую культуру. Платон придал понятию гармонии универсальный смысл, распространив космологическую и математическую теории гармонии пифагорейцев на нравственный и духовный космос человека.
Гармония для Платона есть основа прекрасного. В свою очередь такие качества как мера, симметрия, пропорция составляют единое целое гармонии. Из этих посылок естественным образом вытекает знаменитое изречение Платона о том, что "умеренность и соразмерность всюду становится красотой и добродетелью".
Начиная с ранней классики взгляд на гармонию как согласие разногласного, лежащее в основе мироздания, как путеводную звезду на пути к тайнам мироздания отличается завидным постоянством. Такой взгляд на гармонию сохранял и в эпоху позднего эллинизма Цицерон: "Только мир свободен от всяких недостатков и во всех своих пропорциях и частях строен, закончен и совершенен"; и в последних лучах догоравшей античной культуры Боэций: "И поэтому сказано не без причины - все слагающееся из противоположностей объединяется и сочетаемся некоей гармонией"; и на рассвете эпохи Возрождения Альберти: "Ведь назначение и цель гармонии - упорядочить части, вообще говоря, разные по природе, неким совершенным отношением так, чтобы они одна другой соответствовали, создавая красоту"; и на пороге века Просвещения Лейбниц: "Душа следует своим законам, тело - также своим и они сообразуются в силу гармонии, предустановленной между всеми субстанциями, так как все они суть выражения одной и той же вселенной"; и в начале XX в. Пуанкаре: "Но то, что мы называем объективной реальностью, в конечном счете есть то, что .общо нескольким мыслящим существам и могло бы быть общо всем. Этой общею стороной может быть только гармония, выражаемая математическими законами. Следовательно, именно эта гармония и есть единственная объективная реальность, единственная истина, которой мы может достигнуть; а если я прибавлю, что универсальная гармония мира есть источник всякой красоты, то будет понятно, как мы должны ценить те медленные и тяжелые шаги вперед, которые мало-помалу открывают ее нам"; и в середине XX в. Эйнштейн: "Без веры во внутреннюю гармонию нашего мира, не могло бы быть никакой науки. Эта вера есть и всегда останется основным мотивом всякого научного творчества".
К сожалению, у нас нет возможности остановиться подробнее на развитии учения о гармонии, в котором, как в капле воды, отражается все развитие человеческой мысли. Аристотель и Секст Эмпирик, Августин и Фома Аквинский, Дюрер и Леонардо да Винчи, Кеплер и Галилей, Гете и Шиллер, Кант и Гегель, Гейзенберг и Шредингер внесли свой вклад в это древнейшее учение.
Мы же отметим три важных аспекта, которые выделяют в современных воззрениях на гармонию,- математический, эстетический и художественный. На ранних этапах развития учения о гармонии господствовало ее математическое понимание. Гармония трактовалась как соразмерность, пропорциональность отдельных частей, а также частей и целого. Такое внешнее, формальное толкование гармонии, выделяющее прежде всего количественную математическую сторону, было характерно Для пифагорейцев и мыслителей средневековья. В XVII веке пифагорейские "математические" взгляды на гармонию поднял на щит Иоганн Кеплер.
В эпоху Возрождения математическое понимание гармонии постепенно вытесняется эстетическим. В отличие от математического эстетическое понимание гармонии является не просто количественным, а качественным, выражающим внутреннюю природу объекта. В эстетическом понимании гармонии получает развитие мысль Платона о связи гармонии с прекрасным. Поэтому эстетическая гармония связывалась с эстетическим еРезкиванием, с чувством прекрасного. В европейской этике красота природы становится неотделимой от РеДставления о ее гармонии.
Ле Корбюзье. Эскиз капеллы в Роншане
Более глубокое и диалектическое - художественное понимание гармонии вырабатывается в эстетике нового времени. Художественная гармония - это гармония искусства, это не только математическое соответствие между однородными элементами, но и единство противоположных эстетических категорий: прекрасного и безобразного, трагического и комического, возвышеного и низменного. Благодаря единству и борьбе этих противоречивых категорий художественная гармония приобретает движение и наполняется жизнью.
Итак, гармония - это сложное и многозначное понятие; поэтому гармония так близка и естествоиспытателю, и философу, и художнику.
Вот почему современные физики так часто говорят о гармонии природы, искренне веря, что сердцевину мироздания составляют простые и красивые математические закономерности и формулы. "Восприняв от античности идею о математическом истолковании порядка в природе,- пишет В. Гейзенберг,- современное естествознание осуществляет ее, однако, другим... способом... Наука нового времени показала, что в окружающем нас реальном мире неизменными являются не геометрические формы, а динамические законы... Гармонию пифагорейцев, которую еще Кеплер надеялся найти в орбитах небесных светил, естествознание со времен Ньютона ищет в математической структуре законов динамики, в уравнениях, формулирующих эти законы".
Вот почему художники так боготворят гармонию. "Поэт - сын гармонии,- говорил в своей речи "О назначении поэта" А. Блок,- и ему дана какая-то роль в мировой культуре. Три дела возложены на него: во-первых, освободить звуки из родной безначальной стихии, в которой они пребывают; во-вторых, привести эти звуки в гармонию, дать им форму; в-третьих, внести эту гармонию во внешний мир".
Поиски скрытой гармонии - высший удел и ученых, и художников. Это вечный путь человеческой культуры, путь, приносящий и ученым, и художникам муки и радости. А в конце пути, когда "ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже", сияет недосягаемая вершина - Гармония.
О трудном пути к этой вершине писано немало. Писал о нем и русский художник В. И. Суриков: "А какое время надо, чтобы картина утряслась так, чтобы переменить ничего нельзя было. Действительные размера каждого предмета найти нужно. Важно найти замбк" чтобы все части соединить. Это - математика". Имени0 математике, лежащей в основе скрытой гармонии искусства, и посвящены следующие три части книги.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'