9. Задача Эйлера о семи мостах и другие задачи

"На груди его красовался Орден Семи Мостов самого первого класса (рис. 10).

Рис. 10

- Темные места,- объяснил доктор,- представляют собой речку, а белые дорожки - это берега речки и мосты. Задача очень простая: обойти все мосты и по каждому пройти только один раз. Знаешь ли ты, что это за речка?

- Нет,- промолвил Илюша.- А разве есть на самом деле такая речка?

- Есть! Это речка Преголя с островом, а на ней стоит город Калининград... Эти мосты оказались причиной возникновения очень важной отрасли геометрии... Однажды на одном вечере в обществе кто-то задал Эйлеру вопрос: можно ли пройти по этим семи мостам, не проходя ни по одному два раза? Эйлер заинтересовался этой задачей, доказал, что сделать это невозможно, и нашел общие правила, которым подчиняются задачи подобного рода. В честь этого замечательного события и учрежден этот превосходный и достопримечательный орден".

Разумеется "орден" - фантазия Сергея Боброва, автора популярной математической книги "Волшебный двурог", откуда и заимствован с некоторыми сокращениями приведенный выше отрывок. Но частная задача о семи мостах действительно рассматривалась Эйлером и послужила первопричиной весьма общих открытий.

В самом деле: так ли уж важно пройти по каждому из мостов ровно один раз? Что за беда, если путешественник пропустит какой-либо мост или пройдет по мосту дважды?

Обобщение результатов рассмотрения какой-либо конкретной задачи нередко приводит к открытию общих закономерностей, правил, формул. Увидеть в частной, иногда очень простой задаче важную общую проблему и решить эту проблему - доступно немногим. Одним из таких немногих был крупнейший математик XVIII в. Леонард Эйлер.

Эйлер обратил внимание на математическую сущность некоторых задач, связанных с шахматной доской. Одна из таких задач состоит в определении маршрута коня, который должен обойти все 64 поля шахматной доски, побывав на каждом поле только один раз.

(Напоминаем: конь ходит буквой "Г"; на рис. 11 отмечены все поля, на которые конь может пойти своим ближайшим ходом.)

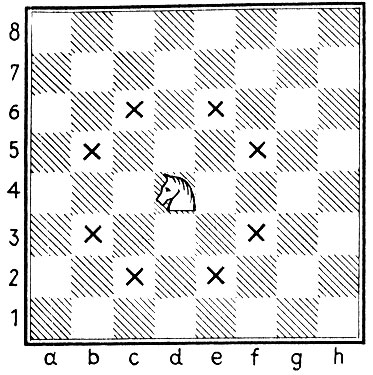
Рис. 11

Найти какой-нибудь из требуемых маршрутов не так уж сложно. При достаточном терпении с этим справится любой из наших читателей. На рисунке 12 показана одна из возможных последовательностей посещения конем всех полей шахматной доски. Сложнее другое: определить количество различных маршрутов.

Рис. 12

Задача имеет богатую событиями историю. Ее решением занимались многие математики нескольких предыдущих столетий. Однако Эйлер впервые обратил внимание на ее математическую сущность.

Полностью решить задачу - определить точное число маршрутов - пока не удалось. Известно количество различных маршрутов для половины шахматной доски, т. е. для доски 8*4. Известно, что общее число маршрутов на всей доске не менее 31 054 144, но менее числа С⁶³₁₆₈ (это число порядка 10¹⁰⁰).

Профессор Дерптского (ныне г. Тарту, Эст. ССР) университета Фердинанд Миндинг (1806-1885) указал возможный метод подсчета количества маршрутов. Однако объем необходимых работ для его осуществления настолько велик, что выполнить его практически пока не удалось даже с помощью ЭВМ. Поэтому метод Миндинга представляет лишь теоретический интерес, показывая принципиальную возможность решения задачи.

В другой задаче требовалось расставить на доске размером n*n клеток n ладей так, чтобы ни одна из них не могла бить другую.

Ладья в шахматах ходит и бьет по горизонтали и по вертикали (рис. 13). Задача сводится к тому, чтобы на каждой горизонтали выбрать разные вертикали (или, наоборот, на каждой вертикали выбрать разные горизонтали). Если обозначить поля, занимаемые ладьями,

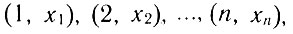
то существует ровно n! различных порядков расположения чисел х₁, x₂, . . . х_H. Поэтому, на обычной шахматной доске 8*8 клеток существует ровно 8! = 40 320 различных решений задачи.

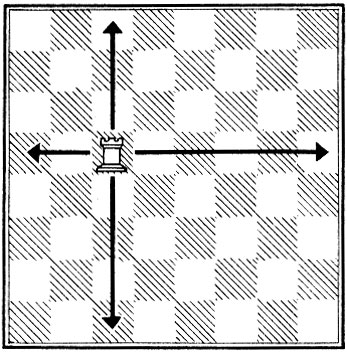
Рис. 13

Эйлеру предложили эту задачу в усложненной форме: было дополнительно запрещено ставить ладьи на главной диагонали, т.е. на поля a₁, b₂,...n₈; задачу требовалось решить в общем виде, для доски размером n*n клеток.

Эйлер не смог найти общую формулу, выражающую количество решений в виде функции от n. Однако, обозначив искомое количество решений через Q_n, Эйлер нашел рекуррентное соотношение

(*)

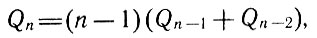которое позволяет постепенно найти количество решений для любого конкретного значения n.

Нетрудно убедиться, что для доски 2*2 существует единственное решение задачи (рис. 14), т. е. Q₂ = 1. Простой перебор вариантов показывает, что для доски 3*3 можно найти 2 решения (рис. 15), т.е. Q₃ = 2. Следовательно,

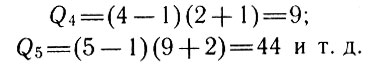
Рис. 14

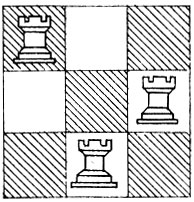
Рис. 15

Рис. 15

Общая формула решения задачи, найденная уже в XIX в., оказалась следующей

(**)

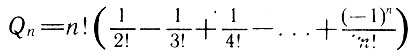и, в частности, для обычной доски 8*8

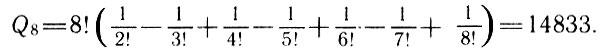
Проверку формулы (**) методом математической индукции с помощью соотношения (*), выведенного Эйлером, мы предоставляем читателю.

Занимаясь обобщением подобных задач, Эйлер вывел ряд важных соотношений между бесконечными суммами и бесконечными произведениями, которые оказались полезными в теории чисел, в том числе равенство.

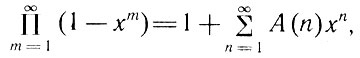
где символ 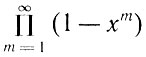означает произведение

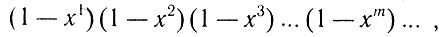
а символ 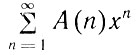означает сумму

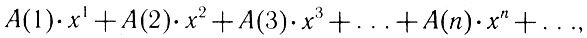
причем символ А(n) равен (-1)^k для целых чисел вида

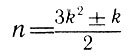
и равен нулю для всех остальных чисел.

Эйлер понимал также, что самое лучшее объяснение правила, самое подробное доказательство простейшей теоремы может оказаться не понятым без рассмотрения иллюстрирующих примеров, частных задач и упражнений. Поэтому учебные книги Эйлера содержат немало примеров, задач и упражнений. В заключение мы приведем две задачи, предлагавшиеся Эйлером.

- Мул и осел несли груз весом в несколько сотен каких-то единиц. Осел, жалуясь на свою судьбу, сказал мулу: "Мне нужно только сто единиц твоей ноши, чтобы я был нагружен вдвое тяжелее тебя". Мул возразил: "Да, верно, но если бы ты отдал мне сто единиц из твоей ноши, я был бы нагружен втрое больше тебя". Сколько единиц груза нес осел и сколько - мул?

- Отец после смерти оставил несколько детей, доля которых при разделе наследства выразилась так:

первый получил сто крон и одну десятую остатка;

второй получил 200 крон и одну десятую следующего остатка;

третий получил 300 крон и одну десятую следующего остатка

и т. д.

В конце концов наследство оказалось поделенным поровну между всеми детьми. Как велико было наследство и сколько крон получил каждый?