8. Основы вариационного исчисления

Каждому знакома простейшая кривая - окружность. В школе рассматриваются еще парабола, гипербола, синусоида и другие

кривые, а также их уравнения 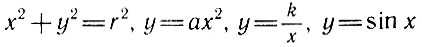и тому подобные уравнения, связывающие две переменные х и у. Впрочем, можно записывать уравнения и в параметрической форме; мы видели, что для окружности

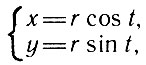
где параметр t - угол поворота вектора по отношению к положительному направлению оси абсцисс (см. рис. 6.). Каждая точка любой из этих кривых лежит в плоскости чертежа. Вспомните теперь винтовую линию (рис. 7). Если провести плоскость через какие-нибудь три ее точки, например через точки А, В и С, то всегда найдутся еще другие точки винтовой линии, не лежащие в этой плоскости. Винтовая линия не является плоской кривой; чтобы записать ее аналитически, понадобятся два уравнения с тремя переменными х, у и z, например

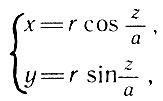
или, в параметрической форме,

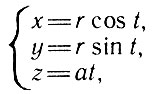
где 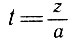- угол поворота переменного вектора по отношению к положительному направлению оси абсцисс, r - радиус выбранного цилиндра, на который "нанесена" винтовая линия, а - коэффициент, характеризующий "крутизну" винтовой линии.

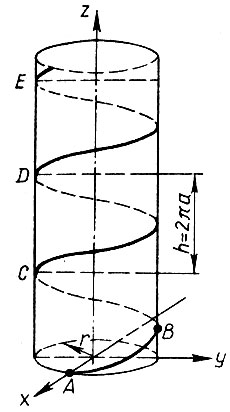
Рис. 7

Если развернуть поверхность цилиндра на плоскость, то винтовая линия также развернется и превратится в семейство наклонных отрезков (рис. 8). Крутизну развернутой винтовой линии можно охарактеризовать углом или, лучше, тангенсом угла а, составленного этими отрезками с разверткой основания цилиндра.

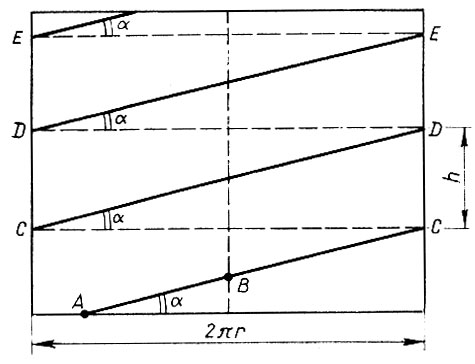
Рис. 8

Кратчайшим расстоянием между двумя точками А и В на плоскости является отрезок прямой, соединяющий эти точки. Ну, а если часть плоскости, на которой расположен отрезок АВ, искривить, превратить в поверхность цилиндра или конуса? Очевидно, кратчайшим расстоянием между точками А и В на этой поверхности будет тот же отрезок - теперь он будет проходить по геодезической линии на этой поверхности. Поэтому геодезической линией на поверхности цилиндра и будет отрезок винтовой линии. Если же говорить о геодезической линии, соединяющей две точки на сфере (шаровой поверхности), то это будет дуга большого круга - круга, радиус которого равен радиусу самого шара. Поэтому, например, корабли в открытом море и самолеты в воздухе движутся обычно именно по дугам больших кругов.

Задача найти геодезические линии на заданных поверхностях была поставлена еще Иоганном Бернулли. В 1728 г. он сообщил об этой задаче в письме к своему сыну Даниилу, а тот предложил ее Эйлеру, который в 1729 г. написал сочинение "О кратчайшей линии на поверхности, соединяющей две любые точки" (опубликовано в 1732 г.).

Задачу, поставленную Иоганном Бернулли, можно было решить чисто механически: овеществить нужную поверхность, скажем, в металле и на выпуклую ее сторону натянуть гибкую нить, закрепленную в двух указанных точках. Эйлер же решает задачу аналитически: вводит систему пространственных координат и разъясняет, что поверхность выражается одним уравнением с тремя переменными (ныне мы сказали бы: с тремя координатами х, у и z), линия - парой таких уравнений, точка - тройкой уравнений или просто тремя координатами х, у, z. Далее Эйлер решает задачу методами дифференциального исчисления в общем виде, а затем рассматривает применение найденного решения к частным видам поверхностей и, между прочим, доказывает, что при развертке цилиндра или конуса на плоскость любая геодезическая линия переходит в прямую.

В 1732 г. Эйлер пишет новое сочинение, рассматривает задачи более общего характера, в которых "отыскиваются кривые, обладающие максимальным или минимальным свойством". В качестве одного из первых примеров Эйлер ищет - и находит!- кривую проходящую через две данные точки, для которой ∫xⁿds имел бы минимальное значение. Это - простейшая задача вариационного исчисления - нового для того времени раздела математики, имеющего ныне весьма широкое применение.

В дальнейшем Эйлер использует полученные результаты в механике. Тело, не находящееся под действием каких-либо сил, доказывает он, движется на данной поверхности именно по геодезическим линиям.

Наконец, в 1744 г. Эйлер публикует "Решение изопериметрической задачи в самом широком смысле". Это было первым в мире серьезным сочинением по вариационному исчислению.

Во второй период жизни в Петербурге Эйлер вновь возвращается к проблеме. В 1767 г. он пишет работу "Исследования по кривизне поверхностей", в которой доказывает важную теорему о кривизне нормального сечения поверхности. Немного позднее (1770-1771) он занялся исследованием развертывающихся поверхностей и установил зависимости между координатами х, у точек поверхности и соответствующими координатами и, v точек развертки (рис. 9) этой поверхности на плоскость. Это оказалось особенно важным для составления карт - области, в которой Эйлер и до этого работал весьма успешно.

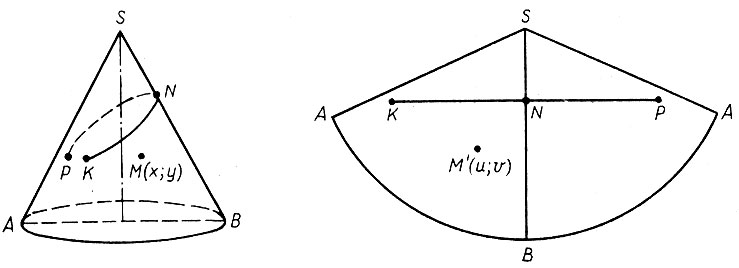
Рис. 9