7. Дифференциальные уравнения

В XVII в. французский математик и философ Рене Декарт ввел в рассмотрение переменные величины. "Благодаря этому в математику вошли движение и диалектика и благодаря этому же стало немедленно необходимым дифференциальное и интегральное исчисление",- пишет Энгельс в "Диалектике природы". С этого времени математика рассматривает не только числа, величины и фигуры, но также и процессы, изменения величин во времени. В XVIII в. стало необходимым изучение зависимостей между переменными величинами. Наряду с уравнениями, в которых неизвестными служат числа, появились уравнения, в которых неизвестны и подлежат определению функции.

К XVIII в. на первый план в математике и ее приложениях выдвинулось понятие функции.

Изучение переменных величин и функциональной зависимости сразу же потребовало развития математического анализа, основы которого были заложены Ньютоном и Лейбницем.

Во многих задачах быстро развивающегося естествознания неизвестные функции оказались связанными со скоростью их изменения - иначе говоря, устанавливалась взаимосвязь между функцией и ее производной; позднее в рассмотрение вошли производные от производных или, иначе, производные высших порядков. По этой зависимости, которую записывали в форме уравнения, и требовалось обычно отыскать неизвестную функцию. Подобные уравнения называются в математическом анализе дифференциальными уравнениями.

Некоторые простейшие дифференциальные уравнения решаются путем интегрирования, т. е. квадратурой; более сложные дифференциальные уравнения долгое время вообще не умели решать. Поэтому нахождение способа решения каждого нового типа дифференциальных уравнений было важным открытием, способствовавшим развитию математики и ее приложений в естественных и технических науках.

Приведем пример. По закону Ньютона скорость охлаждения нагретого тела пропорциональна разности температур тела и окружающей среды. Пусть металлическая болванка, имеющая начальную температуру Т₀ = 300°С, брошена в воду, имеющую температуру Т_ср = 60°С (воды много, ее температура при охлаждении болванки практически не изменяется). Требуется найти функцию, выражающую зависимость температуры болванки Т от времени t и определить t, для которого будет T_t =150⁰С. если через t₁ = 10 мин температура болванки станет T₁₀ = 200°С.

Обозначим переменную температуру болванки через х. Тогда разность температур тела и жидкости в каждый момент времени t равна (х-60) °С; изменение температуры за малое время Δt составляет Δх; предполагается, что за очень малое время Δt изменение температуры незначительно и скорость этого изменения сохраняет "постоянное" значение .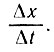

Если "коэффициент пропорциональности" в законе Ньютона обозначить через K, то можно записать равенство

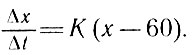
Однако это равенство - приближенное, ибо скорость изменения температуры лишь "почти" сохраняет постоянное значение. Чтобы равенство стало точным, необходимо в левой части заменить приращения дифференциалами (перейти к пределу при условии Δt → 0). Тогда

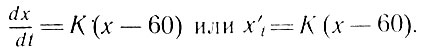
Это - простейшее дифференциальное уравнение; ему удовлетворяет функция

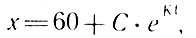
где С - произвольная постоянная величина.

Чтобы определить С, используем "начальное условие": в начальный момент времени, т. е. при t₀ = 0, было T₀ = 300, поэтому

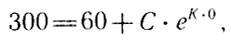
откуда С = 240, а потому

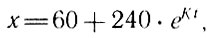
Чтобы определить К, воспользуемся дополнительным условием T₁₀ = 200:

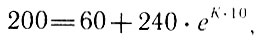
откуда с помощью, скажем, таблиц логарифмов находим

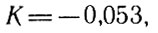
и температура болванки х (градусов Цельсия) характеризуется искомой функцией времени t (мин):

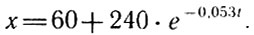
Чтобы ответить на вопрос задачи, остается лишь подставить в эту функцию х = 150°:

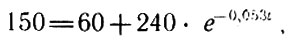
откуда непосредственным вычислением получаем

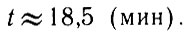
Уже в первый период своей работы в Петербурге Эйлер нашел решение нескольких типов дифференциальных уравнений, а в 1739 г. впервые показал общий метод решения линейных дифференциальных уравнений любого порядка (т. е. таких, в которые входят неизвестная функция, ее производная, производная от производной и т. д. любого порядка) - но только с постоянными коэффициентами. А именно такие уравнения чаще всего и встречаются в механике. Например, линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид

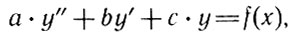
где а, b, с - постоянные величины. Немного позднее Эйлер нашел решение более сложного типа уравнений

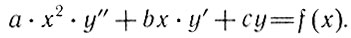
Уравнения этого типа, также часто встречающиеся в приложениях, и поныне называются "уравнениями Эйлера".

Если искомая функция зависит от двух, трех, вообще - от нескольких переменных, то приходится рассматривать системы дифференциальных уравнений с частными производными, играющие особенно важную роль в физике. Рассказ о них в популярной книге оказался бы чересчур сложным; скажем лишь, что Эйлер заложил основы общей теории подобных систем уравнений первого и второго порядков, а французские математики Д'Аламбер, Лагранж, Монж и Лаплас позднее развили и расширили теорию дифференциальных уравнений с частными производными. Особенно важные результаты в исследовании дифференциальных уравнений принадлежат крупнейшему французскому математику Анри Пуанкаре (1854-1912).