6. Математический анализ и специальные функции

Еще Иоганн Бернулли определил функцию как "количество, составленное любым способом из переменной величины и постоянных".

В начале первого тома "Введения в анализ бесконечных", вышедшего в 1748 г. в Лозанне (Швейцария), Эйлер уточняет определение своего учителя:

"Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного и чисел или постоянных количеств". Далее Эйлер различает функции явные и неявные. Скажем, функции 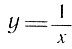- явная, а уравнение х²+у² = а² выражает неявную функцию, которая может быть определена (хотя и не во всех случаях) путем решения уравнения относительно у. Там же формулируется предложение о существовании обратной функции и функции, заданной параметрически.

Если задана функция y = 3х+8, то, решая уравнение относительно х, получим 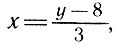а потому функция 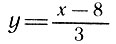является обратной по отношению к данной функции. Если дана функция y = sin х, то обратной будет функция x = arcsin y.

Совокупность равенств 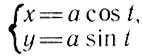выражает ту же функцию, что и х²+у² = а², в чем можно убедиться, если возвести оба данных равенства в квадрат и сложить почленно:

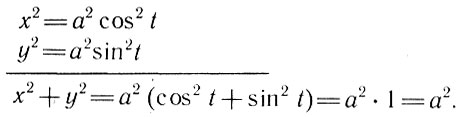
Здесь параметр t, через который первоначально выражены х и у, можно рассматривать как угол, составленный вектором 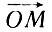и осью абсцисс (рис. 6). При изменении этого угла от 0 до 2π точка М(х, у) будет описывать окружность радиуса r = а.

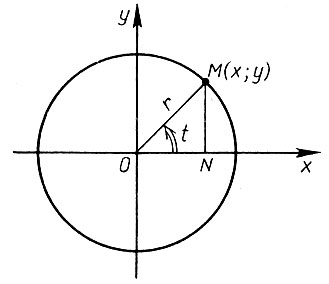
Рис. 6

В предисловии к "Наставлению по дифференциальному исчислению" (1755) Эйлер дает новое определение функции:

"Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых". При всей витиеватости выражений XVIII в. это определение ничем, по существу, не отличается от классических определений, сформулированных в XIX в. Лобачевским и Лежен-Дирихле.

Эйлер рассмотрел разделение функции на однозначные и многозначные, выделил классы четных и нечетных функций. Вся его классификация вошла в употребление в математике и сохраняется по сей день.

Вместе с тем, Эйлер понимал, что существуют и "неаналитические" функции. Уже в статье "О колебаниях струны", написанной в 1748 г. и опубликованной в Берлине в 1850 г., он указывает, что кривая, рассматриваемая как изображение функции, может оказаться и более сложной, чем объединение нескольких (вообще - конечного числа)"дуг непрерывных линий. Таковыми, в частности, являются функции, получающиеся при интегрировании дифференциальных уравнений.

"В анализе появляются также разрывные функции, что многим видным математикам представляется противоречивым,- писал он позднее в III томе своего "Интегрального исчисления" (1770).- Особенная сила интеграции, рассматриваемых в этой книге, в том и состоит, что при них могут встречаться и разрывные функции; благодаря этому новому (т. е. интегральному.- А. Я) исчислению границы анализа значительно расширяются".

"Что такое дифференциальное исчисление?"- риторически вопрошает Эйлер и определяет его как "метод определения отношения исчезающих приращений, получаемых какими-либо функциями, когда переменному количеству, функциями которого они являются, дается исчезающее (то есть исчезающе малое, по современной терминологии бесконечно малое.- А. Я.) приращение".

Итак, по Эйлеру, истинным объектом дифференциального исчисления является производная, то есть отношение исчезающе малого приращения функции к исчезающе малому приращению аргумента или, пользуясь современными обозначениями:

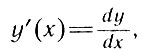
что следует понимать как

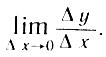
Бесконечно малые величины Эйлер во многих рассуждениях полагает равными нулю - и все же получает верные выводы. В то же время он правильно считает, что отношение двух таких "нулей", то есть отношение бесконечно малого приращения функции к соответствующему приращению аргумента, перестает быть неопределенным - поэтому их следует обозначать различными символами, например dx, dy и т. д., ибо они могут иметь различные отношения.

Эйлер еще не считает нужным обосновывать каждое утверждение, не обсуждает и тем более не обосновывает теорию пределов, но в то же время различает порядки бесконечно малых. Этот стиль - практическая применимость и безошибочность при отсутствии строгих доказательств - вообще характерен для математики XVIII столетия. Этот стиль "правдоподобных рассуждений" - наилучший при знакомстве с существом тех или иных явлений и закономерностей, когда требуется разобраться в фактах, но еще не наступило время для строгого обоснования и дедуктивного построения теории. Именно так следует впервые знакомиться с отдельными разделами физико-математических наук; лишь когда существо явления станет понятным, можно будет говорить о его первопричинах и строгих обоснованиях,- но это нужно, разумеется, лишь тем немногим, кто посвятит свою жизнь глубокому изучению точных наук.

Именно таким путем шло развитие точных наук в XVIII и первой половине XIX в. Понятия математики и не всегда строго обоснованные формулы применялись - и в подавляющем большинстве случаев приводили к верным результатам. А обоснования фундаментальных начал анализа появились лишь в работах выдающихся математиков XIX в. К. Вейерштрасса и О. Коши.

Однако Эйлер занимался в анализе не только рассуждениями и исследованиями. Он разработал и конкретные приемы интегрирования многих функций, которые и по сей день изучаются студентами вузов. Мы рассмотрим здесь три примера.

Напомним, что для нахождения производных предусмотрены правила, применимые к любой элементарной функции. Обратное же действие, нахождение первообразной функции, или неопределенного интеграла, значительно сложнее и, как указывал Эйлер, может привести к функциям нового типа.

Весьма важным классом функций, интегрирование которых всегда может быть выполнено в конечном виде^*, являются дробно-рациональные функции, представляющие собой частное двух многочленов. Мы будем предполагать, что умеем разложить югочлен в знаменателе на множители первой и второй степени^**. Эйлер предложил разложение дробей на простейшие, то есть на кие, знаменатели которых - линейные двучлены либо не разлагающиеся на линейные множители квадратные трехчлены.

^* (Практическое выполнение может оказаться громоздким. В последние годы эмоздкие интегрирования предпочитают выполнять приближенно с помощью ЭВМ.)

^** (Для этого необходимо найти корни многочлена, записанного в знаменателе. Это всегда можно выполнить с достаточной точностью.)

1°. Рассмотрим

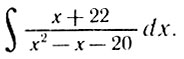
Очевидно, дробь

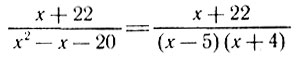
"произошла" от приведения к общему знаменателю дробей вида

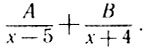
Каждую из таких дробей интегрировать очень легко, например:

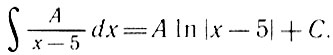
Эйлер и предложил разлагать дроби с составным знаменателем на простейшие. Чтобы определить А и В, можно, скажем, воспользоваться методом неопределенных коэффициентов:

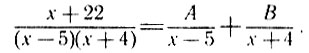
Приводя обе части равенства к общему знаменателю и отбрасывая его, получим

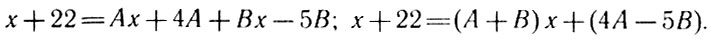
Так как это равенство выполняется тождественно, то есть при любых числовых значениях переменной х, то коэффициенты при одинаковых степенях х должны быть равны:

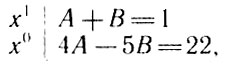
откуда находим А = 3, В = -2, или

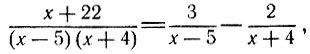
и, окончательно,

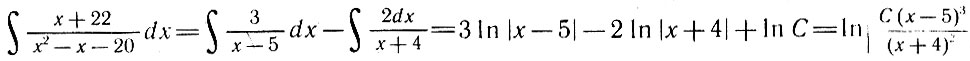
2°. Эйлер предложил также некоторые подстановки, сводящие интеграл, содержащий 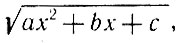, к интегралу от рациональных функций, который, как мы упоминали выше, всегда может быть вычислен в конечном виде.

Студентам и поныне часто предлагают примеры вида:

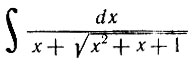
Положим 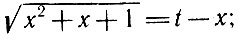тогда

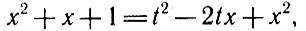
откуда

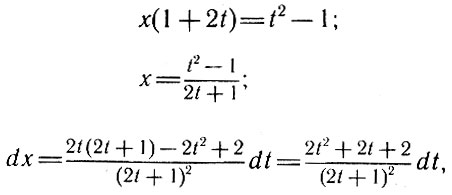
и мы получаем интеграл от рациональной функции

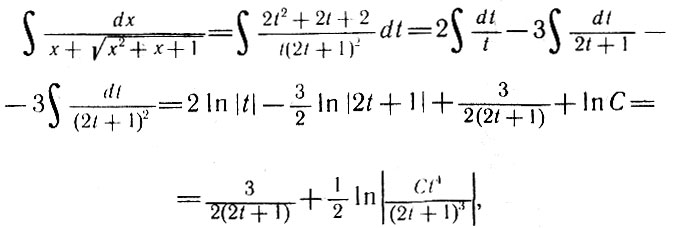
где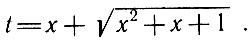

3°. Интегралы вида 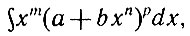где m, n, p - любые рациональные числа, носят название интегралов от биномиальных дифференциалов. Эти интегралы могут быть вычислены в конечном виде при выполнении хотя бы одного из трех условий:

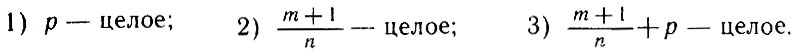
Эти три случая были, впрочем, известны еще Ньютону. Эйлер указал для каждого из этих случаев подстановки, позволяющие непосредственно вычислить первообразную в конечном виде. А в следующем столетии русский математик П. Л. Чебышев строго доказал, что если ни одно из этих трех условий не выполняется, то первообразную нельзя выразить в конечном виде.

Д. Бернулли в одном из писем к X. Гольдбаху впервые вводит число е (не пользуясь этим символом) как 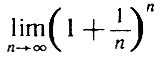- и сразу же записывает это число в форме бесконечного ряда

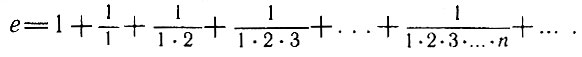
Эйлер обобщил рассуждение Бернулли, показав, что

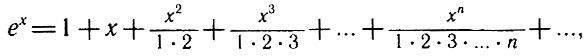
и, как бы между прочим, вычислил значение е с 24 верными знаками.

Чуть позднее Эйлер по-новому вывел разложения в ряд для синуса и косинуса, известные ныне каждому студенту и включенные даже в таблицы В. М. Брадиса для средней школы:

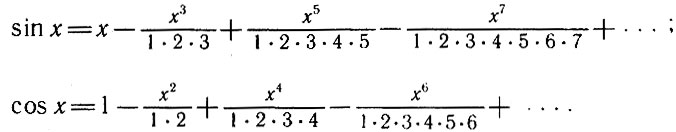
"Отрицательные числа логарифмов не имеют",- убеждены многие школьники. Однако это утверждение не совсем верно.

Второклассник, скажем, считает, что 7 на 5 "не делится": он еще не знает о существовании дробей и не ведает, что 7:5 = ⁷/₅ или 7:5 = 1,4. Третьеклассник, даже отличник, уверен в том, что из 3 нельзя вычесть 5. Старшеклассники часто считают, что корень квадратный, скажем, из трех "не извлекается"; однако существует ведь "точное" иррациональное число 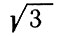; его можно выразить приближенно десятичной дробью с любой требуемой точностью. В этом же смысле "существуют" и логарифмы отрицательных чисел; однако эти логарифмы являются числами новой природы - мнимыми числами^*, представителем которых является "мнимая единица", обозначаемая через i и определяемая так:

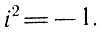
^* (Вот уже несколько лет, как изучение мнимых чисел в нашей средней школе не является обязательным.)

Еще в 1717 г. английский математик Р. Коутс высказал (в геометрической форме) предложение о связи между показательной и тригонометрическими функциями от мнимого аргумента. Позднее Эйлер заметил, что разложения в ряд показательных и тригонометрических функций "почти совпадают" - и вывел знаменитые формулы Эйлера, которые в современной символике (обозначая мнимую единицу через i) можно записать

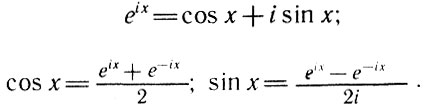
Полагая в первой из этих формул х = π, получим

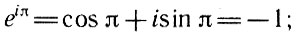
поэтому удобно считать, что. натуральный логарифм числа -1 равен iπ:

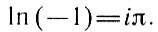
Приведенные выше формулы играют ныне основополагающую роль в важной области математики - теории функций комплексного переменного, широко применяемой в электро- и радиотехнике и во многих других отраслях современной техники.

Отметим кстати, что Эйлер ввел во всеобщее употребление обозначение л для отношения длины окружности к ее диаметру и обозначение е для основания натуральных логарифмов. Синус и косинус тоже лишь со времен Эйлера стали рассматриваться как функции; до него синус и косинус считались лишь определенными отрезками в круге или длинами этих отрезков, выражаемыми в долях радиуса.

Эйлер сформулировал и доказал ряд важных тождеств, известных ныне каждому школьнику под названием "формул приведения".

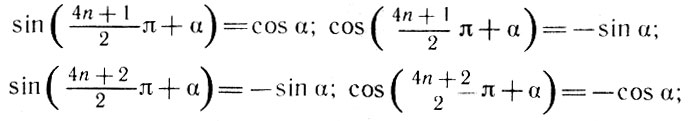
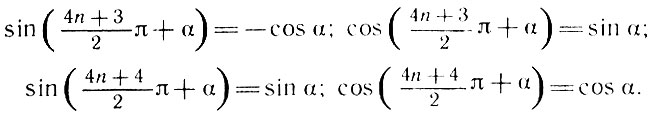
Уже в первые годы пребывания в Петербурге Эйлер пытался найти формулу для общего выражения суммы так называемого гипергеометрического ряда

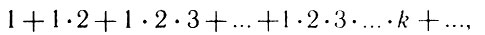
и в 1728 г. сделал на заседании Академии доклад "Об общих членах рядов". К сожалению, рассуждения Эйлера содержат довольно громоздкие действия с интегралами; поэтому отметим лишь, что в итоге Эйлер пришел к выражению через интегралы двух важнейших функций, которые и были названы эйлеровыми интегралами первого и второго рода, а позднее - бета-функцией Эйлера и гамма-функцией Эйлера.

Во второй период пребывания в Петербурге Эйлер уже систематически разработал теорию таких функций, определил соотношение между бета- и гамма-функцией и нашел связь этих функций с эллиптическими интегралами.

Рассматривая некоторые вопросы колебания мембран в своих работах по акустике, Эйлер столкнулся с другим видом специальных функций - цилиндрическими функциями первого и второго рода. Позднее, во II томе "Интегрального исчисления" Эйлер нашел выражение и для этих функций через степенные ряды.

Дальнейшие результаты в теории гамма-функции были получены полвека спустя Н. И. Лобачевским, а еще позднее - советским математиком В. А. Стекловым.