
5. Теория вероятностей
Многим знакома игра "Спортлото". Уплатив 30 копеек, каждый желающий отмечает на карточке несколько чисел. Возможность выиграть в лотерее нетрудно оценить заранее, пользуясь несложными правилами комбинаторики и теории вероятностей.
В некоторых странах уже более двухсот лет назад начали проводить так называемую "генуэзскую лотерею". Желающие участвовать покупали билеты с числами от 1 до 90 и отмечали одно, два, три, четыре или пять из этих чисел. В день розыгрыша из мешка, содержавшего номера от 1 до 90, вытаскивали случайным образом 5 номеров; выигрывали те и только те билеты, все номера которых оказывались среди вытянутых.
Владелец выигравшего билета с одним отмеченным номером получал в 15 раз больше стоимости билета; с двумя номерами - в 270 раз; с тремя - в 5500 раз; с четырьмя - в 75 000 раз и с пятью выигравшими номерами - в миллион раз больше стоимости билета. Если же на билете был отмечен хоть один из невытянутых в лотерее номеров - билет не выигрывал.
В начале XVIII в. лотерейная горячка охватила Италию. Многие тратили на лотерейные билеты последние гроши, надеясь ухватить "счастье" - угадать пять, четыре или хотя бы три числа и обогатиться. Однако вероятность угадать все пять чисел из 90 составляет
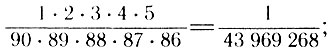
иначе говоря, такой выигрыш возможен в среднем один раз из почти 44 миллионов попыток.
В 1749 г. итальянец Рокколини предложил Фридриху II организовать генуэзскую лотерею. 15 сентября того же года Фридрих направил письмо Эйлеру - просил консультацию по этому поводу. Аналогичное письмо Эйлер получил несколько лет спустя, когда Фридриху предложили провести лотерею "для помощи населению, пострадавшему от бедствий семилетней войны".
Эйлер решил задачу и представил в Берлинскую Академию сочинение "Решение одного очень трудного вопроса теории вероятностей" - экспертизу относительно предлагаемых лотерей. Позднее это сочинение было опубликовано в изданиях Берлинской Академии.
Эйлер рассчитал не только вероятность выигрышей, но и вероятности секвенций, то есть появления в данном тираже двух или нескольких последовательных чисел. Например, выпадение номеров 17, 18, 19, 20, 21 дает секвенцию пяти чисел; выпадение 12, 17, 18, 19, 58 дает секвенцию трех чисел и отдельно два изолированных числа или 1(3)+2(1); выпадение 17, 18, 19, 58, 59 дает 1(3)+1(2) и т.п. Ученый вывел общие формулы, рассмотрел вероятности и количество вариантов для всех семи случаев, встречающихся при вытягивании пяти номеров из 90.

Седьмой случай, наиболее вероятный, как рассчитал Эйлер, когда секвенции не появляются.
Различные исследования Эйлера по теории вероятностей в основном были связаны с азартными играми и лотереями и лишь частично - с проблемами демографии и страхового дела. За пределы этих проблем не выходили запросы науки и техники того времени.
XVIII в. прошел под знаком повышенного интереса к демографии. Люди стали интересоваться вопросами рождаемости, смертности, средней продолжительности жизни, ростом народонаселения и, в частности, исчислением срока удвоения населения. Не мог пройти мимо этих вопросов и Эйлер. Так, в его "Введении в анализ" (1748) сформулированы и разобраны следующие задачи:
1. Число жителей некоторой области увеличивается ежегодно на 1/30 свою часть вначале в области было 100 000 жителей; каково будет число жителей области через 100 лет?
2. После библейского потопа род человеческий размножился, якобы, от 6 человек; допустим, что через 200 лет стало 1 000 000 людей; на какую свою часть число людей должно было возрастать ежегодно?
3. Предположим, что к концу каждого века население удваивается; найти годовой прирост.
Вычисления Эйлера дали на эти задачи следующие ответы: 1) 2654 874; 2) на 1/16 часть (примечание Эйлера: если бы и далее рост числа людей шел в таком же соотношении, то в последующие 200 лет их стало бы 166 666 666 666, и для их прокормления не хватило бы всей Земли); 3) на 1/144 часть.
Весьма интересно следующее рассуждение Эйлера.
Пусть в каком-то году родилось N людей.
Через год останется в живых N1 людей,
через два года останется в живых N2 людей,
......................................................
через k лет останется в живых Nk людей.
Значит: в возрасте до 1 года, то есть на I году жизни умрет N-N1.
на II году умрет N1-N2;
на III году умрет N2-N3;
..............................................
на k-м году умрет Nk-1-Nk людей и т. д.
Эта идея Эйлера о выживании и вымирании служит основой для демографических расчетов и по сей день.
Эйлер сформулировал 6 важных задач демографии и указал формулы для их решения, например:
1. Найти вероятность того, что лицо возраста т лет проживет еще n лет (ответ: 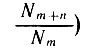 ); вероятность умереть в течение того же срока для этого лица составит
); вероятность умереть в течение того же срока для этого лица составит 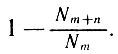
2. Для лица в возрасте m лет найти вероятность смерти через n лет, то есть в промежуток от n до (n+1) лет, начиная с данного момента. (Ответ. 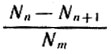 )
)
3. Из данной группы в М лиц данного возраста m лет найти число лиц, которые проживут еще n лет (ответ: 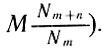 )
)
4. Для человека в возрасте m лет найти число z лет, которые он еще проживет с вероятностью 0,5. Искомое число лет находится из равенства 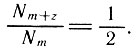
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'