4. Теория чисел

Эйлер написал более ста сочинений по теории чисел.

Еще в XVII в. юрист из Тулузы Пьер Ферма, ставший одним из крупнейших математиков Франции, высказал - большей частью без доказательств - много интересных предложений, относящихся к целым числам. Однако Ферма, как правило, высказывал свои предложения лишь в предположительной форме, подкрепляя их примерами, но без строгих доказательств. А Эйлер подробно исследовал эти предложения и либо доказывал их, либо опровергал. Мы рассмотрим здесь некоторые примеры.

Если р - простое число и а не делится на р, то n = (а^р-1 - 1) всегда делится на р. Эта теорема носит название "малой теоремы Ферма"; она имеет очень большое значение для теории сравнений.

Два натуральных числа а и b, дающие при делении на натуральное число m один и тот же остаток r, называются равноостаточными или сравнимыми по модулю m. Записывают это так:

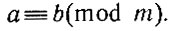
Например, 53 и 38 при делении на 5 дают один и тот же остаток 3. Поэтому они сравнимы по модулю 5:

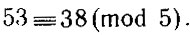
В частности, если некоторое число n делится на m, то говорят, что оно сравнимо с нулем по модулю m. Например:

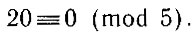
По признаку делимости на 5 все натуральные числа можно разбить на 5 классов:

класс С₀, содержащий 5, 10, 15, ..., вообще все числа вида 5k;

класс С₁, -//- 1, 6, 11, ..., вообще все числа вида 5k+1;

класс С₂, -//- 2, 7, 12, ..., -//-//- 5k+2;

класс С₃, -//- 3, 8, 13, ..., -//-//- 5k+3;

класс С₄, -//- 4, 9, 14, ..., -//-//- 5k+4.

Эти классы называют классами вычетов по модулю 5. Разумеется, при разбиении по модулю m мы получили бы ровно m классов.

Если для каждого из классов выбрать по одному представителю - скажем, числа 15, 21, 12, 3 и 49, то мы получим полную систему вычетов по модулю 5. Чаще всего в качестве представителей выбирают попросту остатки от деления на модуль; в данном случае получится система 0, 1,2, 3, 4.

Эйлер продолжал работы Ферма в области теории чисел. Он, в частности, ввел функцию φ (m), которая называется функцией Эйлера - количество натуральных чисел, меньше данного m и взаимно простых с ним. Так, φ (6) = 2, потому что только два числа, 1 и 5, меньших шести, взаимно просты (не имеют общих делителей) с числом 6; φ (10) = 4, потому что только числа 1, 3, 7, 9 взаимно просты с числом 10. Если р - простое число, то все меньшие числа взаимно просты с р и φ (р)= р - 1.

Эйлер обобщил малую теорему Ферма и доказал, что если а и m взаимно простые числа - это можно записать (а, m)= 1,- то (а^{φ (m)}-1) делится на m. Это предложение называется теоремой Эйлера (о сравнениях). Добавим еще, что Эйлер разработал основы теории степенных вычетов.

Любителям математики знакома "великая теорема Ферма": требуется найти целые числа х, у, z так, чтобы для какого-нибудь целого n ≥ 3 выполнялось равенство xⁿ+yⁿ = zⁿ, или доказать, что такое равенство невозможно. Эйлер доказал невозможность равенства для n = 3 и для n = 4. Позднее невозможность равенства была доказана для некоторых других значений n; однако полного, общего доказательства до сего времени найти не удалось.

Отметим кстати, что для суммы не двух, а большего числа слагаемых подобное равенство возможно, например

В 1940 г. было высказано предположение, что равенство

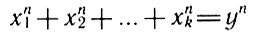
возможно в том и только в том случае, когда k ≥ n. Если бы это предположение удалось доказать, то из него как частный случай вытекало бы и доказательство "великой теоремы Ферма".

Ряд простых чисел 2, 3, 5, 7, 11, 13, 17, ... - бесконечен. Этот факт доказал еще Евклид. Если, напротив, допустить, что существует только n простых чисел x₁, x₂, ..., x_n, то число

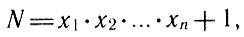
которое больше любого из этих чисел, не делится ни на одно из них. Значит, либо оно само - простое, либо делится на какие-то другие числа - и, следовательно, существует еще хоть одно простое число, что противоречит допущению о конечности ряда простых чисел. Эйлер дал новое аналитическое доказательство бесконечности ряда простых чисел; тем самым было заложено начало аналитической теории чисел.

Немало проблем теории чисел обсуждалось Эйлером в его переписке с Христианом Гольдбахом. Изучение этой переписки подтверждает несомненное математическое дарование Гольдбаха, хотя оно не может идти в сравнение с гениальностью Эйлера (отметим, кстати, что позднее Гольдбах сделал блестящую карьеру на дипломатической службе, но долгие годы продолжал научную переписку с Эйлером). Из их переписки возникла, например, знаменитая "Проблема Гольдбаха", состоявшая из двух гипотез:

1) всякое нечетное число, большее шести, есть сумма трех простых чисел;

2) всякое четное число есть сумма двух простых чисел.

Рассмотрение этих проблем^* и другие работы Эйлера составили основы аддитивной теории чисел - теории разложения данного целого числа на слагаемые определенного вида.

^* (B общем виде эти проблемы не решены и поныне. В 1937 г. академик И. М. Виноградов с помощью разработанного им метода оценок тригонометрических сумм доказал, что каждое достаточно большое нечетное число действительно является суммой трех простых. Значит, достаточно большое четное - сумма четырех простых.)

Следует упомянуть еще о работах Эйлера по исследованию чисел вида 4k+1 и представлению их в виде суммы двух квадратов; о работах по теории цепных дробей (см. предыдущий раздел); наконец, в 1772 г. Эйлер эмпирически нашел так называемый закон взаимности, оказавшийся полезным для решения неопределенных уравнений второй степени.