3. Непрерывные дроби

Рассмотрим последовательность

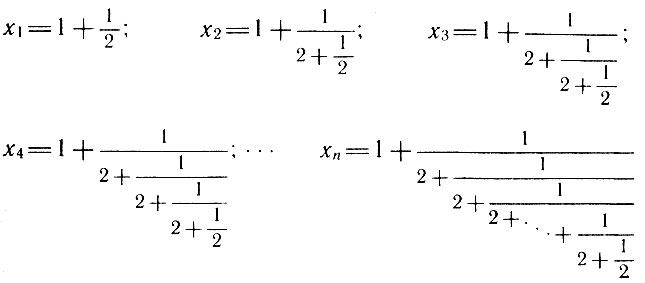
Нетрудно подсчитать, что

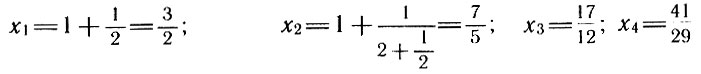
А что будет получаться при дальнейшем возрастании n? Существует ли предел 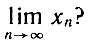Чему может равняться этот предел?

Рассмотрим положительное число х, определяемое как предел выражения

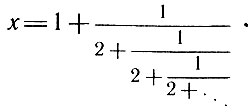
Перенесем единицу влево:

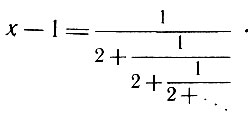
Это равенство равносильно такому:

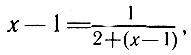
откуда (х-1 (2+x-1) = 1 и, следовательно, 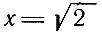или

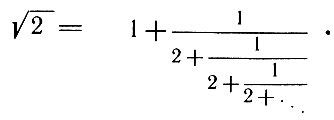
Выражение в правой части называется цепной или непрерывной дробью. В общем виде ее можно записать так:

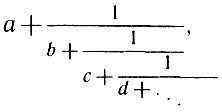
где а, b, с, d, вообще говоря, различные целые числа.

Если, начиная с некоторого места, повторяются одинаковые числа (или одинаковые конечные последовательности чисел), то непрерывная дробь называется периодической. Выше показано, что число 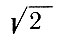может быть записано в виде периодической непрерывной дроби, хотя, как известно, это число, как и всякое другое иррациональное число, невозможно записать в виде десятичной периодической дроби.

Если десятичную периодическую дробь оборвать на каком-либо месте, мы получим ее приближенное значение (с недостатком). Например:

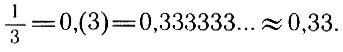
Оборвав непрерывную дробь, мы тоже получим ее приближенное значение в виде рационального числа. Мы видели, что 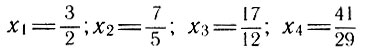и т. д. Эти дроби называют подходящими дробями для данной непрерывной дроби; в самом деле, каждая следующая подходящая дробь все ближе подходит к предельному значению данной дроби, или, иначе, дает все более точное приближение этого значения.

Можно доказать, что подходящие дроби четного порядка всегда меньше их предельного значения, а подходящие дроби нечетного порядка больше их предельного значения. Например, нетрудно проверить, что

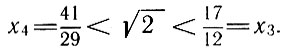
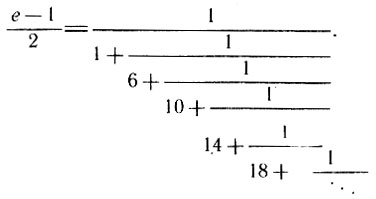
В статье "О непрерывных дробях" (1737) Эйлер впервые указал приемы преобразования таких дробей и показал связь непрерывных периодических дробей с квадратными уравнениями и квадратическими иррациональностями. Там же показано выражение основания натуральных логарифмов, числа е^* (е = 2,71828182845...), с помощью непериодической непрерывной дроби

^* (Число е можно определить как 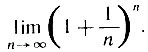. Оно играет, как и число π, важную роль в анализе и его приложениях.)

Вот еще некоторые простые разложения в непрерывные дроби, найденные Эйлером:

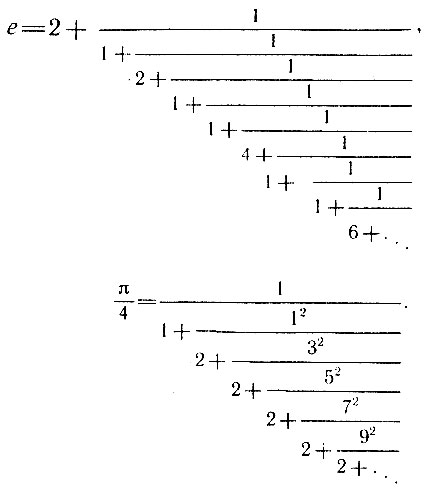
Разлагая в бесконечную цепную дробь е и е², Эйлер, по существу, доказал иррациональность этих чисел, т. е. невозможность равенств 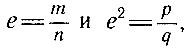, где m, n, р, q - произвольные натуральные числа.

Пользуясь этим, И. Г. Ламберт несколько лет спустя получил представление некоторых функций в форме бесконечных непрерывных дробей, например

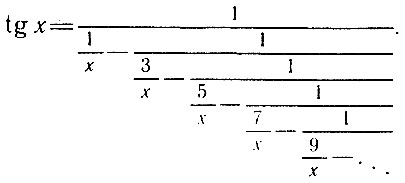
Позднее выяснилось также, что непрерывные дроби могут быть использованы для приближенного решения уравнений. А в 1759 г. Эйлер представил в Петербургскую Академию 2 статьи о применении непрерывных дробей для нахождения целых решений так называемого "уравнения Пелля", имеющего вид

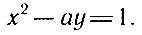
Непрерывные дроби часто используются для приближения иррациональных чисел рациональными. Так, исторически известные приближенные значения числа 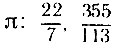и т. д.- являются, как выяснилось, значениями подходящих дробей для изображения числа я в форме непрерывной дроби. Подробные исследования непрерывных дробей выполнили впоследствии русские математики П. Л. Чебышев и А. А. Марков.