2. Теорема Эйлера о многогранниках

Многогранник - тело, ограниченное плоскими многоугольниками. Призма и пирамида - многогранники. Призма может быть треугольной (рис. 3, а) или, скажем, шестиугольной (рис. 3, б), пирамида может быть полной и иметь в основании, например, треугольник (рис. 3, в), а может быть усеченной и иметь своими основаниями, скажем, пятиугольники (рис. 3, г). Существуют 5 видов правильных многогранников, т. е. таких, все грани которых - правильные и равные между собой многоугольники (рис. 4). Многогранник называется "простым" или "односвязным", если он не имеет "дыр"; все упомянутые и изображенные выше многогранники - простые; а на рисунке 5 изображен "непростой", или "двусвязный", многогранник, имеющий сквозное отверстие.

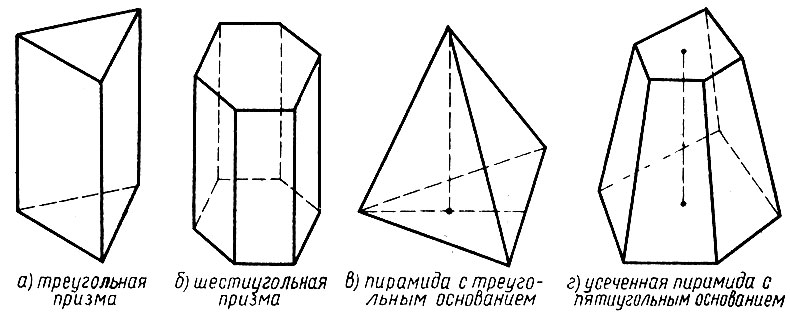
Рис. 3

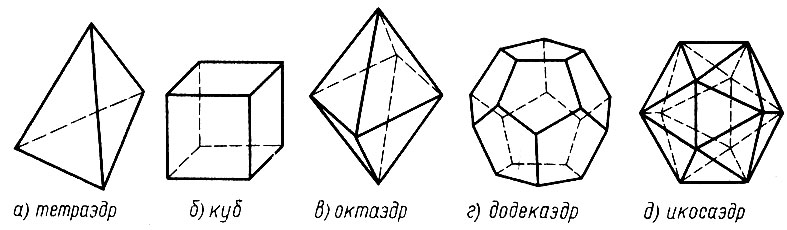
Рис. 4

Попробуем выписать число вершин (В), ребер (Р) и граней (Г) некоторых простых многогранников.

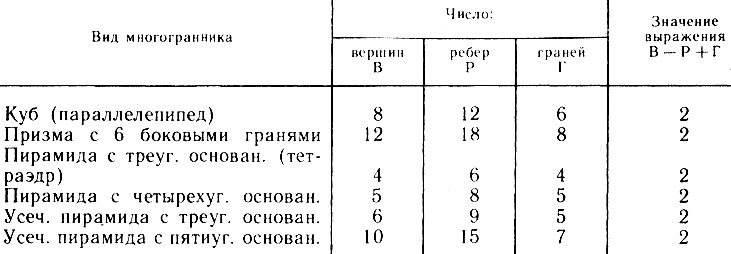
Обратите внимание на последнюю колонку таблицы: значение выражения В-Р+Г равно двум для каждого из перечисленных многогранников. Случайно ли это?

Эйлер доказал, что для любого простого многогранника

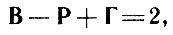
и это свойство получило название теоремы Эйлера о многогранниках.

С помощью этой теоремы, между прочим, легко доказать, что существует не более пяти видов правильных многогранников.

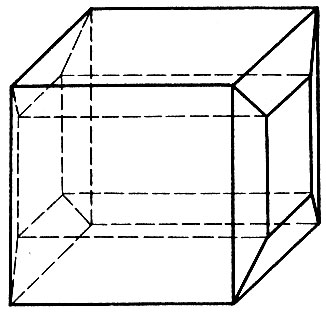
Рис. 5

В самом деле, пусть правильный многогранник имеет Г граней, каждая из которых - правильный n-угольник, а в каждой из вершин сходится по х ребер. Тогда, пересчитывая ребра, сходящиеся у каждой вершины, получим

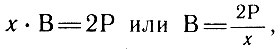
ибо каждое ребро попадает в пересчет у обоих своих концов.

Пересчитывая ребра, расположенные в каждой грани, получим

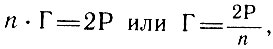
ибо здесь каждое ребро попадает в пересчет тоже по 2 раза. По теореме Эйлера 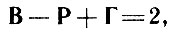то есть 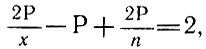или (делим все члены на 2Р)

(*)

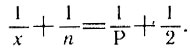Очевидно, n ≥ 3 и х ≥ 3 (многоугольник имеет не менее трех сторон, а в каждой вершине сходится не менее трех граней). Если же и n > 3, и x > 3, то

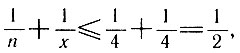
что делает равенство (*) невозможным. Отсюда следует, что либо n = 3, либо х = 3. Дальнейшие рассуждения читатель без труда проведет самостоятельно.