1. Параллелограмм и треугольник

Казалось бы, что нового можно найти в этих фигурах, которые изучались чуть ли не со времен египетских фараонов?

В феврале 1748 г. Эйлер писал Гольдбаху, что доказал теорему, которая кажется ему любопытной.

Школьникам старших классов известно, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Эйлер доказал, что в четырехугольнике, не являющемся параллелограммом, вторая сумма всегда больше первой (рис. 1).

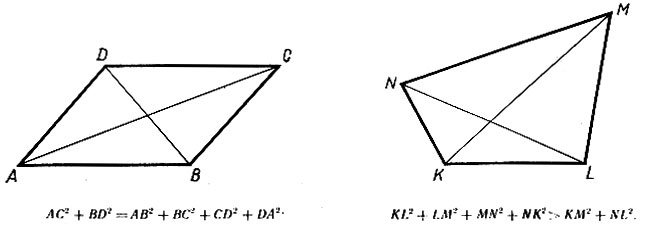
Рис. 1

Далее. Известно, что три высоты треугольника пересекаются в одной точке; эта точка Н называется ортоцентром треугольника.

Назовем середины отрезков высот треугольника от ортоцентра до каждой из вершин (т.е. точки К, Q, Р на рис. 2) точками Эйлера.

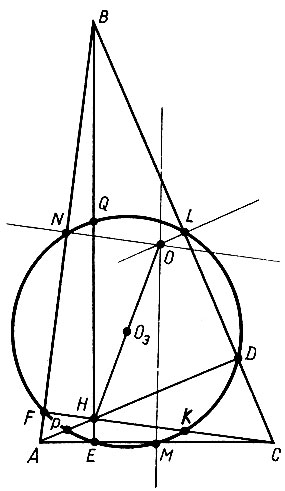
Рис. 2

В 1765 г, в "Трудах" Петербургской Академии была опубликована теорема Эйлера:Середины сторон треугольника, основания его высот и середины отрезков высот треугольника от ортоцентра до вершины лежат на одной окружности.

Эта окружность называется окружностью девяти точек или - окружностью Эйлера. Радиус ее равен половине радиуса окружности, описанной около этого треугольника.

Прямую, соединяющую ортоцентр треугольника с центром О описанной окружности, называют прямой Эйлера. Центр окружности Эйлера О_э лежит на этой прямой как раз посредине между ортоцентром и центром описанной окружности^*.

^* (С некоторыми геометрическими свойствами окружности Эйлера и прямой Эйлера можно познакомиться по книге С. И. Зетеля "Новая геометрия треугольника" (М., Учпедгиз, 1940).)