2.3. Доказательство вспомогательных утверждений

Доказательство леммы 2.2.

Обозначим 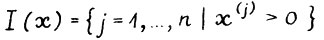, 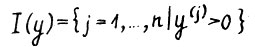. Ясно, что если 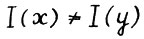,то .

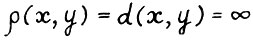Пусть 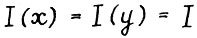. Тогда, очевидно, 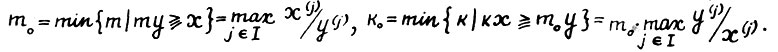. Таким образом 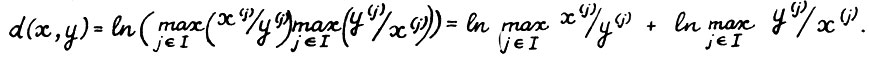(2.11)

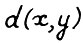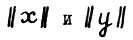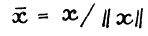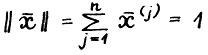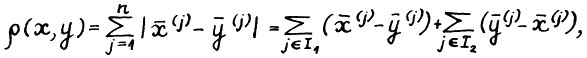Легко видеть, что не зависит от масштаба векторов x и y, т.е. от величин норм , так что метрику d можно определять на симплексе. Обозначим , тогда и , где 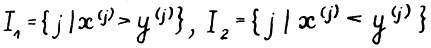следовательно,

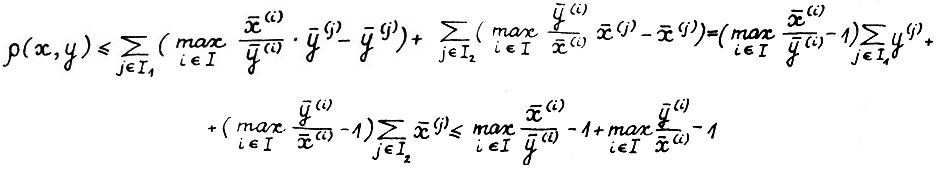
(2.12)

В силу (2.11) и независимости метрики d от масштаба, можно записать:

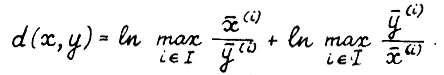
Ясно, что для 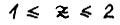справедливо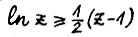 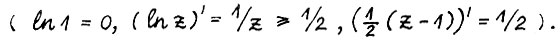Таким образом, если 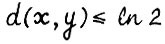, то в силу (2.12) имеем 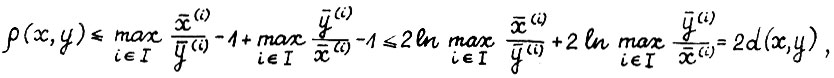что и требовалось доказать.

Доказательство леммы 2.3.

Ясно, что для любого натурального N справедливо: 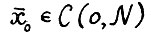, т.е. найдётся вектор 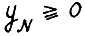, такой что 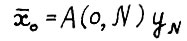. Следовательно, 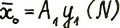, где y₁(N) = A(1, N-1)y_N и тем самым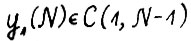

Рассмотрим последовательность 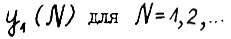и покажем, что она является ограниченной. Действительно,пусть 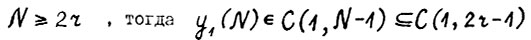и значит существует вектор y, такой что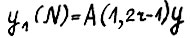

В силу А.2.1 можно записать

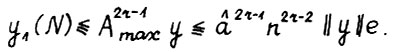
(2.13)

В то же время

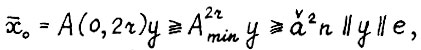
(2.14)

откуда 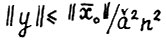, что вместе с (2.13) даёт требуемую ограниченность. Таким образом из последовательности 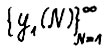можно извлечь сходящуюся подпоследовательность. Пусть 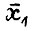- её предел, тогда 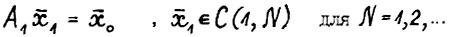, т.е. 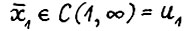. С другой стороны, точка 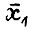определена однозначно, так как не может быть другой точки х на луче u₁, такой что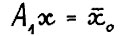

Таким же образом строятся последующие члены последовательности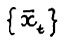

Докажем вторую часть утверждения. Положим 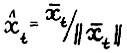. Поскольку 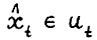, то найдётся вектор 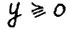, такой что 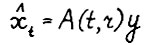. Отсюда, аналогично (2.14) имеем:

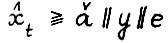
(2.15)

С другой стороны, аналогично (2.13) 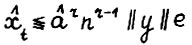, откуда 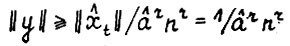, что вместе с (2.15) даёт 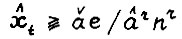, что и требовалось.

Лемма доказана.

Доказательство леммы 2.4.

Так как 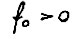и в матрице нет нулевых столбцов (иначе 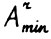не была бы положительной), то 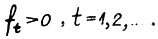. Положим 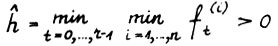. Возьмём произвольный момент t ≥ r. Поскольку 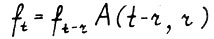, то 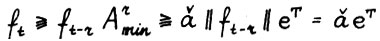. Таким образом величина 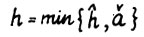является искомой. Лемма доказана.

Доказательство теоремы 2.2.

1°. Докажем сначала, что в рассматриваемой модели справеддиво утверждение леммы 1.1, т.е. для любой допустимой траектории 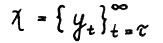существует число 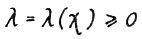, такое что 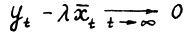. Заметим, прежде всего, что если 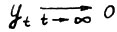, то это утверждение выполнено автоматически 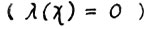, так что, не умаляя общности, можно считать, что существует последовательность моментов времени 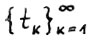и число 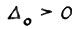, такие что 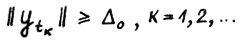. Для любого натурального 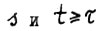можно записать 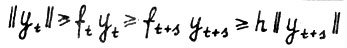, следовательно для любого t ≥ τ справедливо

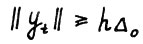
(2.16)

Вследствие (2.6) в представлениях 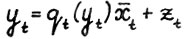, , 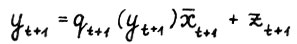векторы 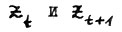неотрицательны, причём у каждого найдётся хотя бы одна нулевая координата. Поскольку 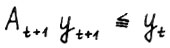, то

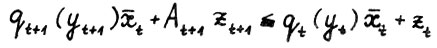
(2.17)

Отсюда, так как 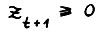, а у вектора 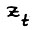, найдётся нулевая координата, имеем:

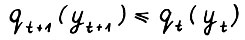
(2.18)

Поскольку величина 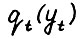ограничена снизу нулём, то существует 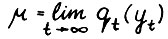. Покажем, 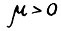. Действительно, 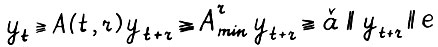, и следовательно, 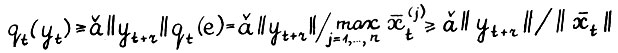. Откуда в СИЛУ (2.5) и (2.16) 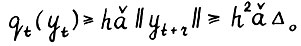, так что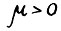

Аналогично (2.17) можно записать: 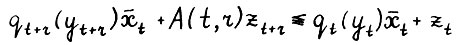, или

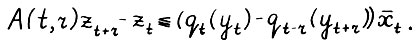
(2.19)

Пусть i - индекс, такой что 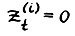, тогда отсюда и так как 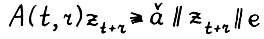, имеем: 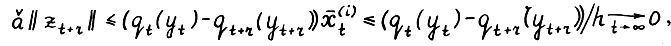, т.е. 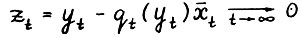, откуда

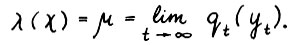
(2.20)

Для доказательства 1° осталось показать, согласно формуле (1.10), что 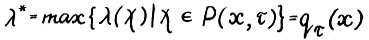для любых x > 0 и натурального τ (напомним, что Р(x,τ) обозначает множество допустимых 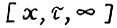- траекторий). Поcкольку 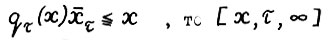- траектория вида 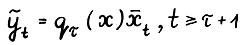является допустимой, и следовательно, 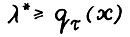. Докажем неравенство в противоположную сторону. Возьмём произвольную траекторию 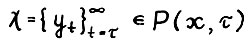. Как было доказано, 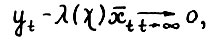, причём по (2.20) 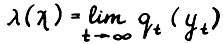, откуда в силу (2.18) 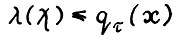. Следовательно, по произвольности выбора траектории 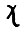имеем 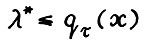, так что 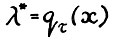и утвервдение 1° доказано.

2°. Рассмотрим вектор 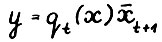. Заметим, что 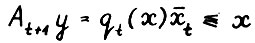, в то же время 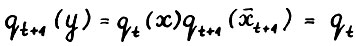. Последаее вместе с (2.18) доказывает требуемое.

3°. Пусть 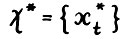- оптимальная 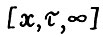- траектория. Из доказанного выше и (2.10) следует, что 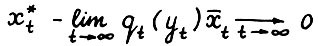. Отсюда, сравнивая 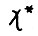с рассматривавшейся в доказательстве 1° траекторией 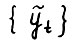, где 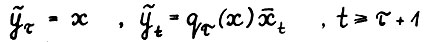, по оптимальности 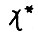и в силу (2.18) получим: 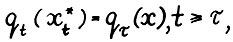, и тем самым необходимость в 3° доказана. Доказательство достаточности в теореме 1.2(3°) применимо и здесь без изменений.

Докажем вторую часть утверадения: для любой оптимальной 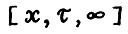- траектории 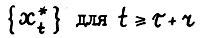выполняется 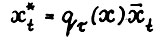. Применяя снова разложение вида 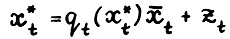, из (2.19) и так как 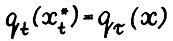, получим для любого натурального 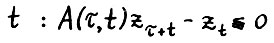. Так как при t ≥ r в матрице А(τ,r) все элементы положительны, а у вектора z_τ найдётся нулевая координата, то отсюда следует, что 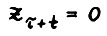, т.е. для t ≥ r справедливо 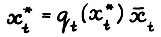, что и требовалось.

4°. Возьмём произвольное натуральное t и векторы х и y как в формулировке теоремы. Пусть для индекса i₀ выполняетс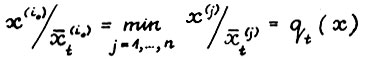я , для 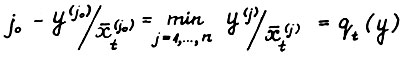. Тогда в силу (2.3), (2.5), и так как 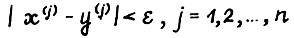, имеем:

1)

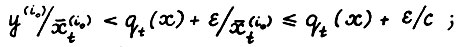
2)

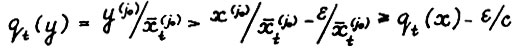
Эти два неравенства вместе дают: 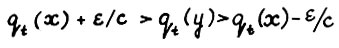, что и требовалось. Теорема доказана.

Доказательство леммы 2.5.

Предположим противное: пусть найдётся момент 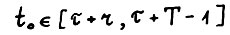, в который выполняется 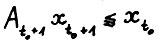, причём хотя бы для одной координаты имеет место строгое неравенство. Тогда, поскольку все элементы матрицы 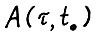положительны, справедливо 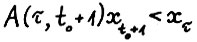и тем самым 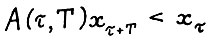. Ясно, что найдётся λ > 0, такое что верно и 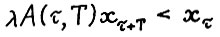, т.е. 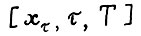- траектория вида 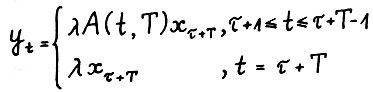является допустимой, что противоречит оптимальности 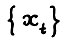. Лемма доказана.