§ 3. О сходимости скользящих планов в динамической межотраслевой модели

Рассмотрим частный случай изучавшейся в § 2 модели 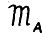, когда технологические коэффициенты неизменны во времени, т.е. А_t = A для всех t = 1,2,... , причём матрица А примитивна. Пусть α - величина, обратная к максимальному по модулю собственному значению матрицы А, 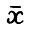и p - соответствующие нормированные правый и левый собственные векторы. По теореме Фробениуса-Перрона (см. /3, гл. XIII/) 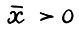, p > 0. Легко видеть, что в рассматриваемой модели тройка 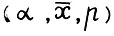является неймановским состоянием равновесия(см. /10/), где α - неймановский темп роста, 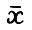- вектор выпуска, з - вектор цен.

Из теоремы 2.1, очевидно, следует, что для любого наперёд заданного ε > 0 всякий скользящий план с достаточно длинным горизонтом и начальным состоянием х(0) > 0 полностью лежит, начиная с некоторого момента, в конической кt+T ? кT,ε - окрестности неймановского луча, т.е. луча, порождаемого вектором 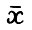. В то же время в /1/ приведён пример, показывающий, что, вообще говоря, скользящий план может не сходиться к этому лучу. А именно, пусть на каздом шаге τ + 1 процесса скользящего планирования (см. определение 4) выбирается оптимальная траектория, являющаяся решением задачи 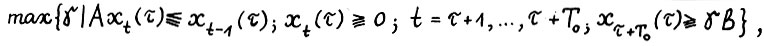, где вектор 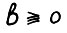задаёт требуемую структуру выпуска в конце планового периода. 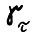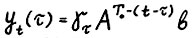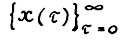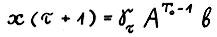Пусть - максимальное значение целевой функции в этой задаче, тогда ясно, что траектория оптимальна, и следовательно, траектория , где , является скользящим планом. Однако векторы х(τ) во зсе моменты времени τ лежат на луче 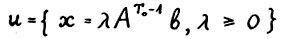, не совпадающем с неймановским лучом, и значит 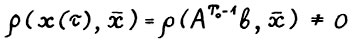для всех τ = 1,2,.... Заметим, что приведённый пример согласуется с теоремой 2.1, так как луч u лежит тем ближе к неймановскому, чем больше горизонт T₀.

В этом параграфе сходимость (в смысле пропорций) скользящих планов к неймановскому лучу доказывается при условии, что оптимизация на каждом шаге скользящего планирования состоит в максимизации выпуска в конечный момент при фиксированных пропорциях продуктов, соответствующих исходному состоянию^*. Точнее, на τ + 1 -м шаге скользящего планирования решается задача

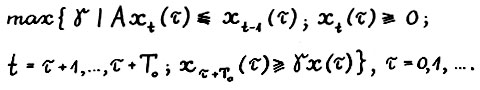
(3.1)

^* (Качественно аналогичный результат для односекторной модели получен в /24/ (подробнее см. введение).)

Теорема 3.1. Пусть 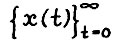- произвольный скользящий план, построенный согласно (3.1), с начальным состоянием 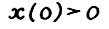. Если плановый горизонт T₀ достаточно велик (не меньше некоторого Т^*), то найдётся такое числ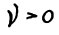о , что

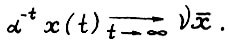
(3.2)

Докажем сначала два вспомогательных утверждения.

Для простоты и, согласно примечанию к § 1.1, не умаляя общности, будем далее считать, что α = 1. Тогда, как известно, 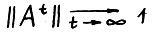, так что найдётся натуральное l, такое что 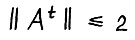для t ≥ l. Из примитивности матрицы A также следует, что для любого δ > 0 функция 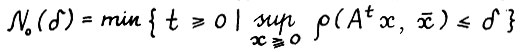имеет конечное значение. Положим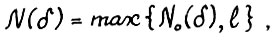

Лемма 3.1. Найдётся константа a &62; 0, такая что для любых 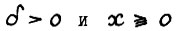выполняется .

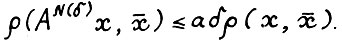Доказательство. Для любого вектора x ≥ 0 обозначим 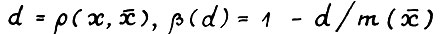. Поскольку 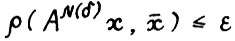для всех x ≥ 0, то можно считать, что 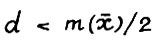- в противном случае достаточно взять .

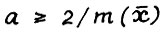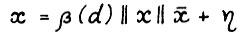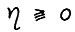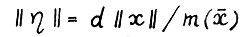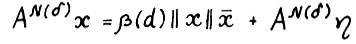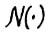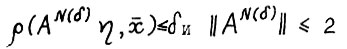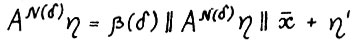Очевидно, вектор x ≥ 0 можно представить в виде , где , , так что . Аналогично, так как по определению функции выполняется , то , где 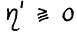, 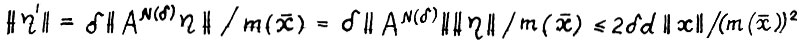. Итак, поскольку используемая здесь норма аддитивна на 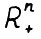и 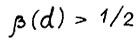, имеем 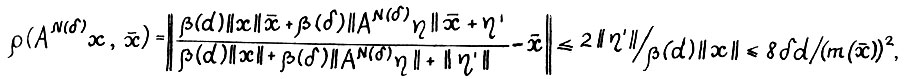что и требовалось. Лемма доказана.

Лемма 3.2.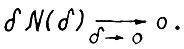

Доказательство. Фиксируем некоторое значение 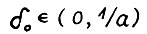и положим 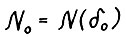. Для любого x ≥ 0 имеем 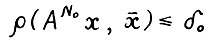, следовательно, по лемме 3.1 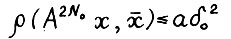для x ≥ 0, аналогично 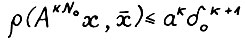, для всех 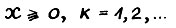(3.3)

Ясно, что для любого 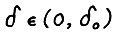найдётся натуральное К(δ), такое что 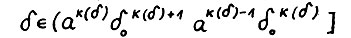. Тем самым, по определению N(δ) и в силу (3.3) 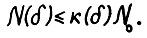. Таким образом 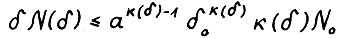. Стремление δ к нулю означает, что соответствующее 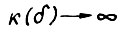. Отсюда, поскольку 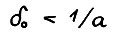, имеем 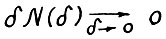. Лемма доказана.

Доказательство теоремы 3.1.

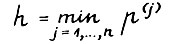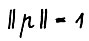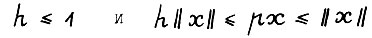Обозначим . Так как , то для любого x ≥ 0. Фиксируем ε > 0, такое что для 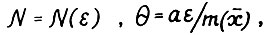, где a - константа из леммы 3.1, выполняется

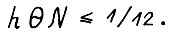
(3.4)

Заметим, что существование такого числа ε следует из леммы 3.2.

Рассмотрим произвольный скользящий план 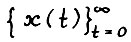, удовлетворяющий условиям теоремы. Возьмём произвольный момент τ ≥ r, где, как и в § 2, число r есть наименьший показатель степени, такой чтo 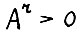. Обозначим 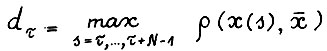. В силу теоремы 2.1 найдется натуральное T(ε), такое что если T₀ ≥ T(ε), то 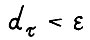. Положим 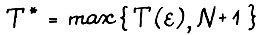, пусть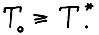

Обозначим 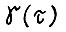максимальное значение целевой функции в задаче вида (3.1), решаемой на шаге 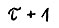скользящего планирования. Тогда, если 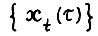- оптимальная траектория, являющаяся решением этой задачи, то 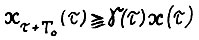и по определению 4 имеет место 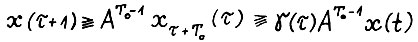. По лемме 3.1 и выбору Т₀ имеем 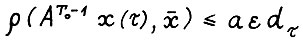, так что справедливо

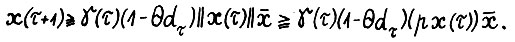
(3.5)

Аналогично (2.6) положим 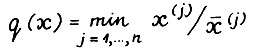. Поскольку рассматриваемая здесь модель является частным случаем модели 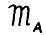, то для функционала q выполняются с соответствующими изменениями все утверждения теоремы 2.2.

Рассмотрим точку 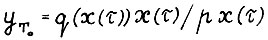. Ясно, что в неё можно за Т₀ шагов попасть из точки 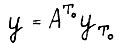(т.е. найдётся допустимая траектория 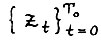, такая, что 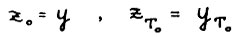). Так как 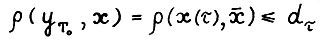, то по лемме 3.1 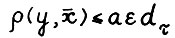. Отсюда, как легко показать, 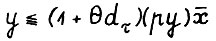. Так как р - собственный вектор матрицы А, то 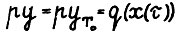и значит 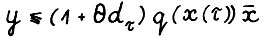. Поскольку 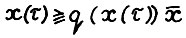, то отсюда и так как в рассматриваемой модели,очевидно, выполняется условие свободного расходования, следует, что из точки х(τ) можно за Т₀ шагов попасть в точку 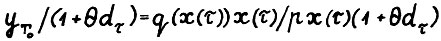. Следовательно, поскольку 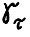- максимальное значение целевой функции в (3.1), имеем

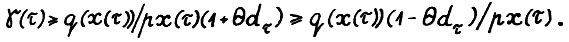
Таким образом, в силу (3.5) и поскольку 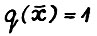, выполняется 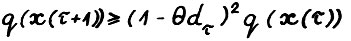. Повторяя рассуждения применительно к моментам 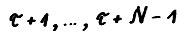, получим

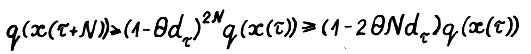
(3.6)

для всех

Последнее в цепочке неравенств (3.6) следует из (3.4) и сравнения производных по 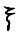функций 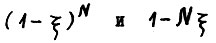, равных между собой при .

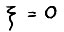Положим 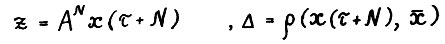, так что по лемме 3.1. 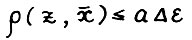, тем самым

Следовательно, учитывая (3.4), 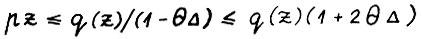. Так как скользящий план является допустимой траекторией, то 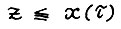и значит 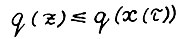. Таким образом, справедливо

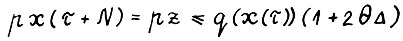
(3.7)

Заметим, что 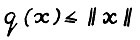для любого x ≥ 0, поскольку, очевидно, 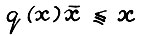. Отсюда, благодаря свойствам используемой здесь нормы, имеем

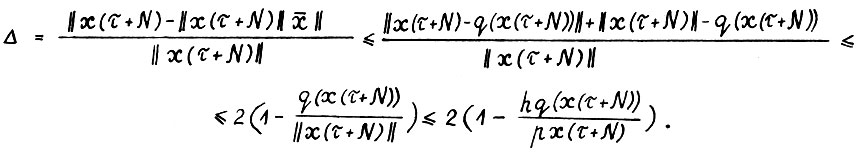
Следовательно, в силу (3.7), (3.6) и (3.4) и так как h ≤ 1, справедливо

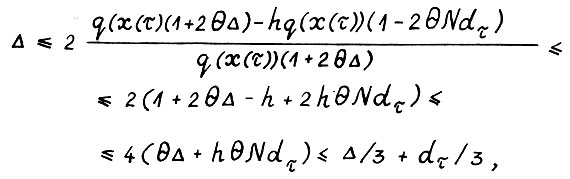
, так что

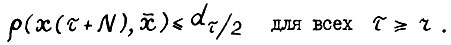
(3.8)

Отсюда, в частности, 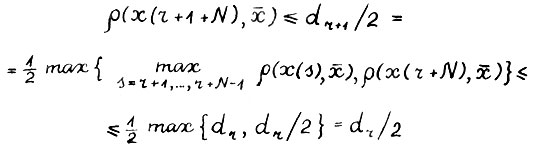. Аналогичным образом можно последовательно показать выполнение 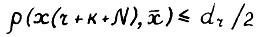для к = 2,3,...,N-1. Таким образом в силу (3.8) 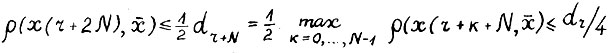. Рассуждая аналогичным образом, получим

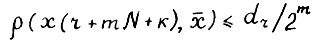
для всех m = 1,2,... ; k = 0,1,...,N-1, т.е.

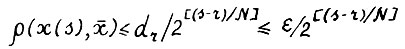
(3.9)

для всех 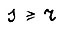, где 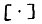- обозначение целой части числа. Обозначим 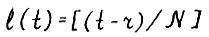, тогда для любого 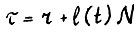по свойству эффективного функционала, используя формулу (3.6) последовательно для 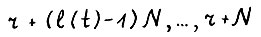, получим

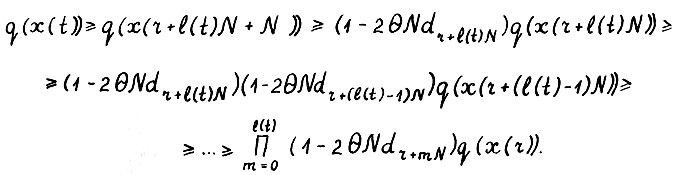
Отсюда в силу (3.9) следует 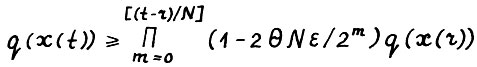для 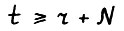. Легко видеть, что при произведение сходится к положительной величине. Применяя следствие 2.2 из § 2 нетрудно показать, что при выбранном Т(ε) справедливо 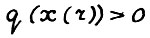. Таким образом рассматриваемый скользящий план строго отделён от нуля, что вместе с (3.9) доказывает теорему.