2.2. Доказательство теоремы 2.1.

Возьмём произвольный момент 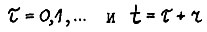. Для любого 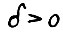, если 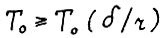в силу следствия 2.2 справедливо 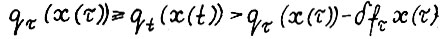. Отсюда и вследствие (2.6) в представлении

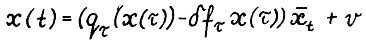
(2.8)

вектор υ положителен.

Далее доказательство будет следовать итеративной схеме, сходной с использованной в § 1.3 при доказательстве теоремы 1.1. Сначала будет найдена оценка для величины 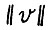, точнее, такая константа в > 0, что 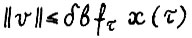. Тем самым, исходя из представления (2.8), можно аналогичным образом оценить величину 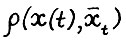, при условии, что дробь 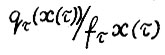отделена от нуля некоторой константой.

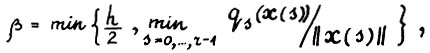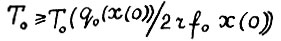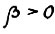Положим , где h - константа из леммы 1.4. В силу следствия 2.2, если горизонт T₀ достаточно велик (например, ), то . Легко видеть, что для τ = 0,1,...,r-1 выполняется 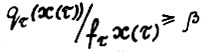. Следовательно, согласно приведённым выше рассуждениям, для 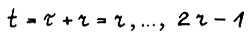и любого ε > 0 при достаточно малом δ cправедливо 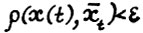, а тем самым - в силу теоремы 2.2(3°) - и требуемое (2.2). Далее будет показано, что из неравенства 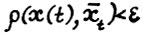для 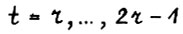следует, что 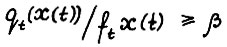. Тем самым, повторяя рассуждения, можно доказать выполнение (2.2) для 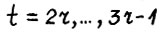и т.д. для любого натурального t.

Перейдём к изложению доказательства. В силу (2.8) можно записать

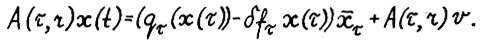
(2.9)

Так как по допустимости скользящего плана 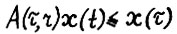, то 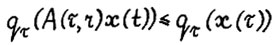. Отсда и из (2.9) имеем

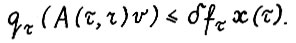
(2.10)

В силу A.2.1, (2.6) и (2.5) справедливо и 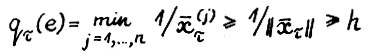. Таким образом из (2.10) получим искомую оценку 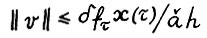. Отсюда и из представления (2.8),используя (2.5) можно записать

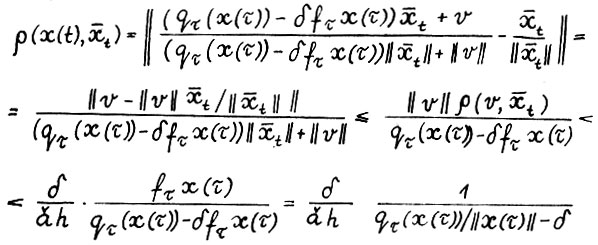
Заметим, что если взять 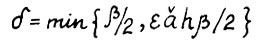и выполняется 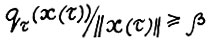, то для любого ε > 0 отсюда следует 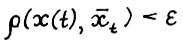при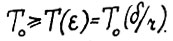

Поскольку момент t был выбран произвольным образом и так как по теореме 2.2(3°) справедливо 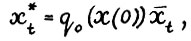t ≥ r, то для завершения доказательства достаточно отметить два обстоятельства:

1) по определению числа 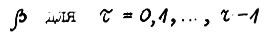справедливо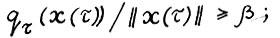

2) из неравенства 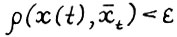следует 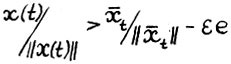. Отсюда, используя (2.6), (2.5) и (2.3), получим 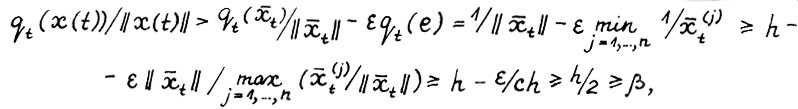так как, не умаляя общности, можно считать 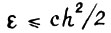. Теорема доказана.