
§ 2. Динамическая меиотраслевая модель с переменными матрицами
2.1. Формулировка модели и результаты
Рассмотрим модель 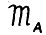 - частный случай модели
- частный случай модели 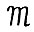 , когда технологические множества имеют вид:
, когда технологические множества имеют вид: 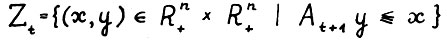 , где
, где 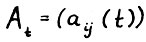 - неотрицательная квадратная матрица размерности n*n, элементы
- неотрицательная квадратная матрица размерности n*n, элементы 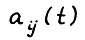 которой интерпретируются как коэффициенты затрат продукции i-й отрасли на выпуск единицы продукции j-й отрасли в периоде t. При этом
которой интерпретируются как коэффициенты затрат продукции i-й отрасли на выпуск единицы продукции j-й отрасли в периоде t. При этом 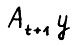 есть вектор продукции, затрачиваемой на вектор выпуска y в периоде t + 1, эти затраты покрываются за счёт выпуска х в предыдущем периоде и не должны превосходить его.
есть вектор продукции, затрачиваемой на вектор выпуска y в периоде t + 1, эти затраты покрываются за счёт выпуска х в предыдущем периоде и не должны превосходить его.
Таким образом, траектория 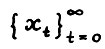 в рассматриваемой модели является допустимой, если и только если выполняется
в рассматриваемой модели является допустимой, если и только если выполняется
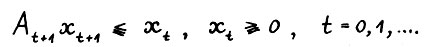
(2.1)
Модель 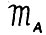 является упрощённым вариантом модели Неймана-Леонтьева - одной из первых, для которых (в стационарном случае:
является упрощённым вариантом модели Неймана-Леонтьева - одной из первых, для которых (в стационарном случае: 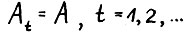 ) была доказана теорема о магистрали /32/. Б работе /28/ свойство магистральности было доказано для рассматриваемой здесь модели с изменяющимися матрицами при условии кх равномерной ограниченности, формулируемом ниже.
) была доказана теорема о магистрали /32/. Б работе /28/ свойство магистральности было доказано для рассматриваемой здесь модели с изменяющимися матрицами при условии кх равномерной ограниченности, формулируемом ниже.
А.2.1. найдутся матрицы 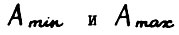 , размерности
, размерности 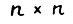 , причем
, причем 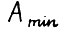 - примитивная*, такие что для t = 1,2,... справедливо
- примитивная*, такие что для t = 1,2,... справедливо
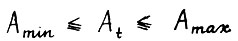
* (См. /3, глава XIII/.)
Известно /3, глава XIII/, что найдётся натуральное r, такое что 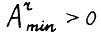 . Обозначим через
. Обозначим через 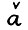 минимальный элемент матрицы
минимальный элемент матрицы  , через
, через 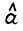 - максимальный элемент матрицы
- максимальный элемент матрицы 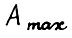
Везде далее в этом параграфе будем считать предположение А.2.1 выполненным.
Легко видеть, что модель 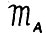 удовлетворяет всем условиям, наложенным в § 1 на модель
удовлетворяет всем условиям, наложенным в § 1 на модель 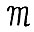 , кроме условий равномерной выпуклости А.1.4. В противоположность этому условию технологические множества Zt в модели
, кроме условий равномерной выпуклости А.1.4. В противоположность этому условию технологические множества Zt в модели 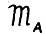 являются многогранными конусами. Однако при выполнении предположения А.2.1 здесь также справедливо утверждение о приближённой оптимальности скользящего планирования, аналогичное теореме 1.1.
являются многогранными конусами. Однако при выполнении предположения А.2.1 здесь также справедливо утверждение о приближённой оптимальности скользящего планирования, аналогичное теореме 1.1.
Теорема 2.1.
Для любого ε > 0 существует натуральное Т(ε), такое что для всякого скользящего плана 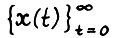 с горизонтом Т0 ≥ Т(ε) и начальным состоянием х(0) > 0 и любой оптимальной
с горизонтом Т0 ≥ Т(ε) и начальным состоянием х(0) > 0 и любой оптимальной 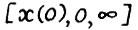 - траектории
- траектории 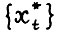 выполняется
выполняется
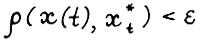
(2.2)
для 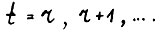
Замечание. Поскольку умножение матрицы Аt на скаляр не повлияет на соотношения координат векторов оптимальных траекторий, то утверждение теоремы сохранит силу, если предположение А.2.1 видоизменить следующим образом: 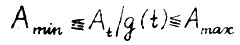 , где q(t) - числовая функция с положительными значениями (функция масштаба).
, где q(t) - числовая функция с положительными значениями (функция масштаба).
Доказательство теоремы 2.1 помещено в § 2.2. Общая идея доказательства та же, что и в § 1. Оно также основано на теореме о магистрали (доказываемой здесь с помощью той же техники, что и в /28/) и использует понятие эффективного функционала, причем в данном случае эффективные функционалы удаётся аналитически выразить через равновесные векторы выпуска.
Введём следующие обозначения 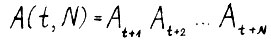 - произведение матриц, где N - натуральное число; С(t, N) - конус, состоящий из векторов вида
- произведение матриц, где N - натуральное число; С(t, N) - конус, состоящий из векторов вида 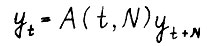 , где
, где 
Известно /20/, что если 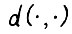 - проективная метрика в
- проективная метрика в 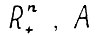 - матрица размерности мха с положительными элементами, то оператор А является сжимающим в проективной метрике в
- матрица размерности мха с положительными элементами, то оператор А является сжимающим в проективной метрике в 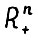 , т.е. найдётся константа
, т.е. найдётся константа 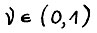 , такая что
, такая что 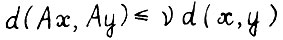 для любых
для любых 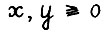 . Кроме того, известно, чтд величина
. Кроме того, известно, чтд величина 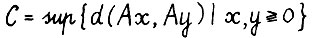 конечна. Исходя из этих фактов, в /29/ для проективной метрики вида
конечна. Исходя из этих фактов, в /29/ для проективной метрики вида 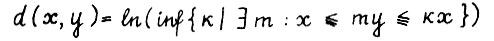 при выполнении предположения А.2.1, доказано следующее утверждение.
при выполнении предположения А.2.1, доказано следующее утверждение.
Лемма 2.1. Существуют положительные константы ν > 0 и C, для которых справедливо 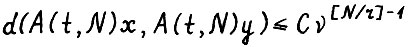 для любых
для любых 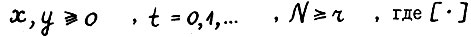 - целая часть числа.
- целая часть числа.
Отметим, что этот результат может быть применён при доказательстве утверждений о близости между векторами в угловой метрике, поскольку имеет место
Лемма 2.2.* Пусть 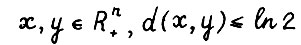 . Тогда выполняется
. Тогда выполняется 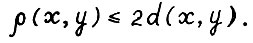 . Из леммы 2.1, в частности, следует, что для любого номера предел
. Из леммы 2.1, в частности, следует, что для любого номера предел 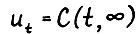 убывающей последовательности вложенных конусов
убывающей последовательности вложенных конусов 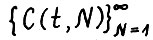 является лучом с вершиной в нуле, лежащим в
является лучом с вершиной в нуле, лежащим в 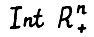 .
.
* (Доказательства этого и всех последующих утверждений параграфа приведены в § 2.3.)
Лемма 2.3. Для любого 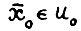 существует единственная последовательность
существует единственная последовательность 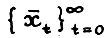 , такая что
, такая что 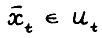 . При этом найдётся такое положительное число c, что
. При этом найдётся такое положительное число c, что
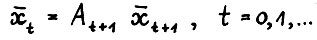
(2.3)
Для удобства будем далее считать, что 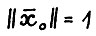 . Очевидно,
. Очевидно, 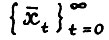 является допустимой траекторией.
является допустимой траекторией.
Возьмём n-мерный вектор-строку 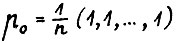 и рассмотрим последовательность
и рассмотрим последовательность 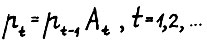 . Поскольку
. Поскольку 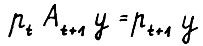 , то для любого допустимого (в смысле выполнения (2.1)) процесса
, то для любого допустимого (в смысле выполнения (2.1)) процесса 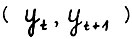 имеет место
имеет место 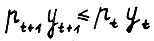 . При этом
. При этом 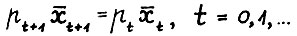 .
.
Обозначим 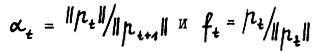 . Ясно, что последовательности
. Ясно, что последовательности 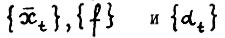 удовлетворяют (1.2) - (1.5), т.е. образуют разновесную систему. Нетрудно доказать, что последовательность
удовлетворяют (1.2) - (1.5), т.е. образуют разновесную систему. Нетрудно доказать, что последовательность 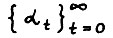 ограничена сверху и снизу некоторыми положительными константами (
ограничена сверху и снизу некоторыми положительными константами (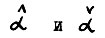 , соответственно). Действительно, в силу А.2.1 имеем:
, соответственно). Действительно, в силу А.2.1 имеем:
1) 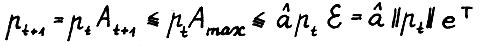 , откуда
, откуда 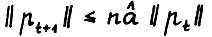 , так что
, так что
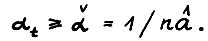
(2.4)
2) 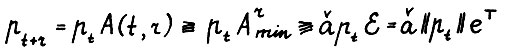 , следовательно,
, следовательно,  , откуда в силу (2.4)
, откуда в силу (2.4) 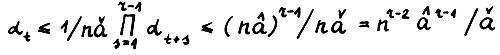 . Итак
. Итак 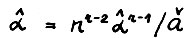 .
.
Следовательно, если заменить модель 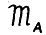 эквивалентной ей
эквивалентной ей 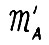 , где матрица Аt заменяется на
, где матрица Аt заменяется на 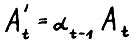 , то если положить
, то если положить 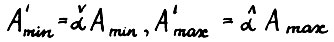 , то
, то 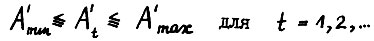
Отсюда и из рассуждения в примечании к § 1.1 следует, что, не умаляя общности, можно считать αt = 1 для t = 0,1,... и тем самым 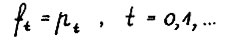
Справедливо утверждение, аналогичное лемме 1.2:
Лемма 2.4.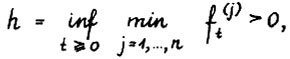 а также его следствие, в доказательстве которого в § 1 предположение А.1.4 о равномерной выпуклости не использовалось:
а также его следствие, в доказательстве которого в § 1 предположение А.1.4 о равномерной выпуклости не использовалось:
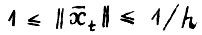
(2.5)
Положим для любого 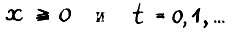
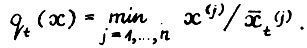
(2.6)
Заметим, что 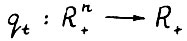 тогда и только тогда, когда х > 0. Легко видеть, что каждый функционал
тогда и только тогда, когда х > 0. Легко видеть, что каждый функционал 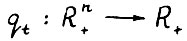 , задаваемый формулой (2.6), положительно однороден, вогнут, непрерывен и монотонен.
, задаваемый формулой (2.6), положительно однороден, вогнут, непрерывен и монотонен.
Теорема 2.2.
Пусть 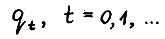 - функционалы,запзглые формулой (2.6), тогда справедливы следующие утверждения:
- функционалы,запзглые формулой (2.6), тогда справедливы следующие утверждения:
1°. Последовательность функционалов 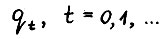 является эффективной (см. определение 5).
является эффективной (см. определение 5).
2°. Для любых 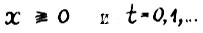 выполняется
выполняется
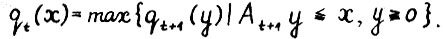
(2.7)
3°. 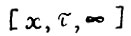 - траектория
- траектория 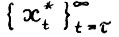 - является оптимальной тогда и только тогда, когда на ней в каждом периоде t функционал qt достигает условного максимума вида (2.7), т. е.
- является оптимальной тогда и только тогда, когда на ней в каждом периоде t функционал qt достигает условного максимума вида (2.7), т. е. 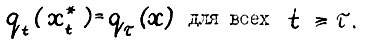
Кроме того, если 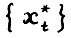 оптимальна, то для
оптимальна, то для 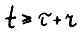 (где r - минимальный показатель, такой что
(где r - минимальный показатель, такой что 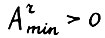 ) выполняется
) выполняется
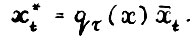
40. Функционалы 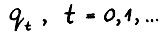 равностепенно липшицевы с константой 1/с, где с - величина из леммы 2.1,т.е. для любых
равностепенно липшицевы с константой 1/с, где с - величина из леммы 2.1,т.е. для любых 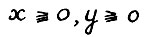 имеет место
имеет место
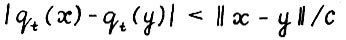
для t = 0,1,... .
Лемма 2.5. Пусть 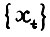 - оптимальная
- оптимальная 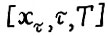 - траектория,
- траектория, 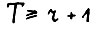 , тогда для
, тогда для 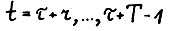 выполняется
выполняется 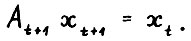
Из леммы 2.3, определения последовательности 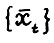 и лемм 2.1 и 2.2 непосредственно следует утверждение, которое можно назвать теоремой о магистрали.
и лемм 2.1 и 2.2 непосредственно следует утверждение, которое можно назвать теоремой о магистрали.
Теорема 2.3. Для любого ε > 0 найдётся натуральное l(ε), такое что если 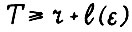 , то для всякой оптимальной траектории
, то для всякой оптимальной траектории 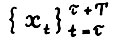 , где
, где 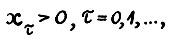 выполняется
выполняется
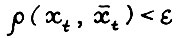
где 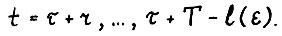
Заметил, чтo доказательства следствия 1.1 и предложения 1.2 в § 1 сохраняют силу и в данном случае, тем самым имеет место
Следствие 2.1. Для любого δ > 0 существует такое натуральное 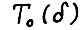 , что для всякой оптимальной траектории
, что для всякой оптимальной траектории 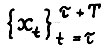 , где
, где 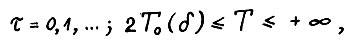 выполняется
выполняется
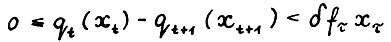
для 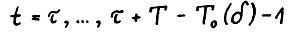
Отсюда, согласно определению 4 и так как для любого допустимого процесса (x,y) выполняется 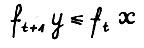 , легко получить
, легко получить
Следствие 2.2. Для любого 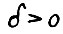 , натурального N всякого скользящего плана
, натурального N всякого скользящего плана 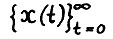 с горизонтом
с горизонтом 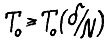 где T0(⋅) - из следствия 2.1, выполняется
где T0(⋅) - из следствия 2.1, выполняется 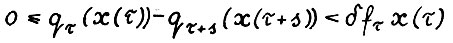 для любых
для любых 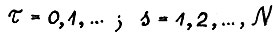
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'