1.4. Доказательство вспомогательных утверждений

Как и прежде, везде в доказательствах, не умаляя общности, считаем, что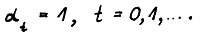

Докажем сначала лемму 1.2, так как следующее из неё неравенство (1.15) будет использовано при доказательстве других утверадений.

Доказательство леммы 1.2.

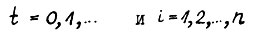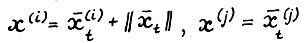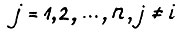Возьмём произвольные . Рассмотрим вектор х , такой что для . В силу (1.1) имеем 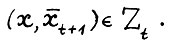. Применяя А.1.5, можно записать 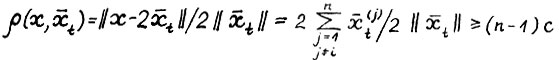. Отсюда вследствие (1.7), обозначив 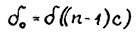, получим 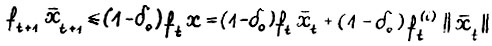. Следовательно, в силу (1.5), A.1.5. и (1.2) 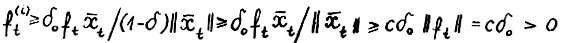. Поскольку координата i была выбрана произвольно, лемма доказана.

Доказательство леммы 1.1.

Прежде всего заметим, что если 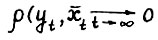, т.е. найдется ε > 0 такое, что для некоторой подпоследовательности 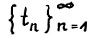выполняется 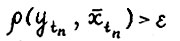, то в силу (1.7) справедливо 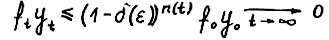, где n(t) - количество членов последовательности 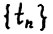, не превосходящих t. Отсюда 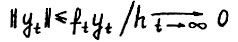, так что утверждение леммы выполнено.

Таким образом остаётся рассмотреть случай, когда 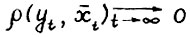. В силу (1.4) последовательность 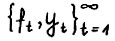не возрастает и потому сходится. Положим 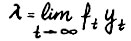. Поскольку 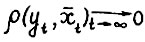и так как по лемме 1.2 последовательность 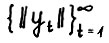ограничена сверху 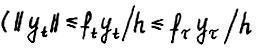, имеем 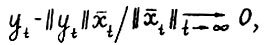, , откуда 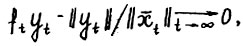, так что, учитывая (1.15), 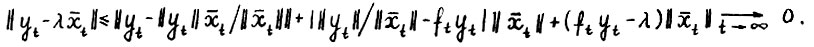. Лемма доказана

Доказательство теоремы 1.2.

1⁰. Положительная однородность и вогнутость эффективных функционалов непосредственно следует из того, что технологические множества являются выпуклыми конусами с вершинами в нуле. Докажем свойство монотонности. Пусть 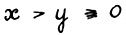. Возьмём произвольное натуральное τ. Так как x - y > 0, то очевидно существует такое число 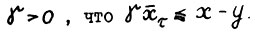. Отсюда в силу положительной однородности, вогнутости эффективных функционалов, условия A.1.3 и (1.11) имеем 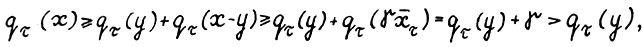что и требовалось.

2°. Как отмечалось, 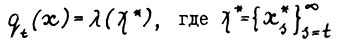есть оптимальная 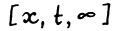- траектория. Тем самым по лемме 1.1 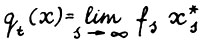. Вследствие условия равномерной выпуклости А.1.4 бесконечная оптимальная траектория, исходящая в момент t + 1 из точки 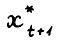совпадает, начиная с этого мо-мента, с траекторией 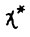, так что

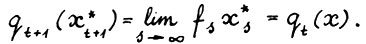
(1.30)

Возьмём теперь произвольный вектор y, такой что 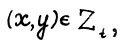и оптимальную 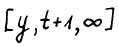- траекторию 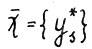. Тогда 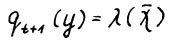. Рассмотрим допустимую траекторию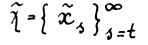, где 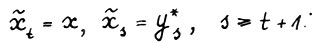. По оптимальности траектории 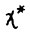справедливо 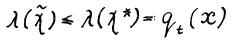. В то же время, очевидно, 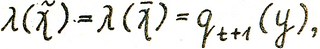, следовательно 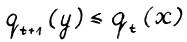, что вместе с (1.30) даёт доказываемое (1.12).

Для ясности заметим, что если отказаться от принятого в доказательствах условия 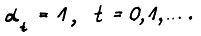, то получим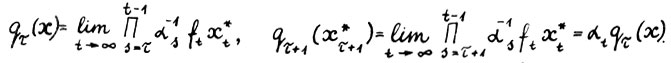

3°. Последовательно применяя (1.30) для 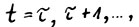получим, что для оптимальной траектории 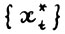имеет место 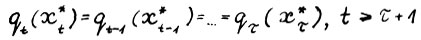, тем самым выполнение (1.13) является необходимым условием оптимальности траектории. Докажем достаточность. Пусть для траектории 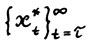выполняется (1.13), требуется доказать, что она оптимальна. Предположил противное, т.е. (см. определение 3) найдётся допустимая 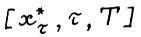- траектория 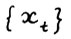, такая чтo 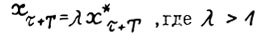. Следовательно,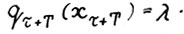 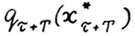или в силу (1.13) 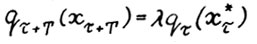. В то же время, вследствие (1.12) имеет место 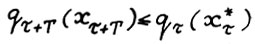- противоречие. Тем самым 3° доказано.

4°. Возьмём произвольные t = 0,1,... и векторы 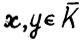положим 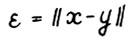. Тогда по определению конуса 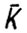имеем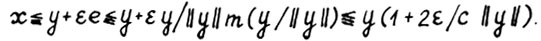

Пусть для определённости 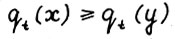, тогда в силу монотонности q_t получим 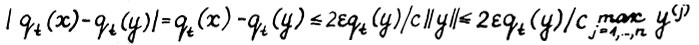. Вследствие А.1.5 и (1.15) можно записать 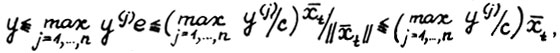, так что 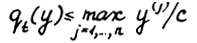и 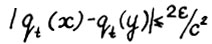. Таким образом, искомая L = ²/_c². Теорема доказана.

Доказательство леммы 1.3.

Предположим противное, т.е. существуют такие допустимая 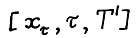- траектория 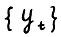и момент t₀, что 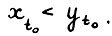. Тогда, очевидно, найдётся число λ > 0, такое что 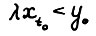, и в силу условия А.1.3 и конусности технологических множеств найдётся допустимая 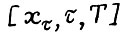- траектория 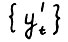, такая что 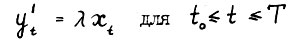. Получено противоречие оптимальности траектории 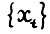. Лемма доказана.