1.3. Доказательство основного результата

Докажем сначала ряд вспомогательных утверждений.

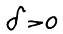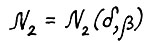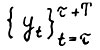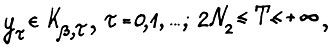Предложение 1.2. Для любого существует такое натуральное , что для всякой оптимальной траектории , где справедливо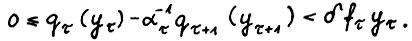

Доказательство. Пусть в формулировке следствия 1.1 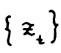есть оптимальная 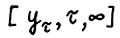- траектория, так что по теореме 1.2 (3°) справедливо 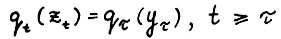. Возьмём произвольное 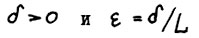, где L - константа Липшица из теоремы 1.2 (4°). В силу следствия 1.1 найдётся натуральное 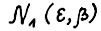, такое что если горизонт 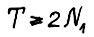, то для 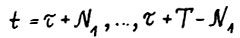имеет место 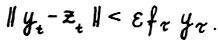. Кроме того, по теореме 1.3 для тех же t выполняется 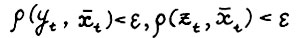, так что вследствие А.1.5, очевидно, 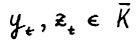(не умаляя общности, считаем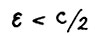

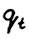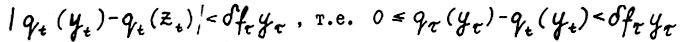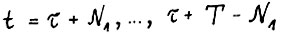). Следовательно, можно применить теорему 1.2 (4°). Тогда благодаря положительной однородности , получим для . Отсюда, в силу (1.12) немедленно следует доказываемое, если положить 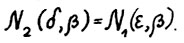. Предложение доказано.

Предложение 1.3. Возьмём произвольные 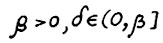и натуральное 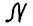. Пусть 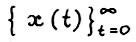скользящий план с горизонтом 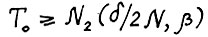, где 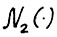- из предложения 1.2. Тогда для любого момента τ, для которого 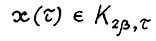справедливо 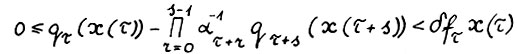при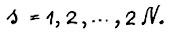

Доказательство. Так как 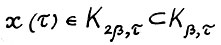,то при выполнении условий данного предложения в силу определения 4 и предложения 1.2 справедливо

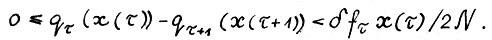
(1.27)

Отсюда, применяя (1.4), так как 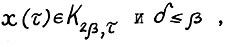, можно написать 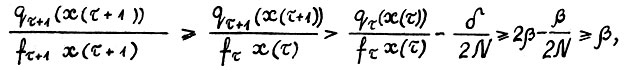, т.е. 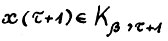. Следовательно, можно снова использовать предложение 1.2, в результате чего получим 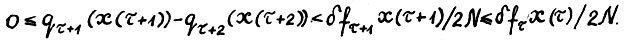. Сложение этого неравенства с (1.27) даёт 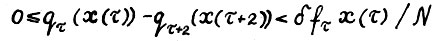. Рассуждая далее аналогичным образом, можно доказать выполнение требуемого (1.26) для всех 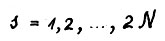. Предложение доказано.

Таким образом, на протяжении заданного числа периодов, начиная с произвольного фиксированного момента τ, скользящий план с достаточно большим горизонтом Т₀ обеспечивает достижение значений соответствующих эффективных функционалов 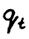, отличающихся от их максимальных значений не более,чем на указанную величину. Докажем теперь, что сами решения, получаемые в скользящем плане, также близки к оптимальным решениям, т.е. доставляющим максимум соответствующим эффективным функционалам (этот факт будет непосредственно использован для доказательства теоремы 1.1).

Предложение 1.4. Возьмём произвольное малое 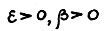и натуральное 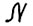. Найдётся такое натуральное 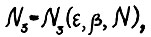что для скользящего плана 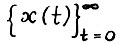с горизонтом 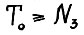справедливо следующее: для любого момента τ, для которого 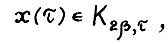выполняется 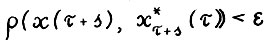при 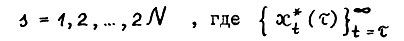- оптимальная 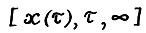- траектория.

Доказательство. Пусть 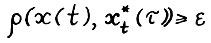для некоторого 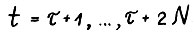, тогда в силу условия равномерной выпуклости А.1.4, а также вследствие конусности 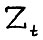, для любого вектора y, такого что 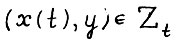справедливо

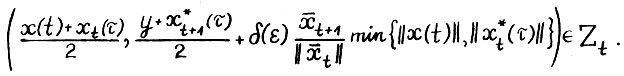
Тем самым из точки 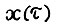можно за 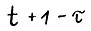шагов попасть в точку 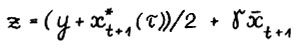, где 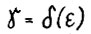*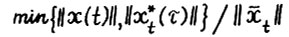. Заметим, что в силу (1.2), (1.4), (1.10) и леммы 1.1 можно написать 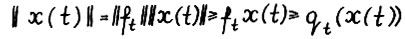. Аналогично, используя также (1.12), получим 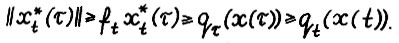. Отсюда и вследствие (1.15) справедливо 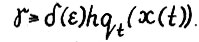. Пусть на векторе y достигается 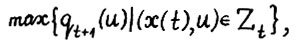, тогда в силу (1.12) и (1.11) имеет место 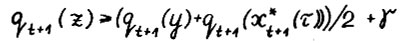. Oтсюда и так как 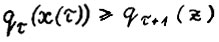, имеем 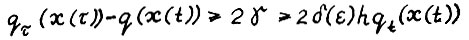или после перегруппировки 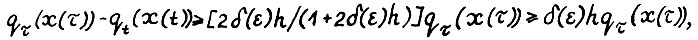считая без ущерба для общности, что 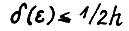. По условию 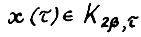и следовательно, 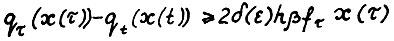. Для завершения доказательства, методом от противного достаточно применить предложение 1.3, положив 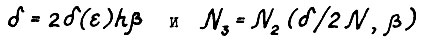. Предложение доказано.

Доказательство теоремы 1.1.

Пусть 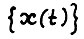- скользящий план и 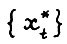- оптимальная 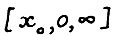- траектория из формулировки теоремы. Обозначим через 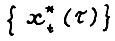оптимальную 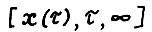- траекторию так что для τ = 0 эта траектория совпадает с .

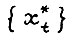Идея доказательства состоит в последовательном применении итеративной схемы, на каждой итерации которой рассматривается отрезок времени длиной 2N, где N - натуральное число, подбираемое исходя из теоремы о магистрали. На начальном шаге непосредственно с помощью предложения 1.4 устанавливается справедливость доказываемого неравенства (1.9) для моментов t = 1,2,...,2N. При переходе к следующей итерации рассматриваемый отрезок времени сдвигается вперёд на N периодов. Выполнение (1.9) для первых N из рассматриваемых моментов следует из предыдущей итерации, а для последних N сначала с помощью предложения 1.4 доказывается близость скользящего плана к траектории 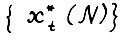, откуда, с помощью теоремы о магистрали и неравенства треугольника также устанавливается (1.9). После этого осуществляется переход к следующей итерации и т.д.

Следует обратить внимание, что в формулировках используемых здесь предложения 1.4 и теоремы 1.3 накладываются определённые условия на вектор начального состояния - он должен принадлежать некоторому конусу вида 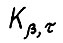. Поэтому основным техническим моментом при осуществлении изложенной схемы доказательства является такой подбор горизонта Т₀ и вспомогательных параметров β и N, который бы обеспечил выполнение вышеупомянутых начальных условий для каждой её итерации.

Перейдём непосредственно к доказательству теоремы.

Возьмём произвольное малое ε > 0 (не умаляя общности, считаем 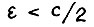, где c - константа из предположения А.1.5). Положим 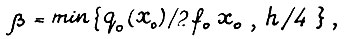, где h - константа из леммы 1.4,

N = N₀(^ε/₃,β) и 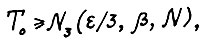, где 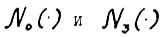определяются согласно теореме 1.3 и предложению 1.4, соответственно.

Положим τ = 0. Заметим, что по выбору β выполняется 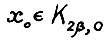, так что

1) Применяя предложение 1.4, получим

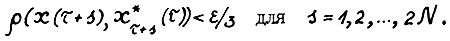
(1.28)

2) По теореме 1.3 и по выбору N для 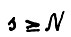справедливо Отсюда, из (1.28) и неравенства треугольника следует справедливость (1.9) для 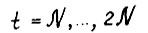(заметим, что при τ = 0 выполнение (1.9) для 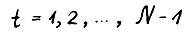следует непосредственно из (1.28)) и кроме того

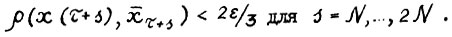
(1.29)

3) Из (1.29), а также (1.2), A.1.5 и (1.15) имеем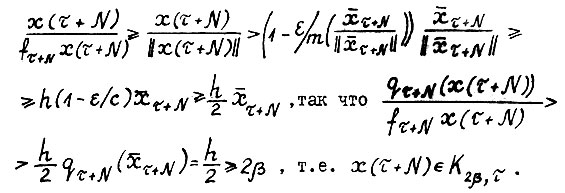

Таким образом, переобозначив 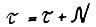и применяя снова этапы 1) - 2), получим (1.9) для 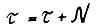и далее таким же образом для любого натурального t. Теорема доказана.