1.2. Теорема о магистрали

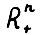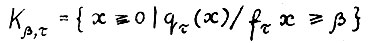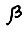Рассмотрим для каждого натурального τ выпуклый замкнутый конус, лежащий в , с вершиной в начале координат , где - произвольное положительное число, достаточно малое, чтобы множество 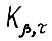было непустым. Смысл дроби 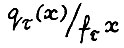прояснится, если сопоставить (1.10) и лемму 1.1. Ясно, что для любого х ∈ К_β,τ существует допустимая 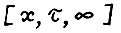- траектория, растущая темпом α;

Теорема 1.3. (о магистрали в сильной форме).

Для любого ε > 0 существует такое натуральное 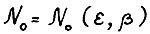, что для всех оптимальных [х_τ, τ, Т] - траекторий 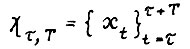, где 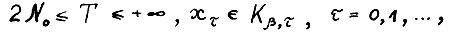имеет место

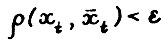
(1.14)

для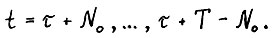

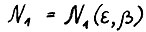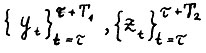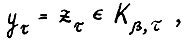
Следствие 1.1. Для любого ε > 0 существует такое натуральное , что для любых двух оптимальных траекторий где имеет место 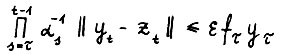для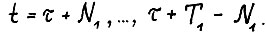

Замечание. Теорема 1.3 является усилением теоремы о магистрали, доказанной в /16, теорема 2/, в двух отношениях:

1) Оценка N₀(ε) является равномерной для всех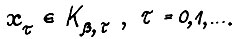

2) Отброшен ряд условий-технического характера, а именно, ограничение на вид целевой функции в определении оптимальных траекторий (см. определение 2) и условие, что последовательность функционалов 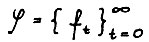из равновесной системы строго отделена от нуля по всем координатам - на самом деле этот факт следует из остальных предположений:

Лемма 1.2.

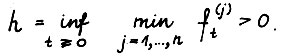
Следствие 1.2.

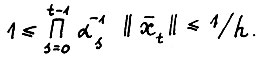
(1.15)

Действительно, в силу (1.2), (1.5) и (1.3) справедливо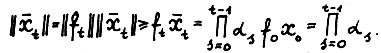

Далее, из леммы 1.2 имеем 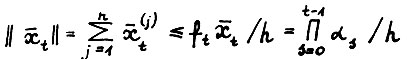Следствие доказано.

Сформулируем ещё одно вспомогательное утверждение, которое естественно назвать принципом оптимальности.

Лемма 1.3. Пусть 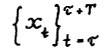- оптимальная 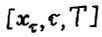- траектория, где τ - любое натуральное, 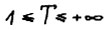. Тогда для любой допустимой 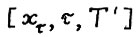- траектории 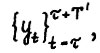где 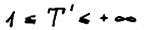, и любого 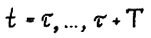(если Т = +∞, то для любого t ≥ τ) найдётся индекс i = 1,...,n, такой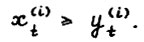

Замечание. В доказательстве этого утверждения (см. § 1.4) используются только условия А.1.1 - А.1.3, тем самым оно верно и в случае, когда технологические множества являются многогранными выпуклыми конусами.

Доказательство теоремы 1.3, как и доказательство соответствующей теоремы в /16/, будет проводиться в основном по стандартной схеме, выработанной X. Никайдо/12/, но со значительными отличиями в технических деталях, связанными с упомянутыми в замечании к теореме 1.3 обобщениями.

Докажем сначала следующий факт, обобщающий теорему о магистрали в слабой форме, доказанную в /17/.

Предложение 1.1. Для любого ε > 0 существует такое натуральное 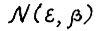, что в условиях теоремы 1.3 число М моментов, в которые выполняется 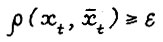, не превосходит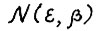

Доказательство. Возьмём произвольную точку 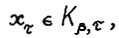, где 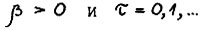- также произвольные. Пусть 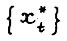- оптимальная 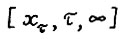- траектория, тогда из леммы 1.1,так как максимум в формуле (1.10) достигается на бесконечной оптимальной траектории, следует 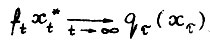Отсюда, учитывая (1.4), получим

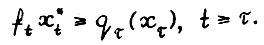
(1.16)

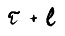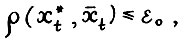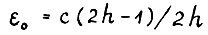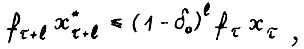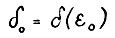Пусть - первый момент времени, в который выполняется неравенство где , с и h - константы из А.1.5 и леммы 1.2, соответственно. Тогда в силу (1.7) имеем где . Отсюда, из (1.16) и так как 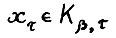, имеем 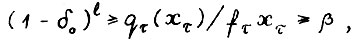или

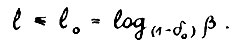
(1.17)

Заметим, что эта оценка справедлива для произвольных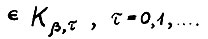

Далее, так как 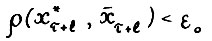, используя (1.15), А.1.5, (1.2), (1.16), и по выбору ε₀ получим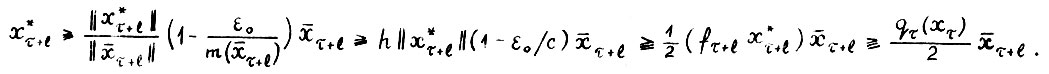

Таким образом, ввиду условия свободного расходования А.1.3 и оценки (1.17), для любого 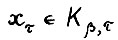и τ = 0,1,... существует допустимая 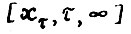- траектория 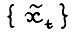, такая что 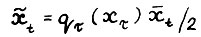для 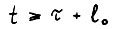. Пусть 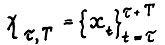- оптимальная 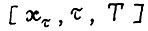- траектория, причём T ≥ l₀. Тогда в силу леммы 1.3 и А.1.5 найдётся индекс i = 1,2,3,...,n, такой что 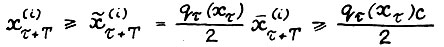откуда благодаря (1.15) имеем

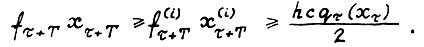
(1.18)

Для завершения доказательства остаётся заметить, что вследствие (1.7) для любого наперёд заданного ε > 0 справедливо 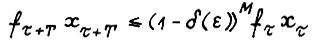, где М - число из формулировки предложения. Применяя (1.18), для произвольных 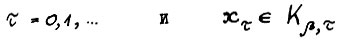получим 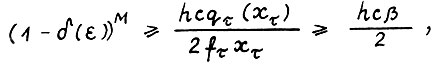или 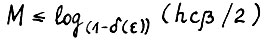. Предложение доказано.

Доказательство теоремы 1.3.

Зададимся произвольным ε > 0 и возьмём положительное 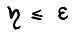, выбор которого будет далее уточнeн.

Из предложения 1.1 следует, что если горизонт планирования 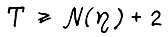, то найдётся не менее двух моментов времени t, в которые для оптимальной траектории 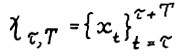выполняется

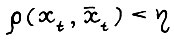
(1.19)

Пусть r и s - соответственно, первый и последний такие моменты на протяжении периода планирования. Заметим, что вследствие предложения 1.1 величины 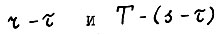ограничены числом 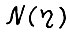независимо от длины периода планирования Т.

Рассмотрим произвольный промежуточный момент 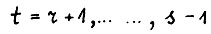, для которого 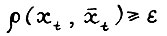(если такого t не существует, то утверждение теоремы автоматически выполняется). Тогда в силу (1.7)

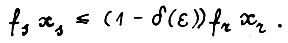
(1.20)

Легко показать, что векторы х_r и х_s можно представить в виде

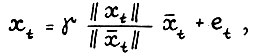
(1.21)

где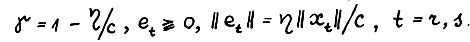

Отсюда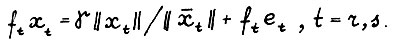

Применяя лемму 1.2 и её следствие, получим:

1)

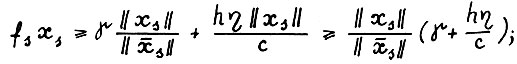
2)

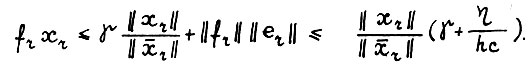
Отсюда и из (1.20) имеем

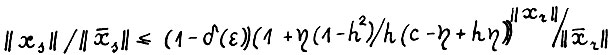
, то при 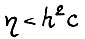не превосходит величины 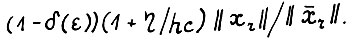. Таким образом 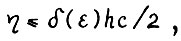, (1.22) то 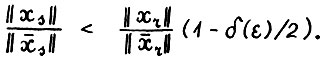. Отсюда, а также вследствие (1.21) и А.1.5 выполняется

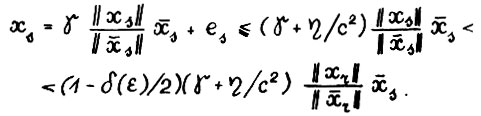
(1.23)

Ввиду (1.21), А.1.3 и конусности технологических множеств найдется допустимая 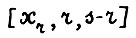- траектория 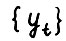, такая что 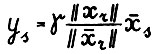. Заметим, что если 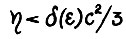, то поскольку 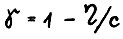и с ≤ 1, имеет место (^{1 - δ(ε)}/₂)* 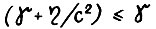и тем самым в силу (1.23) 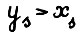, что вследствие леммы 1.3 противоречит оптимальности траектории 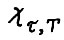. Таким образом, учитывая (1.22), если взять 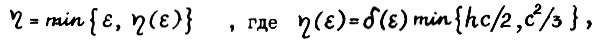, то в силу полученного противоречия во все промежуточные моменты 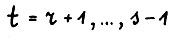выполняется требуемое (1.14). При этом, если положить 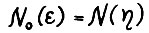, то как отмечалось, величины 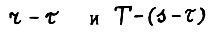не будут превосходить 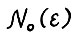. Теорема доказана.

Доказательство следствия 1.1.

Пусть в > 0 - произвольное число. Из теоремы 1.3 следует существование такого натурального 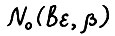, что если 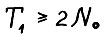, то

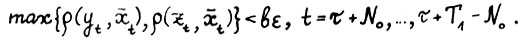
(1.24)

В силу леммы 1.2 для любого 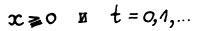выполняется 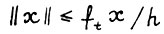так что вследствие (1.4) величины 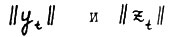ограничены сверху числом 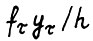.Следовательно, положив 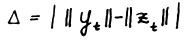можно написать

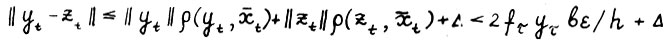
(1.25)

Пусть для определённости 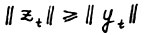, так что 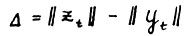.В силу (1.24) в представлениях 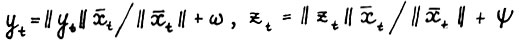имеет место 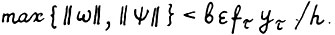. Вследствие леммы 1.3 найдётся индекс i = 1,2,...,n, такой что 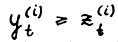. Отсвда, используя А.1.5, получим 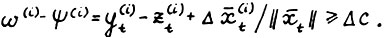. В то же время 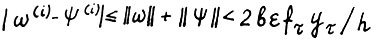. Следовательно, 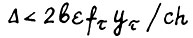и в силу (1.25) имеет место 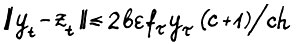. Таким образом, если положить 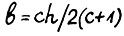и 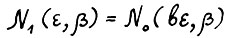, то получим доказываемое. Следствие доказано.