§ 1. Модель типа Неймана-Гейла с переменными строго выпуклыми технологическими множествам

1.1. Основные предположения и результаты

Пусть задана модель типа Неймана-Гейла 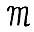, т.е. технологические множества 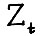, соответствующие периодам времени t = 0,1,..., являются выпуклыми замкнутыми конусами с вершинами в точке (0,0), лежащими в 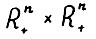и удовлетворяющими стандартным условиям:

А.1.1. Из 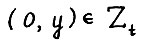следует y = 0 (при нулевых затратах выпуск равен нулю).

А.1.2.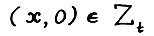 для любого x ≥ 0,

A.1.3.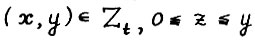 влечёт 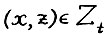(свободное расходование).

Заметим, что в силу А.1.1, А.1.2 и так как 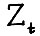- выпуклый конус, верна также импликация 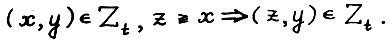(1.1)

Известно/10/, что при сделанных предположениях для любого начального вектора 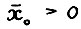существуют бесконечная оптимальная траектория 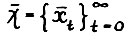и её характеристика, т.е. последовательности линейных функционалов (равновесных цен) 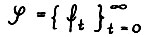и положительных чисел 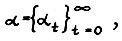такие что

(1.2)

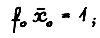
(1.3)

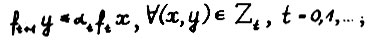
(1.4)

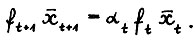
(1.5)

Тройку 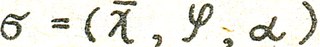будем называть равновесной системой.

Сделаем следующее важное предположение, которое можно назвать равномерной выпуклостью технологий^*.

^* (Аналогичные предположения о равномерной выпуклости используются в /13, 23/.)

А.1.4. Для любого 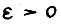существует число 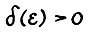, такое что при любом t = 0,1,... из условий 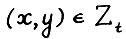, 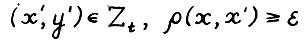следует

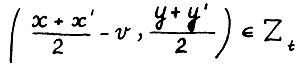
(1.6)

для любого вектора v ≥ 0, удовлетворяющего неравенству .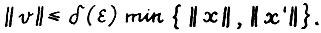

Из А.1.4 непосредственно следует, что система 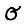является равномерно строго равновесной, точнее

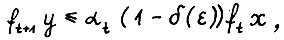
(1.7)

если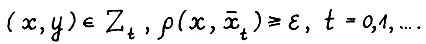

Замечания. 1) Сопоставим предположение А.1.4 с понятием равномерной выпуклости для множеств: подмножество 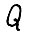множества Ε в нормированном пространстве называется равномерно выпуклым в Ε, если существует вещественная функция 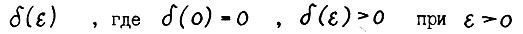такая что 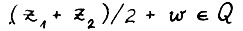для любых 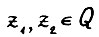и любого вектора 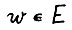, удовлетворяющего условию 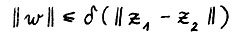. Нетрудно показать, что предположение А.1.4 будет выполнено, если потребовать, чтобы сечения технологических множеств 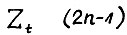-мерной гиперплоскостью 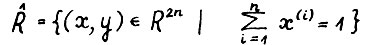были равномерно выпуклы в 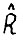, причём функция 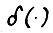не зависела от номера t.

2) Свойство технологии, выражаемое предположением А.1.4, иногда называют внешней экономией: одновременное использование разнообразных технологических процессов приводит к повышению совокупной эффективности. Если технологические множества задаются с помощью производственных функций Кобба-Дугласа: 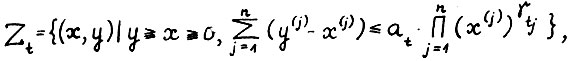где а_t - положительное число, 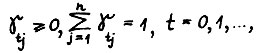то А.1.4 выполнено, когда эластичности 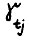всех факторов j = 1,2,...,n равномерно отделены от нуля по t = 0,1,...

3) Предположение о строгой выпуклости является единственным конструктивным, обеспечивающим выполнение условия строгости неймановского состояния равновесия (неравенство (1.7) представляет собой его обобщение на случай изменяющейся технологии), которое используется в большинстве работ,где доказывается теорема о магистрали для моделей типа Неймана-Гейла - см., например, /10, 12/. B частности, для рассматриваемой здесь модели в /16/ предполагается выполнение (1.7).

Пусть, кроме того, траектория 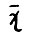равновесной системы равномерно положительна, т.е. выполняется

А.1.5.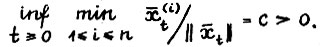

Везде далее в этом параграфе будем предполагать A.1.1 - А.1.5 выполненными.

Лемма 1.1.^* Для любой допустимой траектории 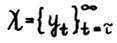имеет место

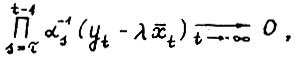
(1.8)

где 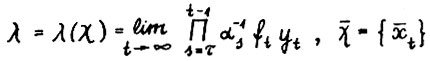- траектория из равновесной системы.

^* (Доказательство этой и всех последующих лемм параграфа приводится в § 1.4.)

В соответствии с леммой 1.1 будем говорить, что траектория 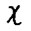, имеет темп роста 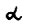, если 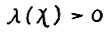. Этим свойством, в частности, обладает сама траектория 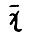,так как, очевидно, 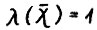. He составляет труда доказать (используя определение 3), что если из некоторой точки х исходит хотя бы одна допустимая траектория, имеющая темп роста 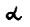, то бесконечная оптимальная траектория, исходящая из этой точки, также имеет темп роста 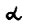. Таким образом, согласно лемме 1.1 все бесконечные допустимые траектории можно разбить на два класса: траектории, "отстающие" от бесконечных оптимальных, и траектории, имеющие темп роста 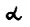, причём все траектории, принадлежащие ко второму классу, с течением времени сближаются (в смысле отраслевых пропорций).

Пусть задан вектор начального состояния х₀ и предположим, что для него выполняется А.1.6. Существует допустимая 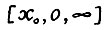- траектория, растущая с темпом .

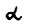Замечание. Это предположение, очевидно, выполняется, если x₀ > 0.

Пусть 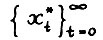есть бесконечная оптимальная траектория. Ввиду А.1.4 она единственна.

Основным результатом данного параграфа является

Теорема 1.1. Для любого 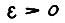существует натуральное Т(ε), такое что для всякого скользящего плана 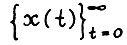с начальным состоянием x(0) = x₀ и горизонтом T₀ ≥ T(ε) имеет место

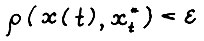
(1.9)

для t = 0,1,... .

Напомним, что согласно определению 4 всякий скользящий план "склеен" из начальных участков оптимальных траекторий. В доказательстве теоремы 1.1 (см. § 1.3) можно выделить два основных момента: 1) устанавливается факт слабой чувствительности этих участков по отношению к длине горизонта планирования и выбору терминальной целевой функции; 2) доказывается, что накопление "ошибок" на итерациях скользящего планирования не приводит к существенному отклонению получаемой траектории от бесконечной оптимальной. Доказательство опирается на приводимое в § 1.2 усиление известной теоремы о магистрали в сильной форме для модели с изменяющейся технологией /16/ и использует предложенное A.M. Рубиновым /14/ понятие эффективного функционала. Хотя это понятие было введено для модели с постоянной технологией, его можно естественным образом обобщить на случай изменяющейся технологии. А именно, рассмотрим величину

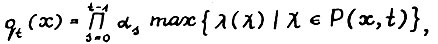
(1.10)

где P(x,t) - множество допустимых 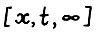- траекторий, λ(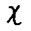) - величина из леммы 1.1, t = 0,1,... . Очевидно, максимум в формуле (1.10) достигается на оптимальной 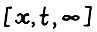- траектории (это следует непосредственно из леммы 1.1 и определения 3) и в частности,

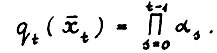
(1.11)

Заметим, что теперь предположение А.1.6 можно записать в виде:

Определение 5. Последовательность функционалов 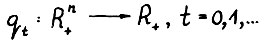, определённых формулой (1.10), называется эффективной. Соответственно, каждый функционал этой последовательности будем называть эффективным.

Эффективные функционалы обладают рядом весьма важных свойств. Формулируемая ниже теорема будет доказана в § 1.4.

Теорема 1.2. Пусть 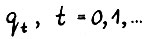- эффективная последовательность функционалов. Справедливы следующие утверждения:

1°. Функционал 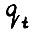положительно однороден, вогнут и монотонен (т.е. x > y влечет 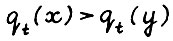) для любого t = 0,1,... .

2°. Для всякого 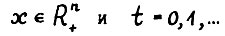имеет место равенство

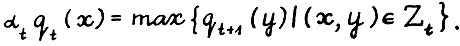
(1.12)

3°. 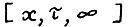- траектория 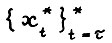- является оптимальной тогда и только тогда, когда выполняется

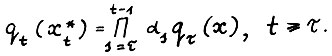
(1.13)

4°. Рассмотрим компактное множество 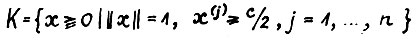, где c - константа из А.1.5, и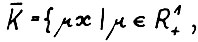 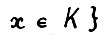- его коническую оболочку в 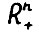с вершиной в нуле. Тогда функционалы 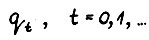являются равностепенно лишпицевыгли на 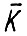, т.е. существует константа L > 0, такая что для любых 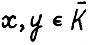выполняется 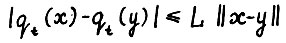для всех t = 0,1,....

Из теоремы, в частности, следует, что эффективная последовательность функционалов является нелинейной характеристикой оптимальных траекторий модели(см. /10/),не зависящей от её начального состояния, и тем самым любая бесконечная оптимальная траектория может быть построена путём последовательного решения в каадый период времени одношаговой задачи условной максимизации соответствуюцего эффективного функционала вида (1.12). В общем случае, чтобы найти эффективные функционалы, нужно, в свою очередь, уметь строить бесконечные оптимальные траектории, однако, далее будет показано, что скользящий план с достаточно большим горизонтом Т₀ обеспечивает на каждом шахе приближённое решение указанной задачи условной максимизации.

Примечание. Рассмотрим модель 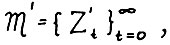где 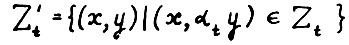. Она эквивалентна модели 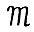в том смысле, что между траекториями этих моделей можно установить взаимнооднозначное соответствие,переводящее оптимальные траектории модели 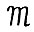в оптимальные же траектории модели 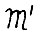(и наоборот). А именно, траектории 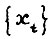модели 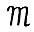ставится в соответствие траектория 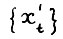модели 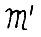, где 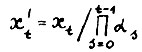. Легко видеть, что строго равновесной системе модели 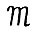соответствует также строго равновесная система модели 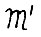, где темпы роста 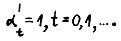. Приведённое рассуждение даёт право далее в доказательствах всех утверждений (§§ 1.2 - 1.4) для простоты с сохранением общности считать, что α_t = 1 для t = 0,1,... .