Основные определения

Замкнутую динамическую модель производства в самом общем виде, предложенном впервые Д.Гейлом /4/, можно определить с помощью последовательности технологических множеств

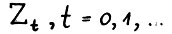
, лежащих в прямом произведении 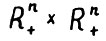и состоящих из пар (х, y), называемых допустимыми технологическими процессами, n - мерные векторы x и y описывают состояния экономики, соответственно, в начале периода t и к началу следующего периода t+1: их компоненты обозначают объёмы различных продуктов (в широком смысле, включающем сырьё, услуги, трудовые и природные ресурсы, фонды и т.д.), имеющиеся в данный момент времени в системе. Принадлежность пары (x, y) множеству Z_t означает, что если к началу периода t система находится в состоянии x, то технологически возможен её переход в течение этого периода в состояние y.

В описанной форде могут быть представлены, например, общеизвестные модели Неймана и Леонтьева (см. /11/).Так, для модели Неймана с неотрицательными матрицами затрат и выпуска A и B, соответственно, одинаковой размерности n*m, технологические множества имеют вид

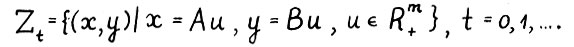
Если задан вектор состояния системы в некоторый начальный момент времени, то в терминах допустимых технологических процессов можно описать всевозможные варианты её развития во времени:

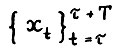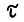Определение 1. Последовательность , где - любое натуральное, Т - натуральное, либо равно +∞, 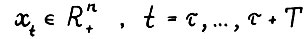, называется допустимой 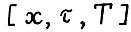- траекторией, есл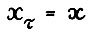и и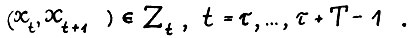

Поскольку допустимая 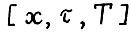- траектория, вообще говоря, не единственна, то необходимо ввести принцип определения наилучших вариантов из множества таких траекторий.

Определение 2. Допустимая 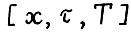- траектория 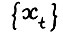, где 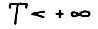называется оптимальной, если ни для какого числа λ > 1 не существует допустимой 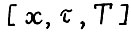- траектории 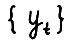, такой что 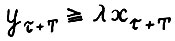, т.е. обеспечивающей в конце планового периода строго больший выпуск пропорционально по всем компонентам.

Пусть u - произвольная определённая на 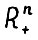монотонная функция, т.е. такая, что неравенство 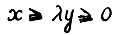для λ > 1 влечёт u(x) > u(y). Легко видеть, что класс траекторий, отвечающих определению 2, включает, в частности, траектории, максимизирующие величину 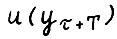на множестве допустимых 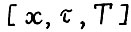- траекторий .

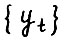Введём понятие бесконечной оптимальной траектории, исходя из условия согласованности, т.е. потребуем, чтобы отрезок любой длины этой траектории был оптимальной траекторией.

Определение 3. Допустимая 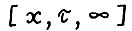- траектория 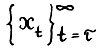,где τ - любое натуральное число, называется оптимальной, если каждый её конечный отрезок 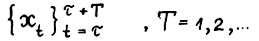оптимален в смысле определения 2 (иногда для определённости будем такую траекторию называть бесконечной оптимальной).

Таким же образом определяются бесконечные оптимальные траектории в/10, § 8. 7/.Там же при достаточно общих предположениях, которым, в частности, удовлетворяют рассматриваемые здесь модели, доказано, что для любого х ≥ 0 бесконечная оптимальная траектория существует.

Наконец, дадим точное определение основному понятию настоящей работы.

Определение 4. Последовательность 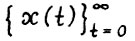называется скользящим планом с горизонтом 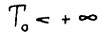, если для кавдого t = 0,1,... существует оптимальная 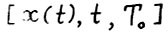- траектория 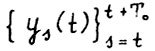(см. определение 2), такая что 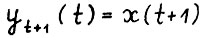. Здесь x(0) = y₀(0) - вектор начального состояния, y_s(t) - вектор плановых заданий, рассчитанный в момент t на s - t лет вперёд.