Список основных обозначений

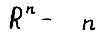  - мерное линейное пространство.

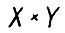  - прямое произведение пространств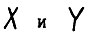

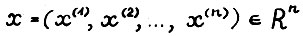  - вектор с координатами x^(j)

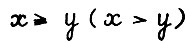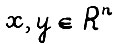 , где , означает, что 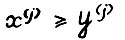(cоответственно,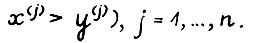

Аналогично, если 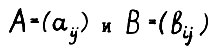- матрицы одинаковой размерности, то записи 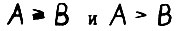(и в частности 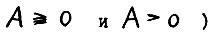означают выполнение для всех элементов неравенств 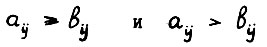, соответственно ( 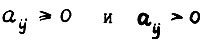соответственно).

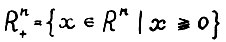  - неотрицательный ортант Rⁿ.

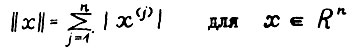 , где |а| - абсолютная величина числа a.

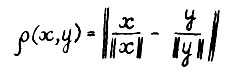  - угловое расстояние между ненулевыми векторами x и y.

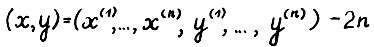  - мерный вектор, составленный из векторов :

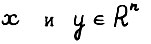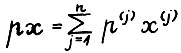  - скалярное произведение векторов 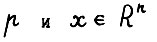(линейные функционалы в Rⁿ рассматриваются как векторы из Rⁿ).

Если а - скаляр, то ах - результат умножения вектора x на число a.

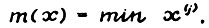
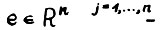  вектор, все координаты которого .

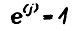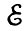  - матрица размерности n*n, все элементы которой равны 1.

Ax, где А - матрица размерности 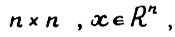понимается как умножение матрицы справа на вектор-столбец.

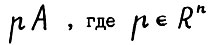  - как умножение матрицы слева на вектор-строку.

Т - знак транспонирования, так что если x рассматривается как вектор-столбец, то x^T - вектор-строка.

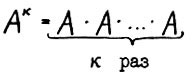  - к-я степень квадратной матрицы А.

Если к = 0, то А^к - единичная матрица.

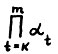  - произведение чисел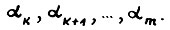

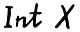  - внутренняя часть множества Х.

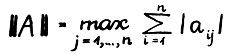  - норма матрицы А.