Развлечения. Игры

859. На листе бумаги или на классной доске записан "столбик" чисел:

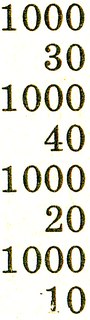
Все числа закрываются бумагой. Открывайте "столбик" число за числом, и пусть ваш товарищ быстро суммирует их устно и в конце назовет вам ответ. Верно ли сосчитал ваш товарищ? (Обычно многие называют ответ 5000, а на самом деле 4100.)

860. Не отрывая карандаша от бумаги и не проходя ни один из отрезков дважды, изобразите фигуру, как на рисунке 64.

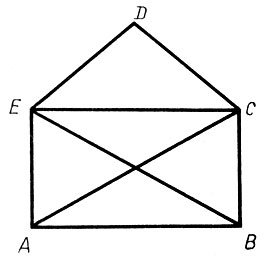
Рис.64

861. Угадайте задуманное число. Предложите своему товарищу задумать какое-либо трехзначное число и приписать к нему точно такое же число. Получившееся шестизначное число попросите умножить на 2, результат разделить сначала на 7, затем то, что получится, разделить на 11 и наконец разделить на 13. Если ваш товарищ скажет, что деление нацело не выполняется, то уверенно заявите, что товарищ ошибся, и предложите ему исправить ошибку. Спросите, какой получился ответ, и вы немедленно назовете задуманное товарищем число, разделив названный ответ на 2.

Подумайте, почему так получается. Вместо того чтобы умножать получающееся шестизначное число на 2, можно предложить умножить его на 3, 5, 10 и другие числа. Тогда для получения задуманного числа названное товарищем число придется делить соответственно на 3, 5, 10 и т. д.

862. Угадайте, сколько получится. Предложите своим товарищам: "Задумайте каждый какое-либо трехзначное число, но обязательно такое, чтобы цифра сотен отличалась от цифры единиц и не была бы на единицу меньше или больше ее. Напишите для задуманного числа обращенное, т. е. число, изображенное теми же цифрами, но взятыми в обратном порядке. Из этих двух чисел (задуманного и обращенного) возьмите большее и вычтите из него меньшее. Для получившейся разности напишите снова обращенное число и вычислите сумму этой разности и обращенного для нее числа".

Когда все это будет сделано, предложите одному из своих товарищей к получившемуся у него числу прибавить 100, другому - 200, третьему - 300 и т. д.

Вы можете каждому из участвующих в игре сказать, какое именно число у него получилось. Для этого вам каждый раз нужно будет прибавлять к числу 1089 то число, которое вы просили прибавить в конце. Тдк, у первого должно получиться 1189, у второго 1289 и т. д.

Еще лучше будет, если вы эти числа заранее напишете на листочках бумаги, вложите эти листочки в конверты и на них напишете имена своих товарищей, участвующих в этой игре. Вам останется торжественно вручить эти конверты их адресатам. Постарайтесь понять, в чем тут дело, и потом объясните своим товарищам.

863. Делимость на 11. Предложите товарищу написать на классной доске или бумаге любое многозначное число. К этому числу вы можете быстро приписать справа или слева одну цифру так, чтобы получившееся число разделилось на 11. Если, например, ваш товарищ напишет число 43 572, то вам нужно будет приписать справа или слева к этому числу 1. Получившееся число разделится на 11.

Знаете ли вы, какую цифру нужно приписать к числу, чтобы получившееся после этого число делилось на 11? Чтобы разобраться в этом вопросе, воспользуйтесь признаком делимости на 11: на 11 делятся те и только те числа, у которых сумма цифр, стоящих на нечетных местах, либо равна сумме цифр, занимающих четные места, либо больше или меньше ее на число, делящееся на 11.

Прежде чем выступать с этим числовым фокусом, поупражняйтесь, а потом объясните его вашим товарищам.

864. Угадайте задуманное число. В своей книге "Арифметика" Леонтий Филиппович Магницкий привел следующий способ отгадывания задуманного двузначного числа: "Если кто задумает двузначное число, то ты скажи ему, чтобы он увеличил число десятков задуманного числа в 2 раза, к произведению прибавил бы 5 единиц, полученную сумму увеличил в 5 раз и к новому произведению прибавил сумму 10 единиц и числа единиц задуманного числа, а результат произведенных действий сообщил бы тебе. Если ты из указанного тебе результата вычтешь 35, то узнаешь задуманное число". Почему так получается?

865. Угадайте сумму цифр задуманного числа. Предложите своим товарищам каждому задумать какое-нибудь трехзначное число, запись которого не содержит одинаковых цифр. Пусть затем, беря цифры задуманного числа по две, каждый составит всевозможные двузначные числа (таких чисел будет 6) и вычислит сумму всех этих чисел. Спросите у любого участника этого развлечения, какая сумма получилась. Разделите ее на 22, и вы найдете сумму цифр задуманного твоим товарищем числа.

Пусть, например, твой товарищ задумал число 145. Сумма всех двузначных чисел для этого числа будет равна 14 + 15 + 45 + 41 + 51 + 54 = 220. Если вы разделите эту сумму на 22, то действительно получите 10 - сумму цифр задуманного числа. Почему так получается?

866. Угадайте зачеркнутую цифру. Известен арифметический фокус. Состоит он в следующем. Предлагается написать любое трехзначное или четырехзначное число, состоящее из различных цифр. Какое именно число будет написано, отгадывающий не должен знать. Написавший число имеет право как угодно переставить цифры этого числа. Получатся два числа: записанное вначале и получившееся из него после перестановки цифр. Меньшее из этих чисел предлагается вычесть из большего, в полученной разности зачеркнуть одну цифру и вычислить сумму оставшихся. Эта сумма сообщается отгадывающему, и он говорит, какая цифра была вычеркнута.

Чтобы узнать, какая цифра была вычеркнута, отгадывающий поступает так: названную ему сумму цифр он дополняет до ближайшего большего кратного 9 (9, 18, 27, 36 и т. д.). Дополняющее число и дает вычеркнутую цифру. Если сумма сама окажется кратной 9, то зачеркнутая цифра была 0 или 9. Объясните этот фокус.

867. Мгновенное суммирование. Пусть кто-нибудь из ваших товарищей молча запишет на доске разность двух чисел. Вычислять разность не нужно. Тот, кто записал первую разность, или другой должен будет далее написать новую разность так, чтобы вычитаемым во второй разности было уменьшаемое первой разности. Производить вычисления также не нужно. Затем записывается третья разность так, чтобы вычитаемое было равно уменьшаемому второй разности. Продолжая, можно записать на доске любое число таких разностей. Пока это делается, вам на доску смотреть не следует. Как только все разности будут записаны на доску, повернитесь к ней лицом, посмотрите на записи, и вы сразу же можете сказать, чему будет равна сумма всех записанных, но не вычисленных разностей. Для этого вам нужно будет из уменьшаемого последней разности вычесть вычитаемое первой разности. Пусть, например, на доске будут записаны такие разности: 340-80; 450-340: 620 - 450; 680 - 620; 700 - 680; 825 - 700; 900 - 825. Сумма всех этих разностей будет равна 900 - 80, т. е. 820. Пусть ваши товарищи проверят вас, вычислив каждую разность, а затем и сумму их. Конечно, можно записывать разности не только целых чисел, но обыкновенных и десятичных дробей, а также положительных и отрицательных чисел.

Почему так получилось? Разберитесь сами и объясните товарищам.

868. Удивительная память. Запишите заранее на классной доске или на листе бумаги 30 - 50, а можно и больше, многозначных чисел. При записи чисел нумеруйте их. Эти числа записывайте так. К номеру числа прибавьте 9, возьмите для получившегося числа обращенное. Это будет число миллионов. Дальше вычислите сумму цифр получившегося числа миллионов. Число единиц (только единиц) этой суммы даст число сотен тысяч. Чтобы найти число десятков тысяч, вычислите сумму двух последних цифр, т.е. числа миллионов и числа сотен тысяч, и возьмите опять только единицы этой суммы. Так же продолжайте дальше. Вот несколько примеров таких чисел, какие вы запишите. № 5 41561785; № 11 2246066; № 16 52796516. Подготовив все это, вы можете удивить своих товарищей замечательной памятью. Отвернитесь от доски и скажите товарищам, что вы запомнили все эти числа. Вам не поверят. Тогда предложите им проверить. Пусть кто-нибудь скажет вам номер числа. Вы, производя устно вычисления, будете читать число, как бы медленно вспоминая его. Делайте это так. Пусть вам назовут номер числа 32. Молча вычисляйте: 32 + 9 = 41, обращенное число 14, говорите: 14 миллионов. 1 + 4 = 5 - пятьсот, 4 + 5 = 9 - девяносто, 5 + 9 = 14 - 4 тысячи, 9 + 4 = 13 - триста, 4 + 3 = 7 - семьдесят, 7 + 3 = 10 - единиц (14594370).

869. Угадайте возраст и дату рождения. Пообещайте своим товарищам угадать возраст и дату рождения каждого из них. Для этого заставьте каждого из них проделать следующие вычисления. Порядковый номер месяца рождения нужно умножить на 100 и к получившемуся произведению прибавить число месяца, на которое приходится день рождения. Затем полученную сумму нужно умножить на 2 и к тому, что получится, прибавить 8. Результат нужно умножить на 5, к произведению прибавить 4 и получившуюся сумму умножить на 10. К тому, что получится, остается прибавить полное число лет (возраст), увеличенное на 4. Пусть каждый, выполнивший все эти вычисления, запишет на листочке бумаги свою фамилию, получившееся число и передаст листочек вам. Получив эти листочки, вы по ним каждому можете сказать его возраст и дату рождения. Придется поступать так: из получившегося числа, записанного на листочке, каждый раз вычитайте по 444 и разность разбивайте на грани справа налево по две цифры в каждой. Первая грань справа даст возраст, вторая - число и третья - порядковый номер месяца рождения.

Разберитесь в "секрете" этого развлечения и объясните его товарищам.

870. Угадайте задуманное число. Приготовьте семь карточек. На первой из них напишите все числа, начиная от 1 до 100, через одно число, т. е. 1, 3, 5, 7, 9, ..., 99. На второй карточке напишите числа: 2, 3, 6, 7, 10, 11, 14, 15, 18, 19, ..., 98, 99. На третьей числа: 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23, 28, ..., 92, 93, 94, 95. На четвертой- 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27, ..., 88, 89, 90, 91, 92, 93, 94, 95. На пятой сначала напишите 16 последовательных натуральных чисел, начиная с 16, следующие 16 последовательных чисел, начиная с 32, не записывайте, затем запишите снова 16 чисел, начиная с 48, и т. д. На шестой сначала запишите 32 последовательных натуральных числа, начиная с 32, следующие 32 числа не записывайте и наконец припишите следующие числа с 96 до 100. На последующей карточке запишите все натуральные числа, начиная с 64 до 100.

Дайте вашему товарищу приготовленные таким образом карточки. Пусть он задумает какое-либо число от 1 до 100, выберет карточки, на которых это число записано. Только взглянув на эти карточки, вы можете угадать задуманное число. Для этого нужно найти сумму первых чисел, записанных на выбранных карточках. (Числа на карточках можно располагать в произвольном порядке, только нужно запомнить, какие места занимают первые числа: 1, 2, 4, 8, 16, 32, 64.) Постарайтесь понять, почему так происходит.

871. Любимая цифра. Спросите у ваших товарищей, кто какую цифру любит. Пусть один из них назовет вам цифру 4. Предложите ему 4 умножить на 9, а затем на получившееся произведение умножить число 12 345 679. В результате у него получится число 444 444 444, т. е. число, записанное с помощью только любимой им цифры. Если кто-нибудь скажет, что он любит 8, то предложите ему 8 умножить на 9, а затем умножить число 12 345 679 на получившееся произведение 72. У него получится число, записанное с помощью лишь любимой им цифры 8. Если же кто-нибудь назовет вам 0, то скажите, что О, конечно, очень важная цифра, но лично вы ее недолюбливаете, и попросите назвать другую цифру.

Постарайтесь разгадать "секрет" этого развлечения и объясните его вашим товарищам.

872. Как я узнаю? Номер дома, в котором вы живете, умножьте на 4, к результату прибавьте 7, полученное число умножьте на 25, прибавьте к полученному произведению свой возраст (целое число ваших лет) и число 125. Скажите мне, какое у вас получилось число, и я назову вам номер дома, в котором вы живете, и сколько вам лет. Как я все это узнаю?

873. Сколько братьев и сколько сестер? Вы можете узнать, сколько братьев и сколько сестер у вашего товарища. Пусть он прибавит к числу братьев 3, полученное число умножит на 5, к полученному произведению прибавит 20, сумму умножит на 2, прибавит число сестер и еще 5. По названному результату этих вычислений вы можете легко установить, сколько братьев и сестер у вашего товарища. Как вам это сделать?

874. Угадайте задуманный час. Воспользуйтесь картонной моделью циферблата часов. Пусть ваш товарищ задумает, который час (1, 2, 3, ..., 12). Объясните, что вы указкой будете показывать числа на циферблате. Каждый раз ваш товарищ должен прибавлять сначала к задуманному им часу единицу, затем к получившейся сумме единицу и так далее. Когда у него получится 20, он должен сказать "стоп". В этот момент ваша указка должна показать задуманный товарищем час. Чтобы это случилось, поступайте так. Первые 7 раз показывайте какие угодно числа на циферблате часов. В восьмой раз покажите 12, а дальше показывайте по порядку 11, 10, 9 и так далее. Найдите объяснение.

875. Быстрое извлечение кубического корня. Пусть ваш товарищ возведет в куб какое-нибудь двузначное число и сообщит вам результат. Вы можете быстро узнать, какое именно число возводилось в куб (извлечь кубический корень). Для этого вам понадобится таблица кубов однозначных чисел: 1³ = 1, 2³ = 8, 3³ = 27, 4³ = 64, 5³ = 125, 6³ = 216, 7³ = 343, 8³ = 512, 9³ = 729. Вам достаточно запомнить цифровое окончание каждого из правых чисел и соответствующее основание куба. Поступайте так. Названное вам число мысленно разделите на грани по 3 знака справа налево (левая грань может содержать и меньше трех знаков). По окончанию правой грани вы легко найдете цифру единиц искомого кубического корня. Цифра десятков корня находится по левой грани, с помощью таблицы кубов однозначных чисел. Приведем пример. Пусть товарищ назовет вам число 571 787. Последняя цифра этого числа 7, следовательно, число единиц корня 3. Левая грань у нас 571, но число 571 заключено между числами нашей таблицы кубов 512 и 729, поэтому десятков в искомом корне 8. Товарищ возвел в куб число 83.

Прежде чем показывать свое умение извлекать кубические корни, потренируйтесь.

876. Сравнение кривой и прямой. Подготовьте две деревянные планочки (рис. 65), полоску бумаги и масштабную линейку. Покажите первую планочку своим товарищам и предложите на глаз сравнить длины двух прямолинейных краев ее. Задайте вопрос: на сколько сантиметров АВ длиннее CD? Ответы запишите на доске, а затем предложите отвечающему произвести измерения. Обычно два отрезка прямой линии (тем более параллельные) сравниваются довольно точно. После этого покажите вторую планочку и спросите, на сколько сантиметров прямолинейный край ее АВ короче криволинейного края CD. Обычно близких к действительности ответов не бывает. Допускаются грубые ошибки. Покажите это, "воспользовавшись полоской бумаги и масштабной линейкой.

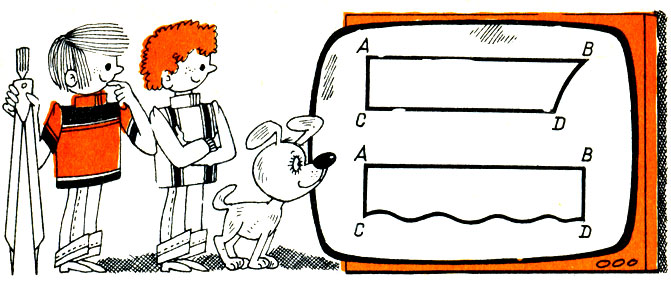
Рис.65

877. Угадайте. Сделайте из картона два круга, как показано на рисунке 66. Радиус большего круга пусть будет 20 см, а меньшего - 8 см. Меньший круг наложите на больший и скрепите их так, чтобы меньший круг мог поворачиваться вокруг общего центра их. С помощью двух этих скрепленных кругов вы можете отгадать, какого писателя задумает ваш товарищ.

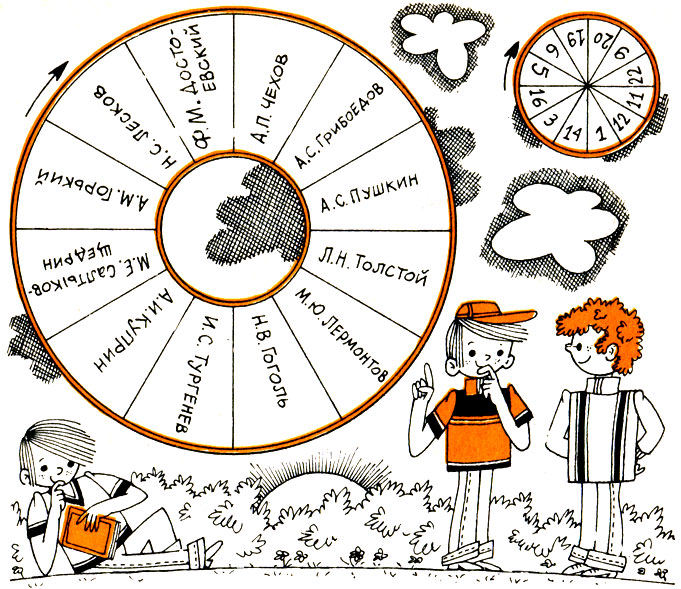
Рис.66

Делается это так. Товарищ должен задумать одного из писателей, фамилии которых записаны в секторах большего круга; затем посмотреть, какое число стоит против этой фамилии на меньшем круге, и повернуть меньший круг в направлении, указанном стрелкой, на столько делений (частичных секторов), каково это число. Какое положение занимает вначале меньший круг - безразлично. На сколько делений повернет ваш товарищ меньший круг, вам также не нужно знать.

Чтобы угадать задуманного писателя, вам достаточно будет взглянуть, какое положение займет меньший круг. Против фамилии задуманного писателя будет стоять всегда число 12. Постарайтесь разгадать "секрет" этих удивительных кругов.

Вот еще один вариант таких кругов: с их помощью вы можете узнать, какие виды спорта любят ваши товарищи.

Математическая шкатулка