Ответы и указания к решению задач

8. 2. Указание. Искомое число равно ^{102 +112 + 122}/₃₆₅ + ^{132 + 142}/₃₆₅ = 1 + 1 = 2. 9. 1) Перепишите сумму в таком виде: (1 - ¹/₂) + (¹/₂ - ¹/₃) + (¹/₃ - ¹/₄) +...+ (¹/₉ - ¹/₁₀) = ⁹/₁₀. 10. 1) Частное равно 2*3*4*6 = 144, остаток равен 1. 2) 1. 11. Рисунок 67.

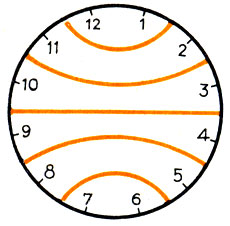
Рис.67

12. Например: 1) (⁵/₅)⁵; 2) (5 - 5)⁵; 3) (5 + 5)*5; 4)(5*5):5. 13. Например: 22 + 2 + 2 + 2. 14. Например: ²²²/₂. 15. например: 1) 99 + ⁹/₉; 2) 99 + ⁹⁹/₉₉; 16. Например: 1) 33 - 3 + ³/₃; 2) 3*3*3 + 3 + ³/₃; 3) 5*5 + 5 + ⁵/₅. 17. Например: 1) 111 - 11; 2) 33*3 + ³/₃ 3) (5 + 5 + 5 + 5)*5. 18. 123 - 45 - 67 + 89. 19.^{4 + 4}/_{4 + 4}; ⁴/₄ + ⁴/₄; ^{4 + 4 + 4}/₄; ^{4 + (4 - 4)*4}; ^{4*4 + 4}/₄; ^{4 + 4}/₄ + 4; 4 + 4 - ⁴/₄; ^{(4 + 4)*4}/₄; 4 + 4 + ⁴/₄; 4 + 4 + 4 - √4. 20. Например: 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8*9. 21. Например: 2 + 2 + 2 + 2 + 2 + 2 - 2 - 2. 22. 5 + ^{5 + 5 + 5}/₅; 5*^{5*5 - 5}/₅. 23. 1) 1 + 2 + 34 + 56 + 7; 2) 9 + 8 + 7 + 65 + 4 + 3 + 2 + 1. 24. 0. 25. а) 2 + 2 = 2*2; б) n и 1; n + 1 > n*1. 26. а) 36; б) 600. 27. 10²⁰ = 10¹⁰*10¹⁰ > 10¹⁰*2¹⁰. 28. 100²⁰ = 100¹⁰*100¹⁰ > 90¹⁰*100¹⁰ = 9000¹⁰. 29. 35. 30. 1)111; 2)11¹¹. 31. 2 - ²/₂. 32. (-9)⁹. 33. 1, 4, 5, 6, 9; 1, 2, 3, 4, 5, 6, 7, 8, 9; 1, 5, 6. 34. Нет. 35. 3³³, 4⁽⁴⁴⁾. 36. 9⁽⁹⁹⁾ - это число - великан среди чисел. Для обычной записи его требуется 369693100 цифр. 37. a^{n - 1}, где a^{n - 1} ∈ N; неверно говорить о дробном или отрицательном числе раз. 38. Бачок емкостью 20 л. 39. Каждый должен получить ⁵/₆ яблока, но ⁵/₆ = ¹/₂ + ¹/₃. 3 яблока нужно разрезать пополам и 2 яблока - каждое на три равные части. 40.⁷/₁₂ = ¹/₃ + ¹/₄. 41. 59. Если к искомому числу прибавить 1, то оно будет делиться без остатка на 2, на 3, на 4, на 5, на 6. Наименьшее такое число 2*3*2*5 = 60. Искомое число 59. 78. 5 ч. 79. Пионеры ехали на автомашине в 12 раз быстрее, чем шли пешком. 80. 2 кг. 81. Пирожное стоит 22 к., пирожок - 9 к. 82. I - 270 т; II - 130 т; III - 170 т. 83. У старшего 5 р. 60 к., у младшего 4 р. 84. 12 и 4. 85. 12 ^км/_ч. 86. 7 слив. 87. 8 кг. 88.¹/₁₂. 89. 13 ч 20 мин. 90. Через 7 лет. 91. 51 и 17. 92. 2 ⁸/₁₁ м и 2 ⁸/₁₁ дм. 93. 60 и 40 билетов. 94. 15 пакетов по 3 кг и 9 пакетов по 5 кг. 95. 3 кг. 96. Через 4 мин. 97. 16 км. Указание. Второй догонит первого через 2 ч. За это время собака пробежит путь, равный 16 км. 98. Через 15 мин. 103. Длина поезда 225 м, скорость его 54 ^км/_ч. 104. 400 км, 40 ^км/_ч. 105. 4 ч 30 мин. 106. 50 мин. 107. I - 46 ¹/₃ аршина; II - 34 ¹/₃ аршина; III - 25 ¹/₃ аршина. 108. 36 гусей. 109. 28 учеников. 110. 38 ¹⁴/₄₇ р. 111. Кроликов - 12, фазанов - 23. 112. За 12 ч; I - 30 четвертей; II - 27 четвертей; III - 24 четверти. 113. За ⁶/₁₁ ч. Указание. За 6 ч первая труба наполнит 6 таких водоемов, вторая - 3, а третья - 2, всего 11 водоемов. Значит, три трубы вместе наполнят один водоем за ⁶/₁₁ ч. 114. За 24 ч. 115. За 35 дней. 116. За 12 ч вол съест 12 копен, конь - 6, коза - 4, всего 22 копны. Поэтому одну копну вол, конь и коза вмёсте съедят за ⁶/₁₁ ч. 117. За 12 лет четыре плотника вместе могут построить 25 дворов, а один двор они построят за ^365*12/₂₅, т.е. за 175 ¹/₅ дня. 118. 9 ⁷/₃₇ дня. 119. За 15 мин. 120. По 285 верст. 121. В 8 дней. 122. 12,5. 123. 7 дынь. 124. 9, 4, 2 и 1. 125. 255. 126. 27. 127. 79. 128. 21 к. 129. 29 дней. 130. 59 мин. 131. Можно. Сначала нужно отлить 2 л в трехлитровый сосуд. Какими должны быть дальнейшие переливания, сообразить не трудно. 132. Сначала в третий сосуд нужно из первого отлить 3 л. Дальнейшее просто. 133. Сначала из первого сосуда следует отлить во второй 7 л, затем из второго 2 л в третий. 134. Следует в сосуд, емкость которого 4 л, набрать 1 л жидкости. Последующее не составляет труда. 136. Сообразите, как набрать в девятилитровый сосуд 8 л воды. 136. Позаботьтесь о том, чтобы в одном сосуде оказался 1 л воды. 137. Из сосуда в 12 л можно налить в девятилитровый сосуд любое натуральное число литров жидкости от 1 до 9, а в пятилитровый - от 1 до 5. 138. Надо наполнить 8-пинтовый сосуд, вылить из него 5 пинт в другой сосуд, а оставшиеся 3 пинты перелить в 5-пинтовый сосуд. Второй раз наполнить 8-пинтовый сосуд и отлить из него 2 пинты в 5-пинтовый сосуд. В 8-пинтовом сосуде останется 6 пинт. 139. 1) 11 ¹/₉(33 ¹/₃% - это ¹/₃); 2) 100; 3) 4,25 (вычислить 17% от 25 - это то же, что вычислить 25% от 17); 4) 9 (можно заменить вычислением 12,5% от 72, а 12,5% равно ¹/₈). 140. 67%. 141. 31,5%. 142. На 32%. 143. Товар подешевел на 1%. 144. На 50%. 145. На 28,6%. 146. На 25%. 147. На 33 ¹/₃%. 148. 83,6%, 16,4%. 149. Второй. Указание. Скорость первого рабочего равна ⁹/₁₀*¹¹/₁₀ = ⁹⁹/₁₀₀ cкорости второго. 150. На 21%. 151. На 32%. 152. Уменьшится на 9%. 153. На 72,8%, на 44%. 154. На 8,9%. 155. 441 г. 156. 12 345 679*24 = 296 296 296. 157. 1) 37*21 = 777 или 15*37 = 555; 2) 256*13 = 3328; 3) 37*99 = 3663; 4) 209*209 = 43 681; 5) 153*153 = 23 409; 6) 5291*189 = 999 999. 158. 1) 6 + 67 + 674 = 747; 2) 342 457 + 342 457 = 684 914; 3) 364 768 + 364 768 = 729 536; 4) 2222*222 = 493 284; 5) 3125:25 = 125; 6) 198; 7) 4 748 253. 159. 9382 + 3152 = 12 534. 160. 1) 90 909 + 10 101 = 101 010; 2) 769 - 504 = 265; 3) 769 + 504 = 1273; 4) 10 652 - 9067 = 1585; 5) 87 130 + 8213 = 95 343. 161.

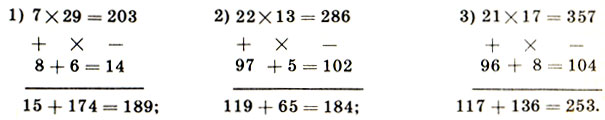
162. 1) 3328:13 = 256; 2) 19 275:75 = 257; 3) 15 625:25 = 625. 163. 1) 6750 - 3894; 2) 44,45 + 59,27 + 78,43; 3) 27*32; 4) 66*111; 5) 324*57; 6) 568*24; 7) 315*41; 8) 40,5*2,07; 9) 48 384:126; 10) 52 650:325; 11) 1089 700:12; 12) 110 768:112. 164.¹/₂. 165. Когда делитель равен 1. 166. Делится на 7, 11 и 13. 167. 1 001 001. 168. Сумма двух последовательных чисел может быть простым числом, в остальных случаях - составное число. 169. 2 - простое четное число. 170. 3. 171. а) 6; б) 3; в) 3. 172. Не делится. 173. 4. 174. 2. 175. 100. 176. |а| < 2, или а² < 4. 177. 1. 178. 0,0001 га. 179. 70 км, если велосипедисты ехали по прямолинейной дороге. 180. 297 м. 181. На 20 тетрадей. 182. 90 к. 183. 2. 184. 90 ступеней. 185. 3,5 л. 186. На 4 ^км/_ч. 187. 3a 2,4 мин. 188. He менее одной (мотоцикл двигался в поселок). 189. Задачу можно истолковать так: дед, отец, сын: всего 3 человека. 190. Велосипедисты встретятся на одном и том же расстоянии от A. 191. Иногда обыкновенной дробью выражают нумерацию углового дома квартала (числитель - номер этого дома по одной улице, знаменатель - номер его по другой улице). Такую дробь сокращать нельзя. 192. 6. 193. 10,5 к. и 0,5 к. 194. 11 с. 195. 36; 24. 196. 0. 197. 0. 198. Все эти равенства можно истолковать на "языке" часов. 199. 4 (или немного больше). 200. Например: первому дать 2 яблока, второму - 1 и третьему - 1. 201. 1,5. 202. 3*45 = 135, или 3*40 + 5 = 125. 226. Рисунок 68.

Рис.68

227. Рисунок 69.

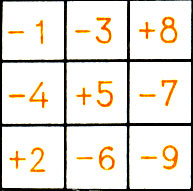
Рис.69

229. 1) a = 0, b ≠ 0; 2) a = b; 3) a = -b; 4) a > b > 0 или a < b < 0; 5) 0 < a < b и b < a < 0. 230. Рисунок 70.

Рис.70

239. При основании 4. 240. Верно в cистеме счисления при основании 8. 241. 1) 34311₅; 2) 102220₃; 3) 1000000₂. 242. 1) 37; 2) 410; 3) 12 925; 4) 2594. 243. 1) В 6 раз; 2) в 216 раз. 244. 1) Уменьшится в 3 раза; 2) уменьшится в 27 раз. 245. 1) При основании 3; 2) при основании 6; 3) при основании 8. 246. 1) 3₁₀ = 3₈; 2) 14₁₀ > 14₈; 3) 111₂ < 111₈; 4) 0,11₂ > 0,11₁₀; 5) 0,21₁₀ < 0,21₈; 7) 0,2₈ > 0,1463₈; в случаях 6), 8), 9) дроби равны. 247. 1) 10100000₂; 2) 101011111₂; 3) 11113₅; 4) 1011001₂; 5) 12313₅; 6) 22117₈; 7) 16303₈; 8) 2222₃; 9) частное - 1101₃, остаток 22₃. 248. 1) При основании 5; 2) при основании 9. 249. 1) При основании 5; 2) при основании 8; 3) при основании 8; 4) при основании 7. 250. 5*5 = 31, основание системы счисления 8. 251. Будет. 252. В разных системах счисления признаки делимости чисел, вообще говоря, различны. 253. 1) 1000₂; 2) 0,11₂; 3) 0,10011001100...₂; 4) 0,12₃; 5) 0,202020...₃. 254.⁷/₁₆ = 0,0111₂;¹/₃ = 0,010101...₂; ⁴/₅ = 0,11001100...₂. 255.⁴/₂₇ = 0,11₃, ⁴/₅ = 0,21012101...₃. 258. 15 лет, 7-й класс. 259. Наиболее экономична - троичная система (2³⁰ < З²⁰; З²⁰ > 4¹⁵:4⁵ > 10⁶). 260. 2) Цифры 0, 1, 2, базис - числа 1, 2, 5, 10, 20, 50, 100; 3) 1011011, 1121120, 111101; 4) 210 г, 26 г, 165 г. 261. 1) Цифры 0, 1, 2, 3, 4; базис - все заданные достоинства монет; 2) 2232001, 20001100, 10100010; 3) 94 к., 56 к., 90 к. 262. 1) Цифрами первых двух разрядов служат натуральные числа от 0 до 59, третьего - от 0 до 23, четвертого - от 0 до 30; пятого - от 0 до 11, шестого - от 0 до 99, седьмого - 0 и элементы множества натуральных чисел. 265. 88 + 8 + 8 + 8 + 888. 269. Через 6 дней. 270. 1-е взвешивание - 4,5 и 4,5 кг крупы; 2-е - 2,25 г и 2,25 кг; 3-е - 2 кг крупы и гирь на 250 г на одной чашке, на другой - 2,25 кг крупы. Возможны и другие решения. 371. В первый и во второй магазины следует завезти 3 полные бочки, 1 заполненную наполовину и 3 пустых, остальные бочки - в третий магазин. 272. 45. 273. Не делится. 274. 8а(а =0, 1, 2, ..., 6). 275. Не может. Указание. Если бы сумма 1 + 2 + 3+...+ k = ^{k(k + 1)}/₂ оканчивалась цифрой 7, то k(k + 1) оканчивалась бы цифрой 4. Но k(k + 1) может оканчиваться лишь цифрами 0, 2 и 6. 276. Остаток 5. 277. Произведение двух натуральных чисел, сумма которых меньше 13, будет наибольшим, когда каждое из этих чисел равно 6. 278. Из четырех натуральных чисел, сумма которых нечетна, нечетными могут быть одно или три. Произведение в этих случаях будет четным числом. 279. Сумма цифр данного числа - 300 - делится на 3 и не делится на 9, поэтому само число делится на 3 и не делится на 9, т. е. не может быть квадратом натурального числа. 280. 901. 281. 3. 282. 21. 283. 2²²². 284. 9⁽⁹⁹⁾. 285. В ≤ 9*1984 = 17 856, т. е. В - не более чем пятизначное число. Поэтому С ≤ 9*5 = 45 и делится на 9 (так как на 9 делятся А и В). Возможные значения С - 9, 18, 27, 36 и 45. 286. 1 кг, 3 кг, 9 кг, 27 кг. 287. 61 981. 288. 504. 289. 8; 12; 5; 20. 290. 801. 291. 60 129. 292. 1) 45; 2) 81. 293. 1) ²²/₃₅ = ¹¹⁰/₁₇₅ > ¹¹⁰/₁₇₇; 2) ¹⁹⁸³/₁₉₈₄ < ¹⁹⁸⁴/₁₉₈₅. 297. 424. 298. 1794. 299. 1) (10 + 1)(2 + 1)= 33; 2)3*4*6 = 72.

302. Верны высказывания: 1); 2); 3); 4), 5 б) и в); неверны 4 а) и г), 5). 303. 1) ложно; 2) и 3) истинны. 307. Верны утверждения: 6), 7), 8), 10), 14), 16), 17); неверны: 1), 2), 3), 4), 5), 9), 11), 12), 13), 15). 309. 1), 3), 6), 8), 10), 12), 15) достаточно; 2), 5), 9), 11) необходимо, 4), 7), 13), 14), 16) необходимо и достаточно. 310. 1) Если в одной и той же или равных окружностях дуги, меньшие 180°, равны, то и стягивающие их хорды равны. 2) Если в одной и той же или в равных окружностях хорды, отличные от диаметра, равны, то и стягиваемые ими дуги, меньшие 180°, равны. 315. Верно. 316. Верны. 317. Верны. 318. Неверна. 319. Такие треугольники могут быть равными, но могут быть и неравными. 320. Неверно. 321. Противоположное и обратное утверждения неверны. 322. Например, "смежные углы равны" и "два несмежных угла не равны". 323. Например, "смежные углы равны" и "два равных угла смежные". 324. Произведение - четное число. 325. Неверно. 327. Сумма двух чисел - четное число; трех - нечетное. 329. Может получиться и верное равенство. 330. Если бы в каждом классе учились по одному ученику, то учеников было бы 12. На самом же деле их 13. Пришли к противоречию. 331,332. Задачи решаются аналогично предшествующей. 333. 3 яблока. 334. 1) 12; 2) 7. 338. Стоимость всей покупки должна делиться на 3, покупалось 9 тетрадей, 3 карандаша, а каждый блокнот стоил 6 к. Но 58 не делится на 3. 339. Четыре года тому назад всем членам семьи было на 15 лет меньше (73 - 58), а не на 16. Значит, самого младшего члена семьи (сына) еще не было. Следовательно, сыну сейчас 3 года, дочери 5 лет, матери 31 и отцу 34 года. 340. Первый. 341. Каждое из этих чисел не больше 10, (3024 < 10 000). Среди этих чисел нет 5 и 10. Поэтому искомыми числами могут быть 1, 2, 3, 4 или 6, 7, 8, 9. Условию удовлетворяют числа 6, 7, 8 и 9. 342. Гири по 2 г, 13 г, 19 г и 60 кг. 343. Нужно выдать 2 ящика по 16 кг и 4 ящика по 17 кг (16*2 + 17*4 = 100). 344. 4 деления: 1 см, 2 см, 6 см и 10 см. 345. Длина контура должна быть в 6 спичек, а ширина в 5 спичек. 316. Совет: на листе бумаги нарисуйте канал и бухту, вырежьте из картона "теплоходы" и передвигайте их. 347. 1) Можно поступить так: 4 яблока разрезать на половинки, 2 яблока - на четыре равные части и 1 яблоко - на 8 равных частей. 2) 3 яблока можно разрезать каждое на 4 равные части и 4 яблока каждое на 3 равные части. 348. Вначале оба мальчика переправляются на противоположный берег (В) и один из них остается на нем. Второй мальчик доставляет к колхозникам лодку и сам высаживается на берег (А). В лодку садится один колхозник и переправляется через реку. Мальчик, оставшийся на берегу В, приводит лодку к берегу А, сажает в нее второго мальчика, переправляется с ним на берег В и т. д. 350. Из одного куска проволоки изготовить каркасную модель куба нельзя. Придется припаять 3 ребра и спаять еще 2 вершины. 351. От шахматной доски отрезаны 2 черные или 2 белые клетки, так что черных и белых клеток осталось разное число. Кость домино покрывает одну черную и одну белую клетку. Поэтому заданное покрытие невозможно. 352. Надо отделить второй перевязкой бобы от риса так, чтобы, развязав потом одну перевязку, можно было высыпать бобы, оставив в мешке рис. 353. Измерить диагональ основания кирпича, построить прямоугольный треугольник (для построения прямого угла можно воспользоваться тем же кирпичом) с катетами, длины которых равны длинам измеренной диагонали и толщины кирпича. Останется измерить длину гипотенузы этого треугольника. 354. Объяснение может быть таким: "Перед уходом к приятелю я завел свои часы и заметил их показания. Вернувшись, я снова посмотрел на свои часы. Сравнив первое и второе их показания, я установил, сколько прошло времени, затем вычел время пребывания в квартире приятеля и разность разделил на 2. Дома я поставил свои часы так, чтобы их показание было равно сумме времени, показанного часами приятеля при моем уходе от него, и результата моих вычислений". 355. Ошибка была допущена завещателем. Он упустил из виду, что ¹/₂, ¹/₄, ¹/₅ в сумме составляют не 1, а ¹⁹/ ₂₀. 356. Букетики продавались одновременно по одинаковой, но меняющейся цене. Например, могло случиться так, что сначала в первом киоске продано 3, во втором - 5 и в третьем - 6 букетиков по 1 р. за букетик, а оставшиеся букетики продавались по 1 р. за 3 букетика. Тогда на каждый киоск приходится по 13 р. 357. Кузнец разъединил 3 звена одного обрывка цепи. Этими звеньями соединил затем оставшиеся 4 обрывка в одну цепь. 358. Каждое звено трехзвенного обрывка цепи следует разрезать и соединить этими звеньями оставшиеся 4 обрывка. 359. Нужно распилить третье звено. 360.^{60 + 60}/₅ *2 = 48, а не 50, расчет дежурного ошибочен. 361. Вожатый должен был точно указать, как пионеру-художнику поступить: нарисовать автопортрет или нет. 362. Коля рассуждал так: у Васи и Пети - красные квадратики. Значит, у меня может быть либо белый квадратик, либо красный. Если бы у меня был белый квадратик, то либо Петя, либо Вася быстро сообразил бы, что у него красный квадратик. Петя мог бы рассуждать так: у Коли белый квадратик, а у Васи красный, значит, у меня красный, так как если бы у меня был белый, то Вася сразу бы сказал, что у него красный, потому что белых квадратиков всего два. Так же мог бы рассуждать и Вася. Но они молчат. Значит, у меня не белый квадратик, а красный. 363. Требуемую развертку можно вырезать так, как показано на рисунке 71.

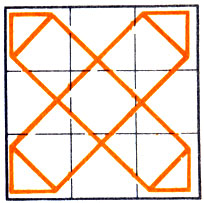
Рис.71

364. 5 учащихся. 365. 60%. 366. 20, 13, 30 и 20. 367. Не менее 10 детей. 368. Да, в отчете есть ошибки. 369. Возведение в квадрат денег не имеет смысла. В квадрат возводятся числа, а не величины. 370. Нельзя делить на 7 + 2 - 9 = 0. 371. Ошибка допущена в вынесении общего множителя за скобки в левой и правой частях тождества 4:4 = 5:5. 372. (4 - ⁹/₂)² = (5 - ⁹/₂)² ⇔ |4 - ⁹/₂| = |5 - ⁹/₂|. 373,374. Ошибка такого же вида, как и в задаче 372. 375. Из равенства квадратов двух чисел не следует, что сами эти числа равны. 376. Уравнения данной системы несовместны. 377, 378, 379. Ошибка, как и в задаче 372. Нельзя делить на а - b, так как а - b = 0. 381. 381. Нельзя делить на b - а - с, так как 6 - а - с = 0. 382. Ошибка, как и в задаче 372. 383. Свойство: если в пропорции предыдущий член первого отношения больше последующего, то и предыдущий член второго отношения больше своего последующего - может оказаться неверным, если некоторые члены пропорции отрицательны. 384. При делении обеих частей неравенства (а + b)(а - b) > 2b(а - b) на а - b знак неравенства может измениться на противоположный (если а - b < 0). 385. Нельзя делить на а - а = 0. 386. Ошибка, как и в задаче 372. 387. (1 - ³/₂)² = (2 - ³/₂)² следует не 1 - ³/₂ = 2 - ³/₂, a - 1 + ³/₂ = 2 - ³/₂. Всегда √а² = |а|. 388. Рассуждения опирались на ошибочный чертеж. В действительности полуокружности пересекаются со стороной АС в одной точке, т. е. BE совпадает с BD. 389. D ∈ OB. 390. D ∈ AB. 391. Случаи, рассмотренные в рассуждении, невозможны. Выполните чертеж с помощью циркуля и линейки. 392, 393, 394. Ошибочные чертежи. 395. Если сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники не обязаны быть равными. 396. Ошибочен чертеж. Точка пересечения прямой, определяемой биссектрисой BD и серединного перпендикуляра к катету АС, находится вне треугольника ABC. 397. Мы воспользовались недоказанным утверждением: "Сумма внутренних углов любого треугольника постоянна". 398. (1) и (4) части прямоугольника (отличного от квадрата) неплотно примыкают ко (2) и (3) частям его. Между ними образуется "щель" в виде вытянутого параллелограмма. Площадь этой щели как раз равна 1 квадратной единице. 399. Отрезок А₁B₁ имеет длину, превосходящую длину окружности меньшего круга, так как меньший круг покатится по прямой А₁В₁ со скольжением. 400. Нельзя делить на AE*DE - СЕ*BE, потому что эта разность равна 0. 401. Используя (1) и (2), можно доказать, что z = х (докажите!) и, следовательно, z - х = 0. Поэтому деление на z - х недопустимо. 402. Формула sin²α + cos²α = 1 выводится на основании теоремы Пифагора, и поэтому в рассуждении получается порочный круг. 403. Деление на √х - √y недопустимо, так как х = у, и поэтому √х - √у = 0. 404.

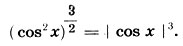
407. Верное решение у первого ученика. Второй ученик при возведении в квадрат обеих частей уравнения приобрел посторонний корень х = -6, поэтому его решение следует завершить проверкой корней. 408. Верно вычислял второй ученик. Ошибка первого ученика √(1 - n)² ≠ 1 - n, так как n = 3 > 1, то √(1 - n)² = 1 - n. 409.

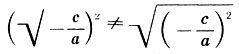
По определению квадратного корня,

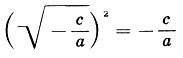
(при ^c/_a ≤ 0). 411. Рассуждение ошибочно. (Сравните с рассуждением: если стол дубовый, то он деревянный; этот стол не дубовый, следовательно, он не деревянный.) 412. Доказательство Вити верно только для найденного им способа построения. А если прямую, параллельную данной, построить иным способом? Совпадут ли построенные прямые? - вопрос остается открытым. 415. 3 мин. 416. Достаточно двух носильщиков. Первый из них должен возвратиться после первого дня пути, а второй - после второго, оставив себе необходимый запас пищи и воды, передав остальное оставшимся. 417. Если при первом измерении масса груза оказалась равной р г, а при втором - q г, то верная масса равна √pq . 418. Хозяйка отвесила более 2 кг. Пусть а - действительная масса крупы, отвешенной в первый раз, и b - во второй.По предшествующей задаче √ab = 1. Имеем:

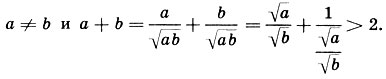
419. Перестановку шин нужно произвести через 9375 км пути. Грузовик без замены шин новыми пройдет всего 18 750 км. 420. Пусть х (км) - расстояние от школы до селения А, у (км) - до В и z (км) - до С. Все школьники за один раз пройдут 300х + 200у + 100z (км). Но 300х + 200у + 100z = 200(х + у) + 100(х + z). Учтем, что х + у ≥ |АВ|, х + z ≥ |АС|. Имеем: 300х + 200у + 100z ≥ 200. |АВ| + 100*|АС|. Сумма, стоящая в левой части неравенства, будет наименьшей при х + у = |AB| и x + z = |АС|, т. е. при условий

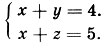
Это условие означает, что школу нужно построить в селении А. 421. (Рис. 72.)

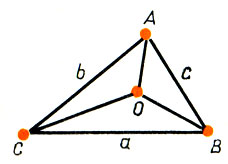
Рис.72

Возможны 6 маршрутов, длины которых равные, S₁ = ОА + с + а + СО; S₂ = OA + b + а + OB; S₃ = OB + a + b + OA; S₄ = OB + с + b + CO; S₅ = ОС + b + с; S₆ = OC + a + c + АО. Очевидно, что S₁ = S₆, S₂ = S₃, S₃ = S₄. Остается сравнить 3 маршрута: S₁, S₂ и S₄, что можно сделать графически (по рисунку, выполненному с помощью чертежных инструментов). 422. Порядок изготовления книг должен быть таким: B, А, С. Потребуется 10 ч. 423. Лента намотается спиралеобразно. Для расчетов, с достаточной для практики точностью, можно считать, что получается несколько концентрических цилиндрических слоев. При расчете длины каждого такого кольца можно исходить из длины средней окружности его. Тогда колец будет ^{130 - 30}/_2*0,25 = 200, диаметр средней окружности первого (наименьшего) кольца равен 30 + 2* ^0,25/₂ = 30,25 мм, диаметр средней окружности второго кольца будет 30,75 мм (увеличится на 0,5 мм) и так далее. Диаметр средней окружности последнего кольца 129,75 мм. Длины всех этих окружностей составляют арифметическую прогрессию: π*30,25; π*30,75; π*31,25; ...; π*129,25; π*129,75. Сумма их равна l = π*16 000 ≈ 50 250 (мм). Значит, лента должна иметь длину 50 м 25 см. 424. 25 ящиков по 40 деталей и 4 ящика по 25 деталей. 425. 25 путевок на 45 дней, 2 путевки на 27 дней и 20 путевок на 15 дней.

426. 176 экскурсантов. 427. 4 брата и 3 сестры. 428. 4 р. 80 к. 429. 48 км/ч. 430. 3 ветки и 4 галки. 431. 84 года. 432. 8 р., 12 р., 5 р. и 20 р. 433. 120. 434. 15. 435. 50 и 14 лет. 436. 18 лет. 437. Через 65 ⁵/11 мин. 438. Через 21 ⁹/₁₁ мин. 439. 1 ¹/₉ км. 440. 85 714. 441. 4. 442. Нужно из результата вычислений вычесть 4 и разность разделить на 2. 443. Результат вычислений (до деления на 10): 1000а + 100b + 10с; задуманное число 100а + 10b + с. 444. Мальчиков - 4, девочек - 6. 445. По условию составляется система двух уравнений с тремя переменными:

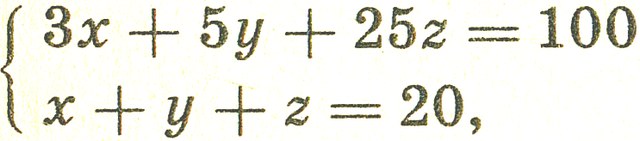
, где х - число денежных знаков по 3 р., у - по 5 р. и z - по 25 р. Исключив x, получим у + 11z = 20 ⇔ у = 20 - 11z. Но 0 ≤ у ≤ 20. Значит, z = 0 или z = 1. Имеем два решения: 1) х = 0, у = 20, z = 0 или 2) x = 10, у = 9, z = 1. 446. Задача имеет два решения: 1) 3 тетради по 7 к. и 8 по 4 к.; 2) 7 тетрадей по 7 к. и 1 тетрадь по 4 к. 447. Пешеход. 448. 5 девочек, 24 гриба. 449. 27 ^км/_ч. 450. ≈ 1800 км. 451. 80 см. 452. 1) 705,6 м; 2) ≈ 20,1 с. 453. 13. 455. 59%. 456. 20 коров. 457. 37. 482. 3) 7 ¹/₂*6 ¹/₂ = (7 + ¹/₂)(7 - ¹/₂) = 7² - (¹/₂)² = 48 ³/₄; 4) 143 ¹⁵/₁₆; 5) 98² - 4 = (98 - 2)(98 + 2) = 9600; 6) 2; 7) ¹⁰⁶/₄₇ - ₉₄/₅₃ = 2(⁵³/₄₇ - ⁴⁷/₅₃) = 2 ^{532 - 472}/_{(50 - 3)(50 + 3)} = ¹²⁰⁰/₂₄₉₁; 8) 199 + 195 + 191 +...+ 7 + 3 = (3 + 199)*25 = 5050 (сначала пользуемся тождеством а - b² = (а + b)(а - b)). 483. 1) -4; 2) 0; 3) 0; 4) 200. 484.Указание. Прежде сократите дробь. 3) Не существует. 485. 4аb. 486.³²/_{1 - a³²}. 489. 2²*3⁴ = 648. 490. √(S₁*S₂*S₃). 492. 16 807 мер. 493. 20 971 р. 52 к. 494. 655 р. 35 к. 495. Такого числа не существует. 499. В безветренную погоду полет проходит быстрее. Указание. Пусть расстояние между Москвой и Киевом а (км), собственная скорость самолета v (^км/_ч), а скорость ветра u (^км/_ч). Время полета туда и обратно в безветренную погоду будет равнo ^2a/_v (ч), а при ветре ^a/_{v + u} + ^a/_{v - u} (ч). Нo ^2a/_v < ^a/_{v + u} + ^a/_{v - u} (докажите!). 500. 37,5 ^км/_ч. Указание. Обозначьте расстояние между городами через а (км). Туда и обратно автомобиль проедет за ^a/₅₀ + ^a/₃₀ (ч), его средняя корость

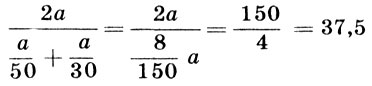
(^км/_ч). 501. 81¹⁰. Указание. Представить 80 = 81 - 1, а 82 = 81 + 1, затем раскрыть скобки и привести подобные члены. 502. х^x + х^{1 - x} = х + 1 ⇔ x^2x - хх^х + х - х^х = 0 ⇔ (х^х - 1)(х^х - х) = 0 ⇔ х = 1. 503. В V и VII классы. 504. 954. 505. (2n - 1)² = 2(2n² - 2n) + 1. 506. Само число не может быть нечетным, так как тогда квадрат его был бы нечетным числом (см. задачу 505). 507. (2n)² = 4n². 508. (n + 1)² - n² = 2n + 1. 509. (2n + 1)² - (2n - 1)² = 8n. 510. Числа: n - 1, n, n + 1. Сумма кубов их равна n³ - Зn² + Зn - 1 + n³ + n³ + Зn² + Зn + 1 = Зn(n² + 2). Докажем, что n(n² + 2) делится на 3. Имеем три возможности: 1) n = 3k; 2) n = 3k + 1; 3) n = 3k + 2. При первой возможности на 3 делится n; при второй - (Зk + 1)(9k² + 6k + 3) = (3k + 1)*3(3k² + 2k + 1); при третьей - (3k + 2)(9k² + 12k + 6)=(3k + 2)*3*(3k² + 4k + 2). 511. n(n + 1) + n +1 =(n + 1)². 512. 2n(2n + 2) = 4n(n + 1). Одно из чисел n или n + 1 четное. Поэтому 4n(n + 1) кратнo 8. 513. Пусть ab - двузначное число и а ≠ b. Тогда (10а + b) - (10b + а) = 9(а - b). В случае трехзначного числа соответствующая разность будет делиться на 99. 514. 1 + 3 + 5 + 7 +...+ (2n - 5) + (2n - 3) + (2n - 1) = 2n* ⁿ/₂ = n². 515. (10а + 5)² = 100а² + 100а + 25 = 100а(a + 1)+ 25; 35² = 1225; 55² = 3025; 125² = 15 625. 516. n(n + 1)(n + 2). Одно или даже два из этих чисел четные и одно обязательно кратно 3. 517. Первое из этих чисел четное, второе нечетное и третье четное. Одно из этих двух четных чисел делится на 4, другое - на 2. Кроме того, одно из трех последовательных натуральных чисел делится на 3. Произведение этих чисел делится на 2; 3; 4; 6; 8; 12; 24. 518. m³ - m = m(m + 1)(m - 1) = (m - 1)m(m + 1). Далее см. задачу 516. 519. m² - 1 = (m - 1)(m + 1). При нечетном m это произведение двух последовательных четных чисел, оно кратно 8 (см. задачу 517). 520. р² - 1 = (р - 1)(р + 1). Далее решение аналогично тому, как в задаче 521. n⁵ - n = (n - 1)n(n + 1)(n² + 1). Произведение (n - 1)n(n + 1) делится на 2, на 3 и, следовательно, на 6; n⁵ - n делится на 5 и при n = 5k, n = 5k + 1, n = 5k + 2, n = 5k + 3, n =5k + 4, что устанавливается подстановкой (см. задачу 510). 522. а⁴ - 1 = (а² + 1)(a - 1)(a + 1); а - 1 делится на 5 при а = 5n + 1, а² + 1 при а = 5n + 2 и при а = 5n + 3, а + 1 - при а = 5n + 4. 523. См. задачи 517 - 519. 524. 7 + 7² + 7³ + 7⁴ +...+ 7n = (7(1 + 7 + 7² + 7³)+7⁵(1 + 7 + 7² + 7³) +...+ 7^{4n - 3}(1 + 7 + 7² + 7³) = 400 (7 + 7⁵ + 7⁹... 7^{4n - 3}). 525. 14; 28. Указание. Пусть искомое число 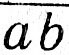= 10а + b. По условию а = ^{10a + b}/₁₄ или 4а = b. Составьте табличку возможных значений а и b. 526. Возможные последние цифры чисел а⁸, b⁸ и с⁸ при а, b, с ∈ N - 1, 5 и 6. Сумма никакой комбинации трех таких цифр не равна 9. 527. (4n + 1)(4m + 1) = 4(4mn + m + n) + 1. 528. n⁴ + 4 = n⁴ + 4n² + 4 - 4n² = (n² + 2)² - (2n)² = (n² + 2 + 2n)(n² + 2 - 2n) = [(n + 1)² + 1]*[(n - 1)² + 1]. 529. (а² + b²)(с² + d²) = а²с² + b²с² + a²d² + b²d² + 2abcd - 2abcd = (ас + bd)² + (bc - ad)². 530. 121 = (10 + 1)², 12 321 = (10² + 10 + 1)², 1 234 321 = = (10³ + 10² + 10 + 1)² и т.д. 531. Для n ≥ 3 имеем: (n - 2)² + (n - 1)² + n² + (n + 1)² + (n + 2)² = 5 (n² + 2), но 5(n² + 2) является квадратом натурального числа лишь в том случае, когда n² + 2 кратно 5. В этом случае n² должно оканчиваться цифрой 3 или 8, что невозможно (окончания квадратов натуральных чисел 0; 1; 4; 5; 6; 9). 532. 2n - 1 = n² - (n - 1)². 533. 4n = (n + 1)² - (n - 1)². 534. 2а² + 2b² = а² + 2аb + b² + а² - 2аb + b² = (а + b)² + (а - b)²535. х⁴ - 2x³ + 6х² + 2х + 1 = х⁴ - 2x³ + х² + х² + 2х + 1 + 4х² = х²(х - 1)² + (х + 1)² + (2х)². 536. За⁴ + 1 = (а⁴ - 2а³ + а²) + (а⁴ - 2а³ + а²) + (а⁴ - 2a² + 1) = (а² + а)² + (а² - а)² + (а² - 1)². 537. а² - b² = (а + b)(а - b), где а и b - данные целые числа. Так как а + b кратно 10, то и а² - b² кратно 10, т. е. а² и b² оканчиваются одной и той же цифрой. 538. Возьмем числа 2, 4, 8, 16, 32, 64, и так без конца. Каждое из них в 2 раза больше предшествующего и между соседними двумя такими числами, как доказал П. Л. Чебышев, содержится хотя бы одно простое число. 539.Указание. Сгруппируйте все равные числа, получите n единиц, n - 1 двоек и т.д. 540. Если х, у и z - длины сторон пифагорова треугольника, то треугольник со сторонами kx, ky и kz, k ∈ N также является пифагоровым, так как (kx)² + (ky)² = (kz)². 541. 1) См. задачу 529. 2) Указание. Разложив числитель и знаменатель на множители, сократите левую дробь; 3) Указание. Знаменатель второй дроби преобразуйте к виду √(1 - х)*(√(1 + x) - √(1 - x)). 542. Пусть x₁, х₂, x₃, ..., x₅₀ ∈ N. Рассмотрим числа x₁, x₁ + x₂, x₁ + x₂ + x₃,..., x₁ + x₂ + x₃ + ...+ x₅₀. Всего их 50. При делении этих чисел на 50 могут получиться лишь остатки, не превосходящие 49. Если ни одно из этих чисел не разделится на 50 без остатка, то по меньшей мере два из них будут давать при делении на 50 один и тот же остаток (так как чисел 50, а остатков не больше 49). Разность между большим из них и меньшим (т. е. сумма нескольких из 50 чисел) разделится на 50 без остатка. 543. Левую часть неравенства обозначим буквой А. А² = ¹/_2²*³²/_4²*⁵²/_6² ... ⁹⁹⁹⁹²/_10000² < ¹/_{2² - 1¹}*³²/_{4² - 1²}*⁵²/_{6² - 1²} ... ⁹⁹⁹⁹²/_{10000² - 1²} = ¹/^1*3*³²/_3*5*⁵²/_5*7 ... ⁹⁹⁹⁹/_10001*9999 = ¹/₁₀₀₀₁ < ¹/₁₀₀₀₀. Следовательно, A < 0,01. 544. 1) Известно, что ^{a + b}/₂ ≥ √ab при а ≥ 0 и b ≥ 0. Имеем: а + b ≥ 2√ab; b + с ≥ 2√bc; a + c ≥ 2 √ac. Перемножая почленно полученные неравенства, находим искомое. 2) ^bc/_a + ^ac/_b + ^ab/_c = ¹/₂(^bc/_a + ^ac/_b) + ¹/₂(^ac/_b + ^ab/_c) + ¹/₂(^ab/_c + ^bc/_a). Далее воспользуйтесь неравенством ^{a + b}/₂ ≥ √ab. 3) x² + y² + z² = ¹/₂(x² + y²) + ¹/₂(y² + z²) + ¹/₂(z² + x²). Затем применить неравенство ^{a + b}/₂ ≥ √ab. 4) x² - 2xy + 2y² - 2x + 3 = x² - 2x(y + 1) + (y + 1)² - (y + 1)² + 2y² + 3 = (x - y - 1)² + y² - 2y + 1 + 1 = (x - y - 1)² + (y - 1)² + 1 > 0. 5) Раскрыв cкобки, сгруппируйте слагаемые в левой части неравенства и воспользуйтесь тем же неравенством. 6) ^{a3 + b3}/₂ - (^{a + b}/₂)³ = ³/₈ (a + b)(a - b)² ≥ 0. 546. Пусть такое число 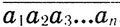. Тогда 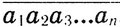= 1979*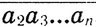, т. е. а₁*10ⁿ + 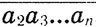= 1979*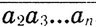, или а₁*10ⁿ = 1978*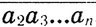. Поэтому 10ⁿ*а₁ = 2*23*43*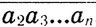. Отсюда следует, что цифра a₁ должна делиться на 23 и на 43, что невозможнo (a₁ ≤ 9). Следовательно, n-значное натуральное число при зачеркивании его первой цифры уменьшиться в 1979 раз не может. 547. 1) 20:(5 - 2)+ 6² ; 2) (20:5*2 + 6)²; 3) 20:5*(2 + 6²); 4) восстановление невозможно. 548. (За - 2b)(За + 2b) = 9а² - 4b². 549. 1) с + 4а²с² - а; 2) 0,8 pq². 551. А = 3,5. 552. β = 6,8. 553. 1)сх; 2) - kp; 3) -n; 4) yz. 554. 10*1 - 9 = 1. 555. В системе счисления с основанием 7. 556. 45 656. 557. 142 857. 558. 301. 559. 27⁶. 560. 41,40. 561. 11, 10. 562. 185² - 15². 563. 48. 564. 405 450. Указание. Если первое трехзначное число а, то второе может быть: 000, 001, 002, ...,999 - а - всего 1000 -а чисел. Но а может быть любым из чисел: 100, 101, 102, ..., 999. Следовательно, на вопрос задачи отвечает сумма: 900 + 899 + 898 + ...+ 2 + 1 =405 450. 565. 6 210 001 000. 566. y = ⁴/₃ x. 567. y =-2x + 5. 568. Линейная функция y = ax + b. 569. y = x² + 2x + 3. 570. y = 2x² - 8x + 12. 571. 2. 572.¹/₃ < k < ³/₂. 573. q < 3. 574. k = -²/₃. 575. 1) k = 1 ²/₃; 2) k < 1 ²/₃. 576. При k > 1 и k ≤ 0. 577. 1) x² + x - 2; 2) не существует. 578. 2(х - 1)(х + 2)(х + 3) + 8 = 2х + 8х² + 2х - 4. 579. x² + 3x + 1. 582. Масса ^{ρ₁m₂ - ρ₂m₁}/_{ρ1 - ρ2}, емкость ^{m₁ - m₂}/_{ρ1 - ρ2}. 583. Первого металла ^{a - c}/_{b - c} m, второго ^{b - a}/_{b - c} m. 584. 729 = 27². 586. 98. 586. 10а + b = а + b² ⇔ 9а = b(b - 1)*b = 9. Число 89. 587. 108. 588. 1979 = 1900 + 10а + b + 1 + 9 + а + b, где а - цифра десятков, b - цифра единиц года рождения Тани. Тогда 11а + 2b = 69 и а - нечетное, 0 ≤ b ≤ 9. Поэтому а = 5, b = 7. Год рождения Тани 1957. 589. См. задачу 588. 590. 1-й способ: 4 отрезка по 7 см и 6 отрезков по 12 см. 591. Павел. Семен поймал 21 рыбу, Павел и Игорь - по 7. 592. 60. 593. Пусть было х пионеров, у стульев и z табуреток. Тогда

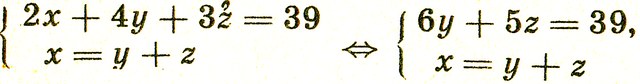
и, очевидно, у = 4, z = 3. 594. 6 трeугольников, 3 квадрата, 1 домик. 595. n = 2, число 178. 597. 36 слагаемых; число 666. 598.

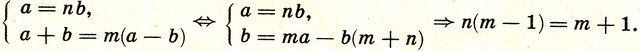
Ясно, что либо m = 2, n = 3, либо m = 3, n = 2, т. е. m + n = 5. 599. 8. 600. 350. 601. Пусть цена аpбуза х, дыни у, граната z. По условию задачи

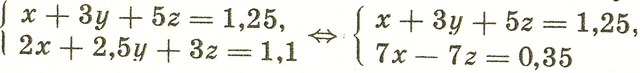
и, следовательно, x > z. Арбуз стоит дороже граната. 602. х² - 22xy = 1978 ⇔ х{х - 2у) = 2*23*43. Тогда либо х = 2k - четное число, либо х - 2у = 2n. При х = 2k, х - 2y = 2{k - y) - четное число, т. е. х{х - 2у) = 4k(k - у), что неверно, так как правая часть не делится на 4. Аналогично при х - 2у = 2m. Уравнение не имеет решений в целых числах. 604. Обозначим числа х и у, тогда х² = у³ = а и а есть степень с показателем 6. Но 100 ≤ а ≤ 10 000. Таких чисел два: a ∈ {3⁶, 4⁶}. Но З⁶ не является кубом двузначного числа (З⁶ = 9³). Поэтому a = 4⁶ и х = 64, у = 16. 605. Уравнение преобразуется к виду х²(а - b) - х(а - b)(а + b) = 0, т. е. при а = b корнем его является любое действительное число, а при а ≠ b корни уравнения х = 0 и х = а + b. Поэтому уравнение имеет единственный корень при а + b = 0, т.е. х = 0. 610. 3 кг. 611. 3 кг. 612. 5. 613. a^{n - 1}. 614. 36. 615. 11, 19 и 14 книг. 616. Если сестре было х лет, когда она была вдвое моложе брата, то сейчас ему 4х, а ей Зх = х + 2х лет. Составив и решив уравнение, получим: брату 40, сестре 30 лет. 617. Обозначив ^a/_b = ^b/_c = ^c/_a имеем: a = bk, b = ck, c = ak, т.е. abc = k³abc. Поэтому k = 1 и a = b = с. 618. Пусть 10a + b - номер дома Коли. Значит, 10а + b - 10b - a = 9(a - b) - номер дома Пети. Но Петя сразу решил задачу, хотя единственное решение имеется лишь при a - b = 8, т. е. при а = 9 и b = 1. Значит, Коля живет в доме № 91. 620. 3155. 621. Степени чисел, оканчивающихся цифрой 3, имеют окончания 3, 9, 7, 1; степени чисел с цифрой единиц 7 имеют окончания 7, 9, 3, 1. 1999 = 1996 + 3 = 4*466 + 3. 1997 = 4*466 + 1. Обе данные степени имеют цифру единиц 7, поэтому их разность кратна 5. 622. 655 = 9*73 + 8. 634. 9:8 = 1,125. 636. Через 9 мин после начала движения первого велосипедиста.

637. Через 8 ²/₁₁ м после начала движения первого велосипедиста. 638. 10 раз. 639. Через 1 ч 40 мин, 2 ¹/₇ ч, 2 ч 30 мин после начала горения. 641. 15. В это число входят и те два парохода, с которыми встречается пароход в Гавре (в момент отхода) и в Нью-Йорке (в момент прихода). Указание. Задача изящно решается графически (рис.73).

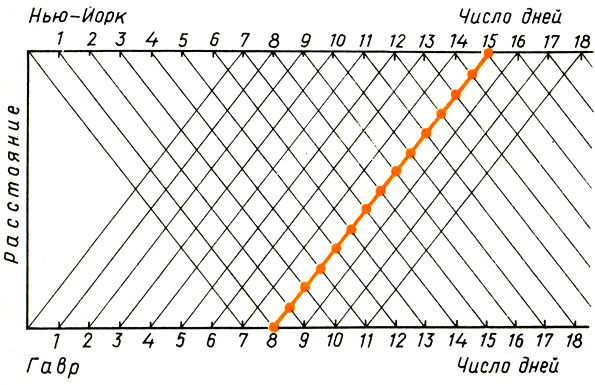
Рис.73

642. 1,11 м; 1,78 м; 2 м; 1,78 м; 1,11 м. 643. Длина стороны вписанного квадрата равна √(x² + (2 - x)²) = √(2x² - 4x + 4), а площадь его S = 2х² - 4х + 4(кв.ед.) = 2[(х² - 2x + 1) + 1]. Наименьшее значение площади вписанного квадрата достигается при х = 1 и равно 2. 644. Контур квадрата со стороной 4 см. 645. Длина участка 50 м, а ширина 25 м.

Глава IV

646. 30°. 647. а) 30°: б) 150°. 648. Задача имеет 3 решения: 1) 80°, 140°, 40°, 100°; 2) 40°, 160°, 20°, 140°; 3) 29°30', 140°, 150°30', 40° - это решение может быть найдено графически (с помощью построений) или с помощью тригонометрии. 649.^{a - c + d - e + b}/₂, ^{a + c + d + e - b}/₂. 651. ≈ 7,5 м. 652. 1,5 м. 653. Первая отливка имеет внутри пустоты, общий объем которых равен 0,03 дм³. 654. 0,02 мм. 655. Длина ребра куба была бы больше 18 м, но меньше 19 м. 656. Останется без изменения. 657. 62,5 г. 658. Площадь трех внутренних кругов больше. 659. Нет. 660. Нет. 662. Возьмем на плоскости две перпендикулярные прямые, параллельные звеньям данной ломаной. Звеньев ломаной, параллельных первой прямой, столько же, сколько звеньев, параллельных второй. Число всех звеньев, параллельных одной из прямых, четно. Поэтому число всех звеньев ломаной кратно 4. 663.Указание. Сумма расстояний от внутренней точки правильного многоугольника до прямых, определяемых сторонами его, равна произведению расстояния от центра многоугольника до стороны его на число сторон. Для доказательства достаточно записать площадь этого многоугольника двумя способами и сравнить записи. 665. Пусть Δ ABC - данный и О - точка пересечения его высот. Постройте точку 0₁, симметричную точке О относительно стороны АВ. Докажите что ∠ 0₁ВС + ∠ 0₁АС = 180,° т. е. что точка 0₁ лежит на окружности, описанной около Δ АВС. Аналогично поступите с точками 0₂ и О₃, симметричными точке О относительно АС и ВС. 669. Можно воспользоваться поворотом данного треугольника вокруг, например, вершины А на 60°. Пусть таким способом получена точка М' из точки М, тогда Δ М'МВ искомый, так как |М'М| = |AM|, |М'В| = |СМ|. 670. Постройте точку М', центрально-симметричную точке М, относительно середины ВС. Δ ВМ'М (а также МСМ') искомый. 671. Пусть 0₁ и 0₂ - середины диагоналей и О - точка пересечения отрезков MN и PQ. Докажите, что PMQN и PO₁QO₂ - параллелограммы с общим центром О; 0₁0₂ - диагональ параллелограмма PO₁Q0₂ - проходит через центр его О. 672. Пусть а, b - длины катетов и с - длина гипотенузы. Имеем: с > а и с > b. Отсюда: са² > аа² и сb² > bb², после сложения: (а² + b²)c > а³ + b³ или c³ > а³ + b³. 673. Пусть А₁, А₂, А₃, ..., A_k - левые концы данных отрезков, а В₁, В₂, В₃, ..., B_k - правые. Любая точка A_i(i = 1, 2, 3, ..., k) лежит левее любой точки B_j (j = 1, 2, 3, ..., k) или совпадает с ней (в противном случае отрезки A_jB_j и А_iВ_i, не имели бы общих точек). Возьмем из точек А самую правую, а из В_j - самую левую. Получим отрезок (или точку в случае совпадения взятых точек), содержащийся в каждом из данных отрезков. 674. Рисунок 74.

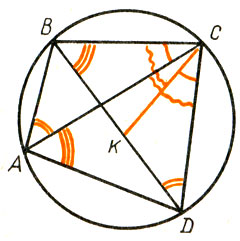
Рис.74

Строим ∠ DCK = ∠ ВСA. ∠ CDK = ∠ CAB - как вписанные, опирающиеся на одну и ту же дугу.

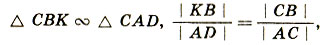
или |DK|*|AC| = |АВ|*|CD| (1). ∠ КСВ = ∠ DCA - по построению, ∠ КВС = ∠ DAC - как вписанные, опирающиеся на одну и ту же дугу. Δ CBK ∼ Δ CAD, ^|KB|/_|AD| = ^|CB|/_|AC|, или |KB|*|AC| = |CB|*|AD| (2). Из (1) и (2) находим: |DK|*|АС| + |KB|*|AС| = |AB|*|CD| + |CB|*|AD|, или |AC|*|BD = |AB|*|CD| + |CB|*|AD|. 675. Рисунок 75.

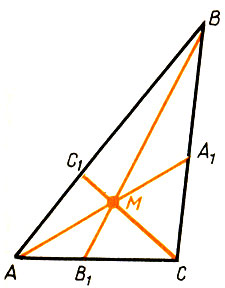
Рис.75

Очевидны пропорции:

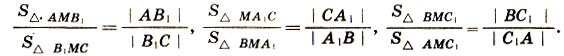
(Каждая пара треугольников имеет одну и ту же высоту.) Перемножая полученные равенства почленно, находим:

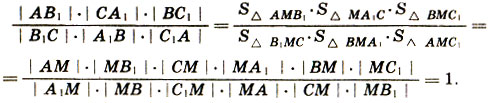
676. Целесообразно вспомогательное построение, показанное на рисунке 76.

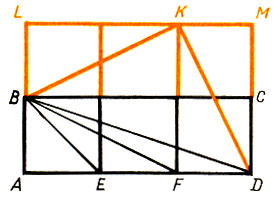
Рис.76

Прямоугольник BLMC равен прямоугольнику ABCD; они составлены из равных квадратов. В Δ BKD |ВК| = |KD|, ∠ BKD = 90°. Значит, ∠ BDK = 45°. Кроме того, ∠ AEB = 45°, ∠ AFB = ∠ MDK. Поэтому ∠ АЕВ + ∠ AFB + ∠ ADB = ∠ BDK + ∠ MDK + ∠ ADB = 90°. 677. Изображенных на рисунке 77 двух и даже трех красок недостаточно.

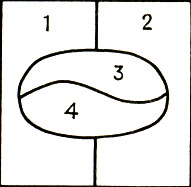
Рис.77

678, 679. В точке пересечения серединного перпендикуляра к АВ и линии реки. 681. Дополнением данного угла до 90°служит угол 36°. Это дополнение следует разделить на 2 равных угла, каждый из которых составляет ¹/₃ данного угла. 682. Постройте угол, равный 19°*19, и вычтите полный угол (19°*19 - 360° = 1°). 683.Указание. a = ¹/₂[(а + b) + (b + с) + (с + а)] - (b + с). 684. Постройте в точке М перпендикуляр к АВ и биссектрисы ∠ ADM и ∠ CDM, где D - точка пересечения построенного перпендикуляра с АС. Точки пересечения этих биссектрис с прямой АВ и будут искомыми. 685. Сначала постройте треугольник по гипотенузе, равной данной диагонали, и катету, равному высоте. По этому треугольнику построить искомый ромб. 686. На сторонах угла от его вершины следует отложить отрезки длиной в половину данного периметра и вписать в угол окружность, касающуюся сторон в полученных точках. Из данной точки провести касательную к этой окружности (разделяющую вершину А и центр окружности). 687. Искомое множество - две окружности, концентрические данным, с радиусами, равными ^{r₁ + r₂}/₂ и ^{r₁ - r₂}/₂. 688. В общем случае получаются четыре окружности. Центры их лежат на прямой, равноудаленной от данных прямых, и находятся от центра данной окружности на расстоянии r + ^d/₂ или ^d/₂ - r, где r - радиус данной окружности, a d - расстояние между данными параллельными прямыми. 689. ≈ 3,4 м и ≈ 0,9 м. 690. Пусть R - радиус данной окружности, х - радиус искомой окружности и О, О₁, 0₂ - соответственно центры данной полуокружности, одной из построенных равных и искомой окружности. Тогда |0₁O₂|² = |0₁0|² + |O₂O|² или (^R/₂ + x)² = (^R/₂)² + (R - x)², откуда х = ^r/₃. 691. Рисунок 78.

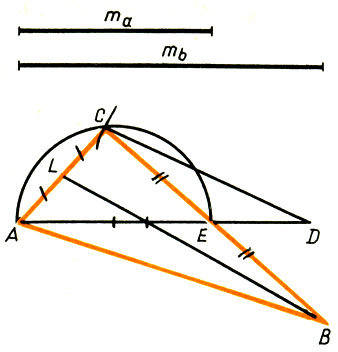
Рис.78

На m_a = |AE|, как на диамерте, постройте полуокружность. Продолжите m_а так, чтобы |ED| = ¹/₃ m_a. Проведите дугу окружности с центром в точке D и радиусом ²/₃ m_b. Точка С пересечения дуги с полуокружностью является

вершиной прямого угла искомого треугольника. По ней может быть построен искомый Δ ABC. 692. Пусть m_а, β_а и h_a(m_a ≥ β_а ≥ h_а) - соответственно медиана, биссектриса и высота, исходящие из вершины А искомого треугольника ABC. Постройте прямоугольный треугольник ADE по гипотенузе |АЕ| = β_а и катету |AD| = h_a с прямым углом при вершине D. Из вершины А, как из центра, радиусом, равным m_а, проведите окружность, пересекающую DE в точке F. Постройте FK ⊥ DE, где К - точка пересечения прямых АЕ и FK. Серединный перпендикуляр к АК пересечется с прямой FK в точке О, которая будет центром описанной около искомого треугольника окружности. В и С - точки пересечения этой окружности с прямой DE. 693. На карте нужно построить множество точек, из которых отрезок АВ виден под углом α, и множество точек, из которых отрезок ВС виден под углом β. Построенные множества пересекаются в двух точках D₁ и D₂. Одна из них и будет искомой. Какая именно - это устанавливается по положению наблюдателя на местности относительно ориентиров А, В, С. 694. Две точки перпендикуляра следует построить по одну сторону от прямой АВ. 695. Можно воспользоваться симметрией относительно прямой АВ. 696. Можно воспользоваться осевой симметрией, пересечением высот треугольника в одной точке, пересечением диагоналей параллелограмма и другими свойствами фигур. 697. Можно воспользоваться осевой симметрией. 698.Указание. Пусть вершина А Δ ABC не уместилась на чертеже. Легко строятся середина отрезка ВС - точка D, средние линии треугольника DE, DF и медианы ВЕ, CF. Третья медиана должна пройти через D и точку пересечения первых двух медиан. 699. С центрами в точках А и В постройте две пересекающиеся дуги одного и того же радиуса. Далее, с центрами в точках пересечения этих дуг, С и D постройте дуги одного и того же радиуса, меньшего |АС|, точки пересечения которых Е и F лежат на прямой АВ между А и В. Такое построение можно повторить. 700. Постройте А₁ и С₁, расстояние между которыми равно |АС|. Из точки А₁ радиусом |АВ| постройте дугу и из точки С₁ радиусом |СВ| - вторую дугу. Точка пересечения этих дуг и будет искомой точкой В₁. 701. Постройте дуги двух окружностей: с центром в точке С радиусом |АВ| и с центром в точке А радиусом |ВС|. Точка пересечения этих дуг - четвертая вершина параллелограмма. 702. 1) Из точки В как центра опишите дугу радиусом |АВ|, а из точки С - радиусом |AC|. Вторая точка пересечения этих дуг D и будет искомой. 2) Построение то же самое. 703. Построение циркулем такое же, как и в задаче 699. 704, 705. Воспользуйтесь построением вершин примыкающих последовательно друг к другу равносторонних треугольников со стороной АВ. 706. Постройте два пересекающихся диаметра. 707. Данную точку А соедините отрезками с концами данного диаметра. Точки D и Е пересечения этих отрезков с окружностью соедините отрезками с концами данного диаметра. Полученные отрезки будут высотами треугольника с вершинами в точке А и концах данного диаметра. Третья высота пройдет через точку А и точку пересечения двух построенных высот и будет искомым перпендикуляром к диаметру. 708. Воспользуйтесь тем, что если медиана к стороне треугольника равна половине этой стороны, то такой треугольник прямоугольный. 709. Воспользуйтесь тем, что с помощью двусторонней линейки легко может быть построен ромб. 710. Сначала постройте угол в 60°. Разделив его пополам, получите угол в 30°. Далее поступите как в задаче 742 построив угол в 60° + 30° = 90°. 711. От произвольной точки А данной окружности постройте 3 равные дуги,

С центром в точках А и D радиусом, равным |АС| = |BD|, постройте две пересекающиеся в точке Е дуги окружностей. Отрезок ОЕ, где О - центр данной окружности, равен стороне вписанного в данную окружность квадрата. Действительно, |DE| = |АЕ| = r√3 (r - радиус данной окружности) и |ЕО| = √(|DE|² - |OD|²) = √(3r² - r²) = r√2. 712. Постройте окружность с центром в точке А и радиусом АО, найдите на ней точку D, симметричную точке О относительно точки А. Дуга окружности с центром в точке D и радиусом, равным радиусу данного круга, пересечет окружность данного круга в искомых точках. 713. Постройте отрезок А₁В и через точку О пересечения его с осью а проведите прямую АО. Найдите точку их пересечения и постройте прямую (А₁0₁). Искомая точка В - пересечение прямых АО и А₁О₁. 714. Рисунок 79.

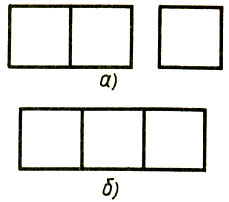
Рис.79

719. Рисунок 80.

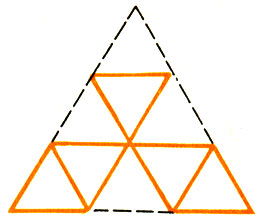
Рис.80

720. 1) Рисунок 81.

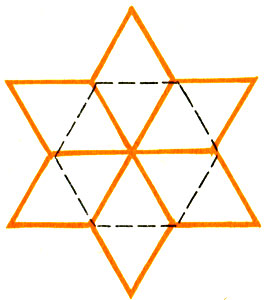
Рис.81

732. Разрезать по диагонали. 734. Рисунок 82.

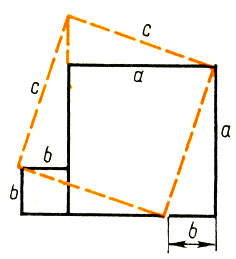
Рис.82

Если а и b - длины сторон данных квадратов, а с - длина стороны третьего квадрата, то с² = а² + b². 735. mn - 1. 736. 6. 738.Указание. Сначала разрежьте на два прямоугольных треугольника. 740. 1) 384; 2) 96; 3) 8; 4) 512. 741. Рисунок 83.

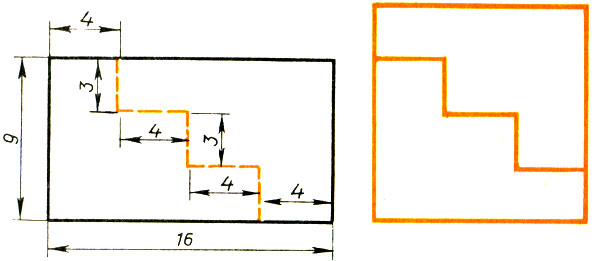
Рис.83

742. Рисунок 84.

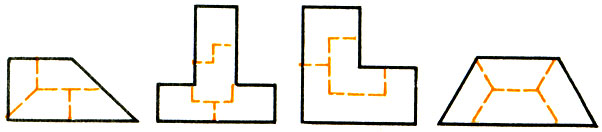
Рис.84

743. 2) данный треугольник сначала разрежьте на два прямоугольных треугольника. 744. Сумма внутренних углов полученных треугольников равна сумме всех внутренних углов стоугольника и всех полных углов с вершинами в отмеченных десяти точках, т.е. 180°*98 + 360°*10. Получается 118 треугольников. 745.746. 10. 747. а) 20; б) 28. 748. 32. 749. 12. 750. 6. 751. 4 раза. 752. Можно воспользоваться "центроискателем" (рис. 85).

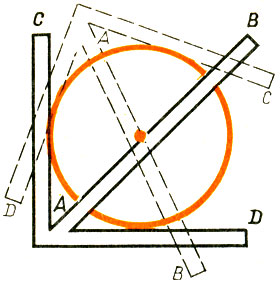
Рис.85

∠ CAD = 90° (АВ - биссектриса этого угла) или чертежным треугольником. Центр круга - точка пересечения двух диаметров. 753. Рисунок 86.

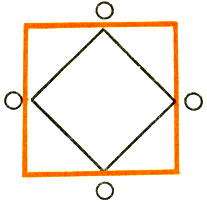
Рис.86

754. Не более 3. Если бы внутренних острых углов было более 3, то многоугольник имел бы более 3 тупых внешних углов и сумма их оказалась бы большэ 360°, что невозможно. 755. Задача о делении угла на 3 равные части с помощью циркуля и линейки разрешима лишь для некоторых определенных углов. 756. Пусть а - длина стороны данного квадрата. Длина стороны искомого квадрата равна длине гипотенузы прямоугольного треугольника с катетами а и 2а. 757.ab. 758. 617 см². 759. 1130 км². 760. √2d, где d - диаметр каждой из заменяемых труб. 761. Пусть r - радиус данного круга. 1) Радиус искомого круга √10r = √(r² + 9r²) - равен длине гипотенузы прямоугольного треугольника с катетами r и 3r. 2) Указание. √13 = √(2² + 3²). 762.^5π/₆. 763. Продолжите стороны ВС и FE до пересечения в точке К, найдите точку пересечения KL и ED и проведите через нее прямую, параллельную АВ. 764.³/₄ кв. единицы. 765. Площадь фигуры, построенной на гипотенузе, равна сумме площадей соответственно построенных на катетах подобных ей фигур. 766. Найдите площадь одного из четырех равных четырехугольников, составляющих данный восьмиугольник. 767. Пусть r - длина радиуса вписанной в треугольник окружности, р + r и q + r - длины катетов. По теореме Пифагора можно найти: r = ¹/₂(-p - q + √(p² + q² + 6pq)). Площадь равна pq. 770. По рисунку 56 видно, что S_I - S_III = S_BD (S_BD - площадь квадрата, построенного на BD) и S_II - S_IV = S_BD. Поэтому S_II - S_I = S_IV - S_III. 771. 1) Нельзя, так как 163*65 не делится на 3; 2) Можно. Для обоснования этого ответа мало установить, что 161*66 делится на 3. Нужно еще найти искомое разбиение. 772. Треугольный, он имеет большую боковую поверхность. 773. Воспользуйтесь центральной симметрией. 774. Каждый из отрезков АВ, АС и ВС примите за основание и достройте трапецию, если это окажется возможным. Число решений зависит от расположения точек А, В и С. 775. 1) Пусть А, В и О - соответственно точки на краях полосы и на ее средней линии. Постройте точки А₁, симметричную точке А относительно точки О и В₁ симметричную точке В относительно точки О. АВ₁ и ВА₁ являются краями полосы. Задача имеет бесконечно много решений, если А, В и О лежат на одной прямой. 776. Постройте точки М₁, симметричную точке М относительно N, и N₁, симметричную точке N относительно М. На АМ₁ и AN₁ лежат две смежные стороны искомого параллелограмма. Дальнейшие построения очевидны. 777. Пусть М, N, Р и Q - данные точки (принадлежат смежным сторонам квадрата). Постройте отрезок NQ, затем MR = NQ и MR ⊥ NQ, пересекающий прямую NQ. Одна из сторон искомого квадрата лежит на PR. Дальнейшее очевидно. 778. Пусть М и N - данные точки смежных сторон квадрата. На MN, как на диаметре, постройте окружность. Найдите середину К той полуокружности, которая опирается на MN и лежит с той же стороны, что и данная точка О. На ОК лежит диагональ искомого квадрата. О дальнейшем вы догадаетесь. 779. Основания биссектрис - вершины вспомогательного равнобедренного треугольника с основанием DE и вершиной F. Через F проведите прямую, параллельную DE. На этой прямой лежат концы основания искомого треугольника. Кроме того, от точек D и Е они отстоят на расстояниях, равных DE. 780. Найдите точку пересечения О с данной прямой серединного перпендикуляра к АВ, концами которого служат данные точки, и опишите окружность из точки О, как центра, радиусом |ОА|. Точки пересечения этой окружности с данной прямой и будут концами основания искомого треугольника. 781. Пусть основание искомого треугольника АС и О - точка пересечения его высот. Постройте АО и СО и перпендикулярные им соответственно лучи с началами в точках С и А - это будут стороны искомого треугольника. 782. Пусть М, N и Р - данные точки. Постройте Δ MNP и его биссектрисы. Точки пересечения продолжений этих биссектрис с окружностью и будут вершинами искомого треугольника. 783. 3) Пусть А, В и С - вершины искомого треугольника (точка А - дана). Должно быть: ∠ ВОС = 180° - ^{∠ ABC}/₂ - ^{∠ АСВ}/₂, ∠ ВАС = 180° - ∠ АВС - ∠ АСВ. 0тсюда: ∠ ВАС = 2∠ ВОС -180°. ∠ ВАС можно построить, тогда определяются вершины В и С искомого треугольника. 784. Задача имеет бесконечно много решений. 785. Рисунок 87. 786. Рисунок 88. 789. Рисунок 89. 791. Рисунок 90. 792. Рисунок 91.

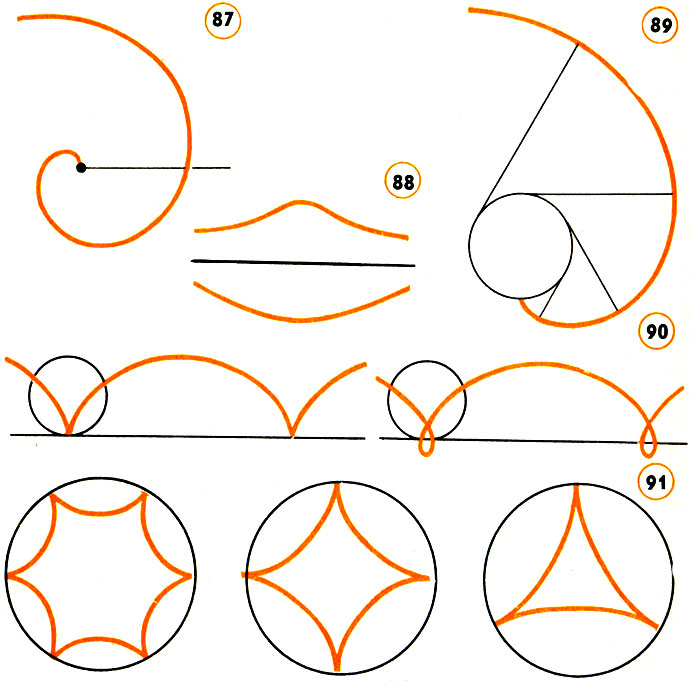
Рис.87., Рис.88., Рис.89., Рис.90., Рис.91

793. 180° ≤ ∠ АВС < 360°. 794. 1) Можно. 2) и 3) Нельзя. 795. 48 см. 796. Прямоугольный. 797. Тупоугольный. 798. 60°, 120°, 60°, 120°. 799. 270°. 800. Нет. 801. Все внутренние углы равны. 802. Можно. Приведите пример. 803. Можно. Приведите пример. 804. Биссектрисы - нет, высоты и медианы - да. 805. Остроугольный или тупоугольный. 806. 9 дм. 807. 2,2 м. 808. Равны. 809. Через центры симметрии параллелограммов. 810. Паркет можно составить из равносторонних треугольников, квадратов и правильных шестиугольников. 811. Не может. 812. Прямая, проходящая через вершину и точку противоположной стороны треугольника, пересекает все его стороны. 813. Нет. 814. 3, так как сумма величин всех внешних углов выпуклого многоугольника равна 360°. 815. Треугольник. 816. Все остальные острые, и сумма их равна 90°. 817. Да. 818. Нельзя. 819. Нельзя. 820. 1) Дельтоид (четырехугольник, составленный из двух равнобедренных (не равных треугольников, приложенных один к другому равными основаниями)); равнобочная трапеция; 2) параллелограмм, отличный от прямоугольника и ромба; 3) прямоугольник или ромб, отличный от квадрата; 4) квадрат. 821. 4. 822. 2n. 823. 1) Не более чем на 5; 2) на 4 части. 824. 1) 7; 2) 9; 3) 19. 825. 7. 826. Квадрат. 827. Первый квадрат - из 4 данных квадратов, второй - из 9. 828.¹/₈. 829. Периметр 8 см, площадь 4 см².

Глава V

832. 8 ч. 833. Задача не имеет решения. 834. 10 раз. 835. На 50. 836. 12,5.837. 11 106. 838. 1050. 839. (70² - 69*70 + 130) = 70(70 - 69) + 130 = 200. 840. 3. 841. 1)65 536; 2) 256; 3) 1. 842. 1) Не существует. 2) Существует число 0. 843. Когда одно число втрое больше другого. 844. Когда один из множителей и делитель равны соответственно 1 или - 1. 845. 1. 846. Например, так 4^{4 + 4/₄}. 847. 9 ч. 848. Например, 5 + 0*n или 4 + (-1)ⁿ. 849. По числу осей симметрии: две, одна и ни одной. 850. 1) Буквы имеют лишь вертикальную ось симметрии; 2) только горизонтальную; 3) только центр симметрии; 4) вертикальную и горизонтальную оси симметрии, а также центр симметрии; 5) буквы не обладают ни осевой, ни центральной симметрией. 851. 0,5 и -1. 852. Леонардом Эйлером (в 1736 г.) и У. Джонсоном (в 1706 г.). 853. Немецким математиком Г. Лейбницем. 854. 14 сентября 1918 г. Советом Народных Комиссаров под председательством В. И. Ленина. 856. А. С. Грибоедов. 858. Начать вопросник можно так: 1) Содержится ли задуманное число среди чисел 1-500? При ответе "Да" спросить: 2) Содержится ли задуманное число среди чисел 1 - 250? При ответе "Нет" задать вопрос: 1) Содержится ли задуманное число среди чисел 501 - 750? Последующие вопросы аналогичны (каждый раз числовой промежуток, содержащий задуманное число, делится пополам). Один из возможных обходов: А - В - С - D - Е - A - Е - B. 861. Приписывание к трехзначному числу такого же числа равносильно умножению этого трехзначного числа на 1001, а 1001 = 7*11*13. 862. Пусть задуманное число 100а + 10b + с и а > с. Обращенное число 100с + 10b + а и разность их 99а - 99с. Эта разность равна 100(а - с - 1) + 90 + (10 - а + с), где а - с -1 - число сотен, 10 - а + с - число единиц. Обращенное для разности число 100(10 - а + с) + 90 + а - с - 1. Сумма будет равна 100(а - с - 1) + 90 + (10 - а + с) + 100(10 - а + с) + 90 + а - с - 1 = 100*9 + 180 + 9 = 1089. 864. 10а + b - задуманное число. Получается: (2а + 5)5 + 10 + b = 10а + b + 35. 865. Каждая цифра задуманного числа в записи шести двузначных чисел встретится 4 раза: 2 раза она будет показывать число десятков и 2 раза - число единиц. При делении суммы шести таких двузначных чисел на 22 получится сумма цифр задуманного числа. 866. Остатки от деления натурального числа и суммы его цифр на 9 равны. У двух чисел, записанных одними и теми же цифрами, остатки от деления на 9 равны и разность этих чисел делится на 9 без остатка. Чтобы найти вычеркнутую цифру, необходимо сумму оставшихся цифр дополнить до ближайшего большего числа, кратного 9. 867. Пусть а - b - первая разность. Тогда вторая будет с - а, третья d - с, четвертая е - d и пятая f - e. Если ограничиться пятью разностями, то сумма их будет равна a - b + c - a + d - с + с - d + f - e = f - b. 869. Пусть m - порядковый номер месяца рождения, t - число этого месяца и п - число лет. Тогда (((100m + t)2 + 8)5 + 4)10 + n + 4 = 10000m +100t + n + 444. 870. В основе этого развлечения лежит представление числа в двоичной системе счисления. Например, 23 = 2⁴ + 2² + 2¹ + 2⁰. Такое представление единственно. Это число записано только на первой, второй, третьей и пятой карточках (см. показатели степеней). Значит, первые числа карточек - это те степени числа 2, которые входят в представление задуманного числа в виде суммы степеней 2 с разными показателями, (1 = 2⁰). 871. Используется равенство: 12 345 679*9 = 111 111 111. 872. Объяснение дает равенство: (4х + 7)25 + у + 125 = 100х + у + 300; х - номер дома, у - возраст. 873. ((а + 3)*5 + 2О)*2 + b + 5 = 1Оа + b + 75, а - число братьев, b - число сестер. 874. Пусть ваш товарищ задумал 6 ч. В этом случае указкой вам придется показать числа на циферблате 14 раз (этого вы не знаете). В восьмой раз вы укажите на 12 ч, а дальше будете указывать каждый раз на 1 ч меньше и сделаете это столько раз (6), сколько единиц недостает вашему товарищу до 20. 877. Весь "секрет" в подборе чисел, характеризующих повороты меньшего круга. Разгадайте его.