Замечательные кривые

785. Спираль Архимеда. Представьте себе, что по радиусу равномерно вращающегося диска с постоянной скоростью ползет муха. Путь, описанный мухой, - это кривая, называемая спиралью Архимеда. Начертите какую-нибудь спираль Архимеда.

786. Синусоида. Сделайте из плотной бумаги, свернув ее несколько раз, трубочку. Разрежьте эту трубочку наклонно. Посмотрите на линию разреза, если развернуть одну из частей этой трубочки. Перерисуйте эту линию на лист бумаги. У вас получится одна из замечательных кривых, называемая синусоидой. Особенно часто с ней приходится встречаться при изучении электротехники и радиотехники.

787. Конхоида Никомеда^*. Постройте кривую линию, называемую конхоидой Никомеда. Сделать это можно так. На листе бумаги проведите прямую АВ и вне ее возьмите точку О (полюс). Затем выберите отрезок а, длина которого пусть будет меньше расстояния от О до АВ . Далее, через точку О проведите прямые и от точки пересечения каждой из этих прямых с АВ откладывайте на ней в обе стороны от АВ отрезок а. Каждый раз вы будете получать две точки искомой кривой. Конхоида Никомеда состоит из двух ветвей, лежащих по разные стороны от АВ.

Попытайтесь догадаться, какой вид будет иметь конхоида Никомеда, если длина отрезка а будет: 1) равна расстоянию от точки О до прямой АВ; 2) больше этого расстояния.

Конхоида Никомеда имеет исторический интерес. За 200 лет до нашей эры она была применена к решению знаменитой задачи о делении произвольного угла на 3 равные части.

Такие же построения, как только что описанные, можно выполнить, взяв вместо прямой АВ окружность. В этом случае полюс О можно брать по-разному. Рассмотрите хотя бы два случая: 1) полюс О совпадает с центром окружности; 2) лежит на окружности и а равняется радиусу этой окружности. Какие линии (их называют улитками Паскаля^**) получатся?

^* (Никомед - греческий математик, живший в III в. до н. э.)

^** (Э. Паскаль (1588-1651) - отец знаменитого французского математика - Б. Паскаля.)

788. Кардиоида. Возьмите два равных кружочка, вырезанных из фанеры (можно взять две одинаковые монеты). Один из этих кружочков закрепите. Второй приложите к первому, отметьте на краю его точку А, наиболее удаленную от центра первого кружка (рис. 57). Затем катите без скольжения подвижный кружочек по неподвижному и наблюдайте, какую линию опишет точка А. Начертите эту линию. Она является одной из улиток Паскаля и называется кардиоидой. В технике эта кривая часто используется для устройства кулачковых механизмов.

Сколько оборотов сделает второй кружок к тому времени, когда он вернется в первоначальное положение? Ответ проверьте, воспользовавшись для этого двумя одинаковыми монетами.

Рис.57

789. Развертка окружности. Возьмите кружочек, выпиленный из фанеры или дощечки, и закрепите его на листе бумаги, лежащем на столе. Намотайте на этот кружочек нить. На конце этой нити сделайте петлю, вставьте в нее карандаш и, натягивая нить, сматывайте ее с кружочка. Тогда конец карандаша на листе бумаги опишет некоторую кривую линию(спираль). Эта линия называется эвольвентой (разверткой) окружности. По какой линии полетел бы с земли камень, если бы на него перестала действовать сила земного притяжения и не мешало бы сопротивление воздуха.

790. Трактриса. Возьмите лист бумаги. Проведите на нем поямую АВ Затем возьмите перочинный ножик, у которого лезвия были бы с двух концов. Раскройте эти лезвия, как показано на рисунке 58, и расположите ножик над листом бумаги как чтобы острия его находились на прямой, перпендикулярной АВ. Кончик полураскрытого лезвия должен находиться на прямой АВ. Свободно держась рукой за это лезвие, перемешайте ножик так, чтобы кончик полураскрытого лезвия перемещался по АВ. Тогда второе, полностью раскрытое лезвие SM острием прочертит наР бумаге тонкую линию. Обведите ее карандашом. Полученная линия называется трактрисой (линией влечения).

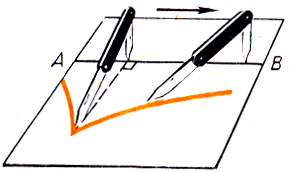
Рис.58

Такую линию можно прочертить и на местности. На песчаной площадке прочертите прямую линию, а затем возьмите шнур и привяжите к нему камень. Встаньте на прочерченную прямую и расположите шнур с камнем так, чтобы он был перпендикулярен этой прямой и камень лежал бы на песке. Затем, держа конец шнура в руке, идите по отмеченной прямой и тяните за собой привязанный к шнуру камень. Линия прочерченная на песке камнем, и будет трактрисой (рис. 59).

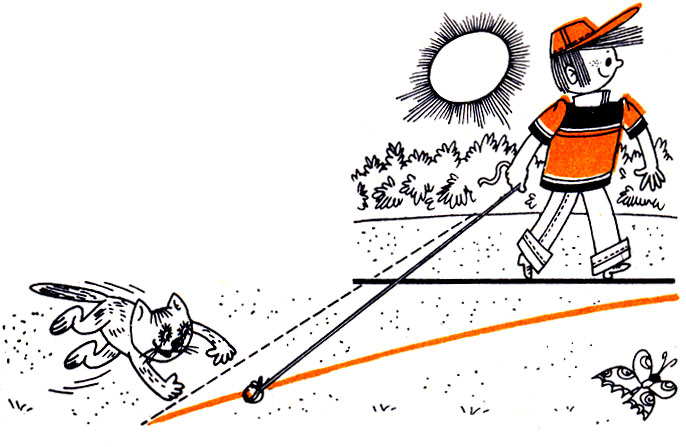
Рис.59

Представьте себе, что трактриса вращается вокруг прямой АВ. Получится поверхность, напоминающая два бесконечных рупора, сложенные своими раструбами (рис.60). Эта поверхность, играющая важную роль в геометрии, называется псевдосферой.

Рис.60

791. Циклоиды. Представьте себе, что по прямой линии без скольжения катится круг. Проследите за тем путем, который опишет при этом точка А, взятая на окружности этого круга (рис. 61). Начертите получившуюся кривую. Она называется циклоидой.

Рис.61

Циклоида обладает многими замечательными свойствами. Вот одно из них.

Давно математики пытались решить такую задачу: какой формы должен быть гладкий желоб, соединяющий две точки А и В (А - выше В), чтобы гладкий металлический шарик скатился по этому желобу из точки А в точку В под действием своего веса в кратчайшее время. Можно подумать, что желоб должен быть прямолинейным. Но это не ак. Может быть, желоб следует выгнуть по дуге окружности, как думал выдающийся итальянский физик, астроном и математик Галилей? Нет, Галилей ошибался. И только в 1696 г. швецарский математик И. Бернулли установил, что желоб должен быть выгнут по циклоиде, опрокинутой вниз.

Пусть к кругу, катящемуся по прямой линии, радиально прикреплена тонкая планочка. Какую линию опишет точка, лежащая на этой планочке и отстоящая от центра круга на расстоянии, большем радиуса? А какая линия получится, если это расстояние будет меньше радиуса? Каждая из этих кривых называется также циклоидой; в первом случае - удлиненной, во втором - укороченной.

792. Гипоциклоиды. Возьмите кусок толстого картона или фанеры и сделайте в нем круговой вырез радиуса 12 см. Из того же материала вырежьте затем три кружка с радиусом 4, 3 и 2 см. Положите кусок картона с вырезанным в нем отверстием на лист бумаги и вложите в этот вырез первый из трех кружков, чтобы он касался края выреза, и отметьте на окружности этого выреза точку (рис. 62). Проследите за тем, какую линию опишет отмеченная точка, когда кружок покатится без скольжения по окружности выреза. Проделайте то же самое со вторым и третьим кружками. Все получившиеся линии называются гипоциклоидами.

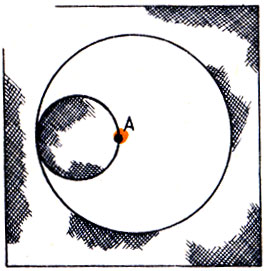
Рис.62