Площади

756. Дан квадрат. Постройте квадрат, площадь которого была бы в 5 раз больше площади данного квадрата.

757. Боковая сторона CD трапеции ABCD имеет длину a, a расстояние от середины АВ до CD равно b. Выразите площадь этой трапеции через а и b.

758. Обхват дерева (длина окружности) - 88 см. Вычислите (с точностью до 1 см²) площадь поперечного сечения этого дерева. Составьте таблицу для нахождения по ней площади поперечного сечения дерева по обхвату его. Сделайте это, например, для таких обхватов: 20, 30, 40, 50, 60 и 70 см, 1 м.

759. Диаметр опаленной площади тайги от взрыва Большого Тунгусского метеорита равен приблизительно 38 км. Какая площадь тайги была опалена?

760. Две водопроводные трубы одного и того же диаметра нужно заменить одной трубой с той же пропускной способностью. Каким должен быть диаметр этой трубы по сравнению с диаметром каждой из заменяемых труб?

761. Дан круг. Постройте круг, площадь которого была бы больше площади данного круга: 1) в 10 раз; 2) в 13 раз.

762. Полуокружность радиуса 1 повернута вокруг конца своего диаметра на 30° (рис. 54). Найдите площадь заштрихованной фигуры.

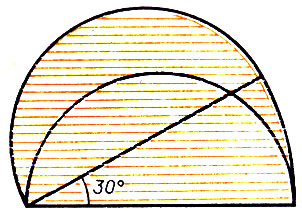
Рис.54

763. Дана фигура ABCDEF, составленная из двух прилежащих прямоугольников (рис. 55). Постройте прямоугольник с основанием АВ, равновеликий данной фигуре.

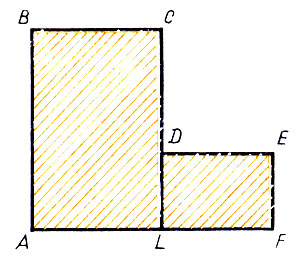
Рис.55

764. Дан треугольник, площадь которого равна 1. Найдите площадь треугольника, образованного медианами данного треугольника.

765. Дан прямоугольный треугольник. 1) Сравните площади полукругов, построенных на гипотенузе и катетах. 2) Сравните площади равносторонних треугольников, построенных на гипотенузе и катетах. 3) На гипотенузе и катетах данного прямоугольного треугольника построены подобные многоугольники, для которых гипотенуза и катеты являются сходственными сторонами. Сравните площади этих многоугольников.

766. Докажите, что площадь правильного восьмиугольника равна произведению длин его наибольшей и наименьшей диагоналей.

767. В прямоугольный треугольник вписана окружность. Точка касания этой окружности делит гипотенузу на отрезки, имеющие длину р и q. Найдите площадь треугольника.

768. Дан выпуклый четырехугольник ABCD. Какое множество точек образуют все такие точки О, для которых площади четырехугольников OBCD и OBAD равны?

769. Найдите на стороне данного треугольника такую точку, чтобы проходящий через нее перпендикуляр к другой стороне делил треугольник на две равновеликие части.

770. (Рис. 56.) ABC - остроугольный треугольник. BD ⊥ AC I, II, III, IV - квадраты. Докажите, что S_II - S_I = S_IY - S_III (S_I, S_II, S_III, S_IV - площади квадратов I, II, III, IV).

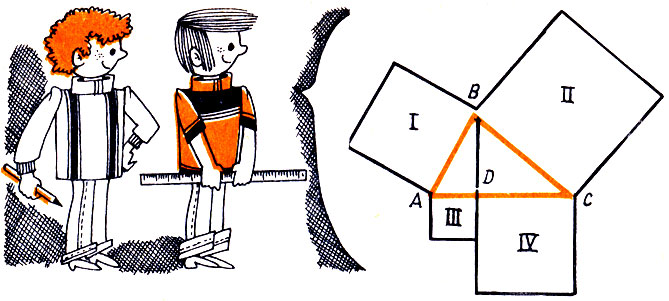
Рис.56

771. Прямоугольник составлен из равных квадратных клеточек: в длину - 163, а в ширину - 65. Можно ли этот прямоугольник разбить на "уголки" по 3 клетки в каждом? 2) Можно ли произвести разбиение на такие "уголки" прямоугольника, имеющего в длину 161, а в ширину 66 клеток?

772. Какой гвоздь крепче держится в деревянной стене (труднее вытащить из стены) - круглый, квадратный или треугольный, если забивать их на одну глубину и площади их поперечных сечений равны?