Ответьте на вопросы

745. Сколько углов, меньших 360°, получится, если из одной точки плоскости провести 3 луча?

746. Сколько получится острых углов, если внутри данного острого угла из его вершины провести 3 луча?

747. Сколько всего треугольников в каждой из двух фигур на рисунке 51?

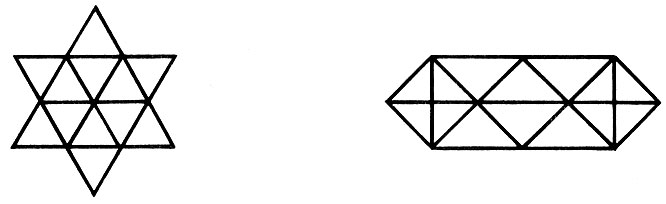
Рис.51

748. Сколько всего квадратов на рисунке 52?

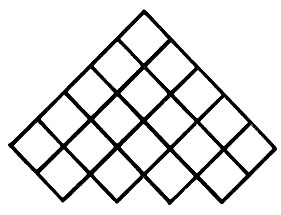
Рис.52

749. Сколько правильных шестиугольников на рисунке 53?

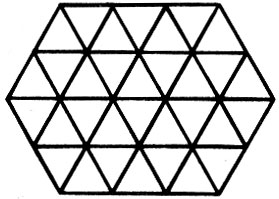
Рис.53

750. Имеется монета. Сколько нужно таких же монет, чтобы их можно было расположить вокруг данной монеты так, чтобы все они касались данной монеты и попарно друг друга?

751. По окружности неподвижного круга перекатывается без скольжения другой круг, радиус которого в 3 раза меньше радиуса неподвижного круга. Сколько раз обернется вокруг своего центра движущийся круг за то время, в течение которого он прокатится вокруг большего круга один раз?

752. Какими простыми приспособлениями можно воспользоваться для нахождения центра круга?

753. По углам бассейна квадратной формы стоят 4 столба. Потребовалось расширить этот бассейн так, чтобы площадь его стала в два раза больше, а форма осталась бы квадратной. Можно ли это сделать, не убирая столбов? Если можно, то как?

754. Исследуйте, какое наибольшее число острых углов может иметь выпуклый многоугольник?

755. Ученик в книге по геометрии прочитал, что задача о делении угла на три равные части с помощью циркуля и линейки неразрешима. "Как же так? - подумал он. - Я очень легко с помощью циркуля и линейки могу разделить на три равные части прямой угол, угол в 45° и некоторые другие". Объясните недоумение ученика.