Докажите

659. Верно ли считать четырехугольник квадратом, если его стороны имеют равные длины?

660. Правильно ли утверждать, что четырехугольник является квадратом, если равны длины его диагоналей? А если равны длины всех четырех отрезков, на которые диагонали делятся точкой их пересечения?

661. Укажите правильные способы проверки того, что четырехугольник является квадратом.

662. На клетчатой бумаге построена замкнутая ломаная линия, каждое звено которой равно стороне клетки и любые два смежных звена взаимно перпендикулярны. Докажите, что число звеньев этой ломаной кратно 4.

663. Дан правильный n-угольник. Докажите, что сумма расстояний от любой внутренней точки его до прямых, определяемых сторонами n-угольника, постоянна (не зависит от выбранной точки). Чему равна эта сумма?

664. Дан равноугольный многоугольник. Докажите, что сумма расстояний от внутренней точки его до прямых, определяемых сторонами многоугольника, постоянна.

665. Докажите, что точки, симметричные точке пересечения высот треугольника относительно трех его сторон, лежат на окружности, описанной около этого треугольника.

666. На сторонах параллелограмма (любого) вне его построены квадраты. Докажите, что отрезки, соединяющие последовательно центры этих квадратов, образуют квадрат.

667. На сторонах треугольника ABC вне его построены равносторонние треугольники АС'В, ВА'С и CB'А. Докажите, что |АА'| = |ВВ'| = |СС'|.

668. На плоскости даны 5000 точек, и никакие три из них не лежат на одной прямой. Докажите, что можно построить 1000 непересекающихся пятиугольников с вершинами в данных точках.

669. Пусть М - произвольная внутренняя точка равностороннего треугольника ABC. Докажите существование треугольника, стороны которого соответственно равны MA, MB и МС.

670. Пусть М - точка пересечения медиан треугольника ABC. Докажите существование треугольника, стороны которого равны AM, BM и СМ.

671. Дан выпуклый четырехугольник ABCD. Середины противоположных сторон его соединены отрезками MN и PQ. Докажите, что средние точки диагоналей данного четырехугольника и точка пересечения отрезков MN и PQ лежат на одной прямой.

672. Докажите, что куб длины гипотенузы прямоугольного треугольника больше суммы кубов длин катетов.

673. На прямой даны k отрезков так, что каждые два из них имеют хотя бы одну общую точку. Докажите, что имеется по крайней мере одна точка, принадлежащая всем этим отрезкам.

674. Теорема Птолемея^*. Для любого вписанного в окружность четырехугольника произведение длин его диагоналей равно сумме произведений длин противоположных сторон. Докажите.

^* (Клавдий Птолемей - древнегреческий ученый, жил во II в. н. э.)

675. Теорема Чевы^*. Если прямые, соединяющие какую-либо внутреннюю точку М треугольника ABC с вершинами, пересекают его стороны АВ, ВС и СА соответственно в точках С₁, А₁ и В₁, то (^|AB₁|/_|B1C|)*(^|CA₁|/_|A1B|)*(^|BC₁|/_|C1A|) = 1. Докажите.

^* (Джованни Чева - итальянский математик, XVII в.)

676. Из трех равных квадратов, как показано на рисунке 40, составлен прямоугольник. Из вершины В его проведены три луча: BE, BF и BD. Докажите (без применения тригонометрии), что ∠ АЕВ + ∠ AFB + ∠ ADB = 90°.

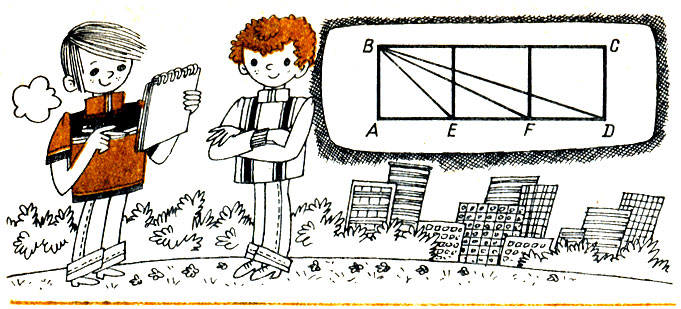
Рис.40

677. Задача четырех красок^*.

^* (Эта задача впервые была поставлена английским математиком Кели в 1879 г.)

Географические карты обычно печатаются в несколько красок. Каждая страна и область страны окрашиваются одним цветом. Для облегчения печатания таких карт обычно удовлетворяются окрашиванием в различные краски лишь примыкающих друг к другу (имеющих общую границу) стран или областей (правильные карты). Докажите, приведя примеры, что двух и трех красок для печатания таких географических (правильных) карт недостаточно.

Многолетняя практика изготовления географических карт приводит к выводу, что четырех красок достаточно. Эта проблема решена и теоретически: четырех красок достаточно для раскраски любой карты на сфере.