Неопределенные уравнения

Решение многих задач приводит к уравнениям не с одной неизвестной или к системам уравнений, в которых уравнений меньше, чем неизвестных. В таких случаях решению обычно помогают некоторые дополнительные условия, сформулированные в задаче. Часто это бывает задание - решить уравнение в целых числах (как, например, в задачах 444-446). Иногда требуется проявить сообразительность и заменить дополнительные условия, явно в задаче не сформулированные. В других случаях необычность уравнения заключается в том, что оно "плохо" решается стандартными методами, т. е. вновь нужно проявить сообразительность. Такие уравнения, системы уравнений и задачи, к ним приводящиеся, решать очень интересно. Попытайтесь решить предложенные далее уравнения и задачи, и вы убедитесь в этом.

Для облегчения вашего труда приведем решение одной такой задачи.

Задача. Какое трехзначное число равно кубу цифры его единиц?

Обозначим искомое число . Тогда по условию задачи 100а + 10b + с = с³ или 10(10а + b) = (с - 1)*с(с + 1). Получили одно уравнение с 3 неизвестными. Левая часть его (а значит, и правая) кратна 10, поэтому хотя бы один из множителей правой части делится или на 10, или на 5. (Явно не сформулированное дополнительное условие.) Но 1 ≤ с ≤ 9, поэтому или с + 1 = 10, или с = 5, или с - 1 = 5. Случай с + 1 = 5 отпадает, так как тогда (5 - 2)(5 - 1)*5 = 60 не является трехзначным числом (10(10а + b) - число трехзначное). Расмотрим каждый из оставшихся трех вариантов.

1) с - 1 = 5 ⇔ с = 6 ⇒ 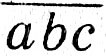= 216;

2) c = 5 ⇒ = 125;

3) с + 1 = 10 ⇔ c = 9 ⇒ = 729.

584. Какое трехзначное число равно кубу цифр его единиц, а также квадрату числа, составленного из его второй и первой цифр?

585. Найдите двузначное число, первая цифра которого равна разности между этим числом и числом, записанным теми же цифрами, но в обратном порядке.

586. Найдите двузначное число, равное сумме числа десятков и квадрата числа единиц.

587. В трехзначном числе зачеркнули среднюю цифру. Полученное двузначное число оказалось в 6 раз меньше исходного трехзначного. Найдите такое трехзначное число.

588. Тане в 1979 г. исполнилось столько лет, какова сумма цифр года ее рождения. В каком году она родилась?

589. Есть ли в вашей школе ученики, которым в этом году исполнится столько лет, какова сумма цифр их года рождения?

590. Сколько существует способов составить отрезок длиной 1 м из отрезков длиной 7 и 12 см?

591. Павел с сыном и Семен с сыном были на рыбалке. Павел поймал столько же рыб, сколько его сын Игорь, а Семен - втрое больше, чем его сын. Всего же они поймали 35 рыб. Как зовут сына Семена? Кто сколько поймал рыб?

592. При делении некоторого числа на 13 и 15 получились одинаковые частные, но при делении на 13 получился остаток 8, а деление на 15 выполнено без остатка. Найдите это число.

593. В комнате, в которой заседал совет дружины, были стулья на 4 ножках и табуретки на 3 ножках. Когда все пионеры уселись, то свободных мест не осталось, а сумма числа ног у сидящих и ножек у сидений оказалась равной 39. Сколько в комнате было стульев и сколько табуреток?

594. Из 36 счетных палочек построили треугольники, квадраты и домики (рис. 31) - всего 10 фигур. Найдите число фигур каждого вида.

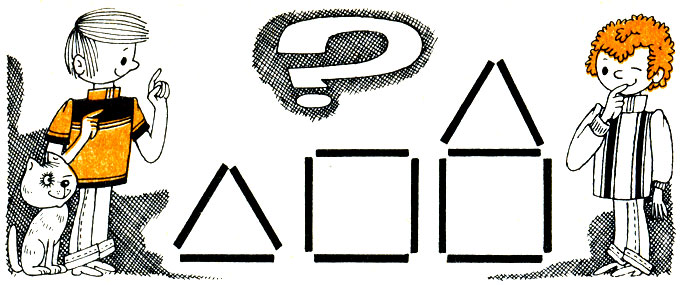
Рис.31

595. Если первую цифру трехзначного числа увеличить на n, а вторую и третью цифру уменьшить на n, то получится число в n раз больше исходного. Найдите n и исходное число.

596. Докажите, что если a, b и c ∈ Q и |а + с| = |b|, то уравнение ах² + bx + с = 0 имеет рациональные корни.

597. Сколько слагаемых суммы 1 + 2 + 3 + 4 + 5 + ... надо взять, чтобы получить трехзначное число, состоящее из одинаковых цифр?

598. Известно, что число а больше числа b в n раз, а сумма чисел а и b больше их разности в m раз. Найдите сумму чисел m и n, если m ∈ N и n ∈ N.

599. В трех ящиках лежат орехи. В первом на 6 орехов меньше, чем в двух других вместе, а во втором - на 10 меньше, чем в первом и третьем. Сколько орехов в третьем ящике?

600. В трехзначном числе зачеркнули цифру сотен, затем полученное двузначное число умножили на 7 и получили вновь исходное трехзначное число. Какое это число?

601. Хозяйка купила арбуз, дыню и гранат. Если бы дыня стоила в 3 раза дороже, а гранат в 5 раз дороже, то хозяйка уплатила бы 1 р. 25 к. А если бы арбуз стоил в два раза, дыня в 2,5 раза, а гранат в 3 раза дороже, то пришлось бы заплатить 1 р. 10 к. Что дороже: арбуз или гранат?

602. Докажите, что уравнение х² - 2ху = 1978 не имеет решений в целых числах.

603. Решите систему уравнений

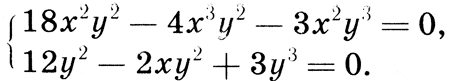
Решение изобразите на координатной плоскости.

604. Найдите два двузначных числа, куб одного из которых равен квадрату другого.

605. При каких значениях a и b уравнение (x - a)³ - (x - b)³ = b³ - a³ имеет единственное решение?

606. Решите в неотрицательных целых числах уравнение x^{n + 3} + y^{n + 3} + z^{n + 3} + xⁿ + yⁿ + zⁿ = x^{n + 2} + y^{n + 2} + z^{n + 2} + x^{n + 1} + y^{n + 1} + z^{n + 1}, где n ≥ 1 и n ∈ N.