Алгебраическая смесь

607. Каким должно быть число, чтобы одна десятая процента от него была равна одной десятой?

608. 1) Когда сумма двух слагаемых меньше каждого из них? 2) Не меньше? 3) Не больше?

609. Какое натуральное число равно произведению всех его натуральных делителей?

610. Кирпич имеет массу 1,5 кг и еще полкирпича. Какова масса кирпича?

611. Какую массу имеет налим, если его масса равна сумме 750 г и массы - того же налима?

612. Какая цифра стоит в конце числа, выражающего произведение 9*11*13*...*19*21?

613. Сколько раз нужно взять слагаемым натуральное число а, чтобы получить аⁿ(n - натуральное число)?

614. Вчера число учеников, присутствующих в классе, было в 8 раз больше числа отсутствующих. Сегодня не пришли еще 2 ученика, и оказалось, что отсутствующих 20% от числа учеников, присутствующих в классе. Сколько всего учеников в классе?

615. На трех полках лежат 44 книги. Если 3 книги с третьей полки переложить на вторую, то на первой и третьей полках книг будет поровну, а на второй вдвое больше, чем на первой. Сколько книг было на каждой полке?

616. Мне сейчас в 4 раза больше лет, чем было моей сестре, когда она была моложе меня вдвое. Сколько лет сейчас каждому из нас, если через 15 лет нам вместе будет 100 лет?

617. Докажите, что если ^a/_b = ^b/_c = ^c/_a, то a = b = c.

618. Школьники Коля и Петя встретились у Пети. Коля сказал: "Разность двузначного номера моего дома и числа, образованного перестановкой его цифр, равна номеру твоего дома. В каком доме я живу?" Петя ответил, что это легкая задача, и сразу ее решил. В каких домах жили школьники?

619. Может ли выражение ^{k + 9}/_{k + 6} быть целым числом? Если да, то при каких целых значениях k?

620. Найдите нечетное четырехзначное число, две средние цифры которого образуют число в пять раз больше числа тысяч и втрое больше числа единиц этого числа.

621. Докажите, что разность 999993¹⁹⁹⁹ - 777777¹⁹⁹⁷ кратна 5.

622. Трехзначное число, две первые цифры которого одинаковы, а цифра единиц 5, разделили на однозначное и в остатке получили 8. Найдите делимое, делитель и частное.

623. Вычислите значение выражения ^{2a - b}/_{3a - b} + ^{5b - a}/_{3a + b}, если известно, что 10а² - Зb² + 5ab = 0 и 9а² - b² ≠ 0.

624. Запишите число 1 000 000 с помощью цифры 5 и знаков действий, употребляя эту цифру возможно меньше раз. А как то же число можно записать с помощью цифры 9 и знаков действий?

625. Запишите с помощью четырех двоек наибольшее число(кроме обычной десятичной записи числа допускается использование степеней).

626. Пусть а - одна из цифр, отличная от 0 и 1. Какое из чисел, записанных в форме а^аа или 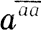, будет больше?

627. Докажите, что если верно равенство ¹/_{a + b + c} = ¹/_a + ¹/_b + ¹/_c,то или а + b = 0, или b + с = 0, или а + c = 0 (аbс ≠ 0, a + b + с ≠ 0).

628. 1) Найдите сумму: 1 + 11 + 111 + 1111 + ... + 1 111 111 111. А если бы в последнем слагаемом было n цифр? 2) Найдите сумму: 9 + 99 + 999 + ...+ 99 999 999 999.

629. Выписаны подряд все натуральные числа от 1 до 60 (включительно). Как в получившемся числе нужно вычеркнуть 100 цифр так, чтобы оставшиеся цифры при сближении их в обычную запись числа выразили наименьшее число? А как нужно вычеркнуть цифры, чтобы получилось наибольшее число?

630. Возьмем все натуральные числа от 1 до 1 000 000 и для каждого из них вычислим сумму его цифр. Для всех получившихся чисел снова найдем суммы их цифр. Так будем продолжать до тех пор, пока все получившиеся числа не будут однозначными. Среди миллиона получившихся чисел встретятся 1 и 2. Каких из этих чисел 1 и 2 будет больше?

631. Возьмем все натуральные числа от 1 до 1000 000. Подсчитайте, сколько среди них таких, которые не делятся ни на одно из чисел от 2 до 5 (включая 2 и 5).

632. Докажите, что число 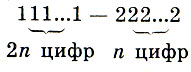является квадратом некоторого натурального числа.

633. Сколько имеется нулей в конце числа, выражающего произведение р¹₁(р²₁р¹₂)(р³₁р²₂p¹₃)...(р¹⁰⁰₁р⁹⁹₂р⁹⁸₃...р¹₁₀₀), где р₁, р₂, р₃,..., р₁₀₀ - последовательные простые числа?

634. Замените в слове "хоккей" буквы цифрами так, чтобы было верным равенство х : о = к,кей.

635. Рассмотрите графики массы бензина (1) и массы серной кислоты (2) в зависимости от объема (рис. 32).

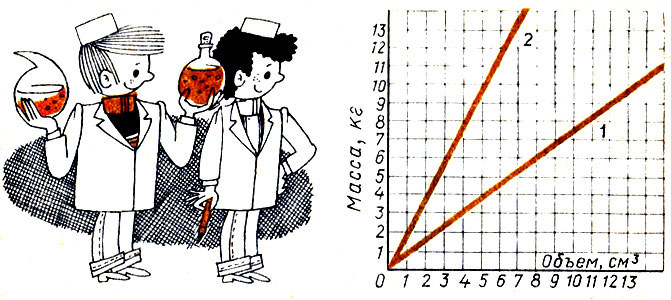
Рис.32

Установите, используя графики: 1) какова масса 12,5 см³ бензина, 5,4 л серной кислоты; 2) какой объем занимает 1 кг, 8 кг бензина; 1 кг, 2,5 кг серной кислоты.

636. Два велосипедиста движутся по круговому пути в одном направлении. Первый проезжает весь круговой путь за 6 мин, а второй - за 4 мин. Второй начинает движение на 3 мин позднее первого и из того же пункта, откуда начал первый. Когда второй велосипедист догонит первого? Решите эту задачу графически.

637. Из пункта С по круговому пути в противоположных направлениях выезжают два велосипедиста. Первый объезжает круг за 12 мин, а второй выезжает из С пятью минутами позже первого и объезжает круг за 10 мин. Когда велосипедисты встретятся? Решите графически.

638. Сколько раз и когда за время от 0 до 12 ч минутная стрелка совпадает с часовой? Решите графически.

639. Две свечи одинаковой длины, но разных диаметров были одновременно зажжены. Известно, что одна из них полностью сгорает за 3 ч, другая - за 5 ч. Горящие свечи три раза фотографировали. Первый раз длины оставшихся частей относились, как 2 : 3, во второй раз как 1 : 2 и в третий раз как 1 : 3. Когда производилось фотографирование? Решите графически.

640. Рассмотрите график движения трех поездов (рис. 33).

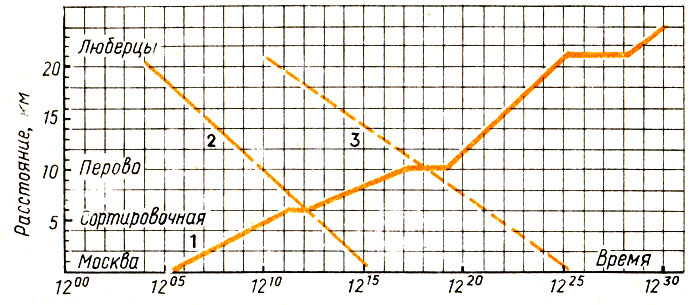
Рис.33

Ответьте по графику на следующие вопросы: 1) Когда прибывает поезд № 1 на станцию Перово и долго ли он стоит на этой станции? 2) Где и когда встречаются поезда № 1 и № 2? 3) На каком участке пути скорость поезда № 1 наибольшая? Вычислите ее. 4) Какой из двух поездов, № 2 или № 3, движется с большей скоростью? 5) Сколько минут идет поезд № 1 от станции Сортировочная до станции Люберцы?

641. На одном научном конгрессе математиков во время завтрака присутствующим была предложена следующая задача. Представьте себе, что каждый день в полдень из Гавра (Франция) в Нью-Йорк (США) отправляется почтовый пароход и в то же время из Нью-Йорка отходит идущий в Гавр пароход той же компании. Каждый из этих пароходов находится в пути ровно 7 суток, и идут они по одному и тому же пути. Сколько пароходов своей компании встретит на своем пути пароход, идущий из Гавра в Нью-Йорк? Решите эту задачу.

642. Арка моста имеет форму дуги параболы (рис. 34).

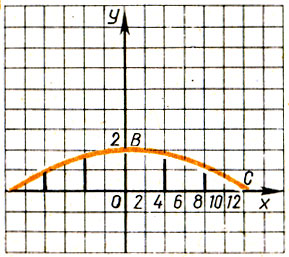
Рис.34

Высота арки 2 м, а длина стягивающей ее хорды 24 м. Арка имеет 5 вертикальных стоек, укрепленных в точках хорды, делящих эту хорду на равные части. Вычислите длины этих стоек.

643. В квадрат со стороной 2 дм вписывается другой квадрат так, что вершины его лежат на сторонах данного квадрата (рис. 35).

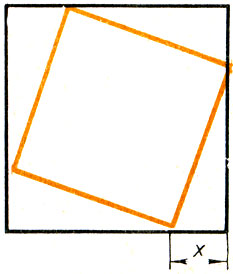
Рис.35

Выразите формулой площадь вписанного квадрата как функцию расстояния между ближайшими вершинами данного и вписанного квадратов, а затем постройте график этой функции. Каким должно быть это расстояние, чтобы вписанный квадрат имел наименьшую площадь? А как эту задачу можно решить, не пользуясь графиком?

644. Из проволоки, длина которой 16 см, нужно согнуть прямоугольный контур, ограничивающий наибольшую площадь. Какими должны быть размеры этого контура?

645. Заготовлен материал для постройки забора длиной 100 м. Требуется огородить этим забором прямоугольный участок для детской площадки. Забор этот должен примыкать к стене дома (рис. 36).

Рис.36

Как поставить этот забор так, чтобы площадь участка была наибольшей?

Математическая шкатулка