Докажите

505. Квадрат нечетного числа - нечетное число.

506. Если квадрат некоторого числа является числом четным, то и само это число - четное.

507. Квадрат четного числа является числом, кратным 4.

508. Разность квадратов двух последовательных натуральных чисел является нечетным числом.

509. Разность квадратов двух последовательных нечетных чисел делится на 8.

510. Сумма кубов любых трех последовательных натуральных чисел кратна 9.

511. Сумма произведения двух последовательных натуральных чисел и большего из них равна квадрату этого большего числа.

512. Произведение двух последовательных четных чисел есть число, кратное 8.

513. Если взять какое-нибудь двузначное число с разными цифрами, переставить в нем цифры и вычесть из взятого числа получившееся, то разность будет делиться на 9. Будет ли это верно для трехзначных чисел (переставляются крайние цифры)?

514. Сумма первых n нечетных чисел равна n².

515. Чтобы двузначное число, оканчивающееся цифрой 5, возвести в квадрат, можно поступить так: число десятков нужно умножить на число, которое на 1 больше числа десятков, и к получившемуся произведению приписать 25. Так, 75² = 5625. Докажите, что это правило верно. Можно ли применить его для трехзначных чисел? Вычислите: 35², 55², 65², 85², 125².

516. Произведение любых трех последовательных натуральных чисел делится на 6.

517. На какие числа делится произведение любых трех последовательных натуральных чисел, сумма которых - нечетное число?

518. Число m³ - m при любом натуральном m делится на 6.

519. Число m² - 1 при m нечетном делится на 8.

520. р² - 1, где р - простое число, большее 3, делится на 24.

521. n⁵ - n делится на 30 при любом натуральном n.

522. Если целое число а не делится на 5, то а⁴ - 1 делится на 5.

523. Разность между кубом любого нечетного числа и самим этим числом делится на 24.

524. 7 + 7² + 7³ + 7⁴ + ... + 7ⁿ делится на 400 при любом натуральном n.

525. Найдите число, обладающее следующим свойством: если зачеркнуть последнюю цифру его, то получится число в 14 раз меньше.

526. Число а⁸ + b⁸ + c⁸ не оканчивается цифрой 9 ни при каких натуральных значениях a, b и с.

527. Произведение нескольких чисел вида 4n + 1 является числом того же вида. Почему достаточно рассмотреть произведение двух чисел этого вида?

528. Всякое число вида n⁴ + 4, где n - натуральное число и n > 1, является составным^*.

^* (Это утверждение часто называют теоремой Софьи Жермен. С. Жермен (1776 -1831) - французская женщина-математик.)

529. Если каждое из двух данных чисел является суммой двух квадратов, то и произведение этих чисел может быть представлено в виде суммы двух квадратов.

530. Числа вида 121, 12321,1234321,...,123...n...321 (n ≤ 9) - полные квадраты.

531. Сумма квадратов 5 последовательных натуральных чисел не может быть квадратом натурального числа.

532. Любое нечетное число можно представить в виде разности квадратов двух чисел.

533. Любое натуральное число, кратное 4, можно представить в виде разности квадратов двух чисел.

534. Двучлен 2а² + 2b² можно представить в виде суммы квадратов двух двучленов.

535. Многочлен х⁴ - 2х³ + 6х² + 2х + 1 можно представить в виде суммы квадратов трех выражений.

536. Двучлен За⁴ + 1 можно представить в виде суммы квадратов трех двучленов.

537. Если сумма двух целых чисел - число, оканчивающееся нулем, то квадраты этих чисел оканчиваются одной и той же цифрой.

538. Великий русский математик Пафнутий Львович Чебышев доказал, что между двумя натуральными числами n и 2n (при n > 1) имеется по крайней мере одно простое число. Воспользовавшись этим результатом, докажите, что простых чисел бесконечно много.

П. Л. ЧЕБЫШЕВ (1821 - 1894) 'Сближение теории с практикой дает самые благотворные результаты, и не одна только практика от этого выигрывает'

539. При любом натуральном n имеет место тождество:

1 + (1 + 2) + (1 + 2 + 3) + ... + (1 + 2 + 3 + ... + n) = 1*n + + 2(n - 1) + 3(n - 2) + ... + n*1.

540. Прямоугольный треугольник, длины сторон которого выражаются натуральными числами, называется пифагоровым. Например, прямоугольный треугольник со сторонами в 3, 4 и 5 единиц длины - пифагоров. Вы, наверное, знаете, что для прямоугольных треугольников сумма квадратов чисел, выражающих длины катетов, равна квадрату числа, выражающего длину гипотенузы (теорема Пифагора). 1) Докажите, что пифагоровых треугольников бесконечно много. 2) Докажите, что если треугольник ABC - пифагоров, то существует бесконечно много подобных ему пифагоровых треугольников. 3) Докажите, что среди всех подобных пифагоровых треугольников существует наименьший (с наименьшими длинами сторон при выбранной единице длины).

541. Докажите тождества:

1) (а² + b²)(с² + d²) = (ас - bd)² + (bc + ad)²;

2)

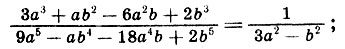
3)

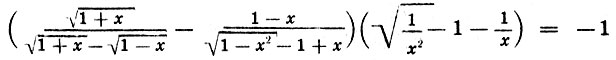
при 0 < х < 1.

542. Докажите, что из 50 любых натуральных чисел всегда можно взять несколько (быть может, и одно из них), сумма которых делится на 50.

543. Докажите, что ¹/₂*³/₄*⁵/₆* ... *⁹⁹⁹⁹/₁₀₀₀₀ < 0,01.

544. Докажите неравенства:

1) (а + b)(b + с)(а + с) ≥ 8abc при а ≥ 0, b ≥ 0 и с ≥ 0;

2) ^bc/_a + ^ac/_b + ^ab/_c ≥ a + b + c при а > 0, b > 0, с > 0;

3) х² + у² + z² ≥ ху + xz + yz при любых действительных х, у и z;

4) х² - 2ху + 2у² - 2х + 3 > 0 при любых действительных x и у;

5) аb(а + b) + bс(b + с) + ас(а + с) ≥ 6abc при а ≥ 0, b ≥ 0, c ≥ 0;

6) ^{a3 + b3}/₂ ≥ (^{a + b}/₂)² при а ≥ 0, b ≥ 0.

545. Докажите, что ¹/_2² + ¹/_3² + ¹/_4² + ... +¹/_100² < 0,99.

546. Может ли n-значное натуральное число при зачеркивании его первой (слева) цифры уменьшиться в 1979 раз?