Где ошибка?

405. Ученик следующим образом выполнил сокращение дроби, получив верный результат (рис. 29). Правильно ли выполнено сокращение?

Рис.29

406. Ученик составил таблицу значений функции у = ¹/_х.

Затем построил точки по найденным их координатам, соединил их отрезками прямых, получив график (рис. 30). Найти ошибки. Что нужно сделать, чтобы устранить ошибки?

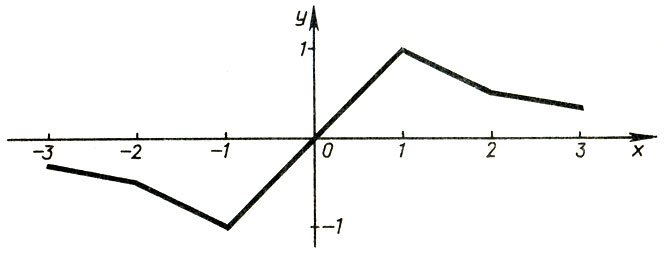
Рис.30

407. Два ученика решили уравнение 5х√2х = 15√8x различными способами. Решение первого ученика:

5х√2х = 15√8x, х√2х = 3*2√2х, √2х(х - 6) = 0,

√2х = 0, или х - 6 = 0, √2х = 0 ⇔ х = 0, х - 6 = 0 ⇔ х= 6.

Ответ: х = 0, х = 6. Решение второго ученика: 5х√2х = 15√8x, x√2x = 3√8x. Возведем обе части уравнения в квадрат: 2х³ = 72х ⇔ 2х(х - 6)(х + 6) = 0. Ответ: х = 0, х = 6, х = -6.

1) Которое решение выполнено правильно? 2) Объясните допущенные ошибки.

408. Два ученика вычисляли при n = 3 значение выражения n + √(1 - 2n + n²) каждый своим способом.

Один из них рассуждал так: n + √(1 - 2n + n²) = n + √(1 - n)² = n + 1 - n = 1 при любых n.

Другой сразу подставлял в алгебраическое выражение заданное значение n : 3 + √(l - 2*3 + З²) = 3 + √4 = 5. 1) Кто из двух верно решил задачу? 2) Найти допущенные ошибки.

409. Решая уравнение ах² + с = 0, ученик нашел его корни

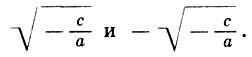
. При подстановке же первого корня в данное уравнение у него получилось следующее:

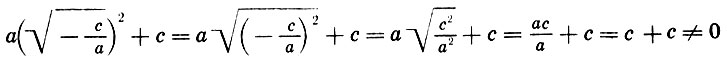
при с ≠ 0. Значит, x = √-^c/_a не является корнем уравнения ах² + с = 0. Совершенно аналогично проверял ученик и второй корень уравнения. Найти ошибки, допущенные учеником.

410. Ученица так выполнила "доказательство" тождества а^-k = ¹/_a^k, k ∈ N : ¹/_a^k = ^a0/_a^k = а^{0 - k} = а^-k. Какую ошибку она допустила?

411. Один ученик рассуждал так: "Известно, что если диагонали параллелограмма взаимно перпендикулярны, то такой параллелограмм - ромб. Нам дан параллелограмм, диагонали которого не являются взаимно перпендикулярными. Следовательно, этот параллелограмм не ромб". В чем ошибка?

412. Витю заинтересовала аксиома параллельных прямых: через точку А, лежащую вне прямой а, в плоскости, определяемой этими точкой и прямой, можно провести не более одной прямой, параллельной а. "Одну прямую можно провести, - подумал он. - Это доказать легко". Через точку А проведем прямую b, перпендикулярную к а, и через А прямую с, перпендикулярную к b, а и с параллельны. Но из моих рассуждений следует, что такая прямая и единственна. В самом деле, перпендикуляр, проведенный через А к а, единствен. Далее, перпендикуляр, проходящий через А к b, тоже единствен. Значит, через А проходит единственная прямая, параллельная а. В чем ошибка?

413. Пассажир, едущий в поезде, захотел узнать скорость поезда. Для этого он подошел к окну вагона, заметил по своим часам время, когда против окна показался телеграфный столб, и, начиная с него, стал считать столбы один за другим. При появлении 24-го столба против окна пассажир опять заметил время. Оказалось, что прошло 2 мин. Зная, что расстояние между столбами 50 м, пассажир сделал вывод: скорость поезда равна 36 ^км/_ч. Какую ошибку допустил пассажир?

414. Известна задача: "Из какой точки земной поверхности нужно выйти, чтобы, пройдя 10 км по меридиану к югу, затем 10 км по параллели к востоку, наконец, снова 10 км по меридиану к северу, вернуться в точку отправления?"

Прежде чем читать дальше, попытайтесь решить эту задачу. Решили? А сейчас познакомьтесь с рассуждениями, которые часто проводятся для решения этой задачи. "Первая и третья части пути проходят по меридианам, но два меридиана имеют только две общие точки: северный полюс и южный. Из южного полюса двигаться на юг нельзя, поэтому он отпадает. Остается единственная возможность - начать движение с северного полюса. Задача имеет единственное решение". Не сможете ли вы обнаружить в этом рассуждении ошибку? Единственное ли решение имеет предложенная задача?