
Математические софизмы
Софизмом называется умышленно ложное умозаключение, которое имеет видимость правильного. Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Особенно часто в математических софизмах выполняются "запрещенные" действия или не учитываются условия применимости теорем, формул и правил. Иногда рассуждения ведутся с использованием ошибочного чертежа или опираются на приводящие к ошибочным заключениям "очевидности". Встречаются софизмы, содержащие и другие ошибки.
В истории развития математики софизмы играли существенную роль. Они способствовали повышению строгости математических рассуждений и содействовали более глубокому уяснению понятий и методов математики. Роль софизмов в развитии математики сходна с той ролью, какую играют непреднамеренные ошибки в математических исследованиях, допускаемые даже выдающимися математиками. И. П. Павлов говорил, что "правильно понятая ошибка - это путь к открытию". Действительно, уяснение ошибок в математических рассуждениях часто содействовало развитию математики.
Пожалуй, особенно поучительна в этом отношении история аксиомы Евклида о параллельных прямых. Сформулировать эту аксиому можно так: через данную точку, лежащую вне данной прямой, можно провести не более одной прямой, параллельной данной (что одну прямую, параллельную данной, можно провести - это доказывается). Это утверждение на протяжении более чем двух тысяч лет пытались доказать, т. е. вывести из остальных аксиом* геометрии, многие выдающиеся математики разных времен и разных народов. Все эти попытки не увенчались успехом. Многочисленные "доказательства", какие были найдены, оказались ошибочными.
* (Аксиомы - это исходные положения, принимаемые без доказательства. Особенности аксиомы параллельных давали повод думать, что она может быть превращена в теорему, т.е. доказана с помощью остальных аксиом геометрии.)
"Строгого доказательства сей истины, - писал великий русский математик Н. И. Лобачевский в 1823 г. в своем учебнике геометрии, - до сих пор не могли сыскать; какие были даны, могут назваться только пояснениями, но не заслуживают быть почтены в полном смысле математическими доказательствами". И все же, несмотря на ошибочность этих "доказательств", они принесли большую пользу развитию геометрии. Были основательно выяснены связи между различными теоремами геометрии. Можно сказать, что эти "доказательства" подготовили одно из величайших достижений в области геометрии и всей математики - создание неевклидовой геометрии. Честь разработки новой геометрии принадлежит нашему великому соотечественнику Н. И. Лобачевскому и венгерскому математику Яношу Бойяи. Н. И. Лобачевский и сам сначала пытался доказать аксиому параллельных, но скоро понял, что этого сделать нельзя. В 1826 г. он пришел к заключению, что утверждение, выражаемое аксиомой о параллельных, при помощи остальных аксиом геометрии доказать нельзя. Путь, идя которым Лобачевский убедился в этом, и привел его к созданию новой геометрии. И этот замечательный вклад в математику был одним из тех, которые прославили русскую науку.
Примеров подобного рода можно было бы привести несколько.
Чем же полезны софизмы для изучающих математику? Что они могут дать?
Разбор софизмов прежде всего развивает логическое мышление, т. е. прививает навыки правильного мышления. Обнаружить ошибку в софизме - это значит осознать ее, а осознание ошибки предупреждает от повторения ее в других математических рассуждениях. Когда ребенок раз притронется к горячему предмету, то впоследствии он постарается этого не делать. Он будет много осторожнее. Так изучающий математику впоследствии проявит больше осторожности.
Далее, что особенно важно, разбор софизмов помогает сознательному усвоению изучаемого математического материала, развивает наблюдательность, вдумчивость и критическое отношение к тому, что изучается. Математические софизмы приучают внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записей и чертежей, за допустимостью обобщений, за законностью выполняемых операций. Все это нужно и важно.
Наконец, разбор софизмов увлекателен. Только очень сухого человека не может увлечь интересный софизм. Как приятно бывает обнаружить ошибку в математическом софизме и тем как бы восстановить истину в ее правах. И чем труднее софизм, тем большее удовлетворение доставляет его анализ.
Имеется немало разных книг, в которых собраны различные софизмы. В конце XIX - начале XX в. особенно большой известностью среди учащихся пользовалась книга Обреимова "Математические софизмы". Этой книжкой зачитывались. Трудно было найти гимназиста, который не читал бы ее. Василию Ивановичу Обреимову, передовому, революционно настроенному деятелю народного образования последних десятилетий XIX и начала XX в. удалось собрать и обработать интересные софизмы. Наверное, этот сборник софизмов имел в виду В. И. Ленин, когда он в одной из своих статей писал, что такие сборники учащимся "приносят свою пользу".
В. И. Ленину в борьбе, которую он вел с врагами рабочего класса, часто приходилось разбирать и разоблачать разнообразные политические софизмы своих противников. Рассуждения по вопросам политики, содержащие замаскированные ошибки, В. И. Ленин сравнивал с математическими софизмами. Он говорил, что эти рассуждения похожи, "...как две капли воды, на те рассуждения, которые математики называют математическими софизмами и в которых, - строго логичным, на первый взгляд, путем, - доказывается, что дважды два пять, что часть больше целого и т. д."*. Эти слова В. И. Ленина показывают, что он знал математические софизмы и это знание помогало ему разоблачать софизмы в политике.
* (Ленин В. И. Поли. собр. соч., т. 8, с. 67.)
В нашей "Математической шкатулке" приводятся ниже некоторые софизмы. При разборе их постарайтесь самостоятельно найти допущенные ошибки и отчетливо понять их. Ну, а если ошибки вы не обнаружите и указания, данные в конце книги, вам не помогут, то обратитесь за разъяснениями к вашему учителю. Помните, что важно добиться отчетливого понимания ошибок, иначе софизмы будут бесполезны.
Наблюдательный и вдумчивый читатель, конечно, заметит, что во многих софизмах допущены одинаковые ошибки. Отчетливое понимание сути таких ошибок значительно облегчит решение последующих аналогичных задач.
369.4 p. = 40 000 к. Возьмем верное равенство: 2 р. = 200 к. и возведем его по частям в квадрат. Мы получим: 4 р. = = 40 000 к. В чем ошибка?
370.5 = 6. Попытаемся доказать, что 5 = 6. С этой целью возьмем числовое тождество: 35 + 10 - 45 = 42 + 12 - 54. Вынесем общие множители левой и правой частей за скобки. Получим: 5(7 + 2 - 9) = 6(7 + 2 - 9). Разделим обе части этого равенства на общий множитель (заключенный в скобки). Получаем 5 = 6. В чем ошибка?
371.2*2 = 5. Найдите ошибку в следующих рассуждениях. Имеем числовое. равенство (верное): 4:4 = 5:5. Вынесем за скобки в каждой части его общий множитель. Получим: 4(1:1) = 5(1:1). Числа в скобках равны, поэтому 4 = 5, или 2*2 = 5.
372.4 = 5. Где допущена ошибка в следующей цепочке равенств: 16 - 36 = 25 - 45, 16 - 36 + 20 1/4 = 25 - 45 + 20 1/4 ,(4 - 9/2)2 = (5 - 9/2)2, 4 - 9/2 = 5 - 9/2, 4 = 5?
373.2*2 = 5. Обозначим: 4 = а, 5 = b, a + b/2 = d .Имеем: а + b = 2d, а = 2d - b, 2d - а = b. Перемножим два последних равенства по частям. Получим: 2da - а2 = 2db - b2. Умножим обе части получившегося равенства на -1 и прибавим к результатам d2. Будем иметь: а2 - 2da + d2 = b2 - 2db + d2 , или (а - d)2 = (b - d)2, откуда a - d = b - d и a = b, т. e. 2*2 = 5. Где допущена ошибка?
374.2 = 3. Имеем: 4 - 10 = 9 - 15, 4 - 10 + 6 1/4 = 9 - 15 + 6 1/4, (2 - 5/2)2 = (3 - 5/2)2, 2 - 5/2 = 3 - 5/2 и окончательно 2 = 3. В чем ошибка?
375.5 = 1. Желая доказать, что 5 = 1, будем рассуждать так. Из чисел 5 и 1 по отдельности вычтем одно и то же число 3. Получим числа 2 и -2. При возведении в квадрат этих чисел получаются равные числа 4 и 4. Значит, должны быть равны и исходные числа 5 и 1. Где ошибка?
376.4 = 8. Возьмем систему уравнений:
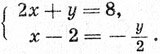
Решим ее способом подстановки. Получим: 4 - у + у = 8, т. е. 4 = 8. В чем здесь дело?
377.Все числа равны между собой. Пусть m ≠ n. Возьмем тождество: m2 - 2mn + n2 = n2 - 2mn + m2. Имеем: (m - n)2 = {n - m)2. Отсюда m - n = n - m, или 2m = 2n, а значит, m = n. В чем ошибка?
378.Расстояние от Земли до Солнца равно толщине волоска. Пусть а(м) - расстояние от Земли до Солнца, а b(м) - толщина волоска. Среднее арифметическое их обозначим через v. Имеем: a + b = 2υ, a = 2υ - b, a - 2υ = - b. Перемножив по частям два последних равенства, получаем: а2 - 2aυ = b2 - 2bυ.Прибавим к каждой части υ2. Получим: а2 - 2aυ + υ2 = b2 - 2bυ + υ2, или ( a - υ)2 = (b - υ)2, т.е. (a - υ) = (b - υ), и, значит, а = b. Где мы ошиблись?
379.Любое, отличное от нуля, число равно противоположному ему числу. Какая ошибка допущена в следующих рассуждениях? Возьмем произвольное, отличное от 0, число а. Обозначим его буквой x, x = a. Обе части этого равенства умножим на -4а. Получим: - 4ах = - 4а2, или - 4ах + 4а2 = 0. К обеим частям этого равенства прибавим х2. Получим: х2 - 4ах + 4а2 = х2, или (х - 2а)2 = х2. Значит, х - 2а = х, но х = а, поэтому а - 2а = а, или -а = а.
380.Любое число равно его половине. Возьмем два равных числа а и b, а = b. Обе части этого равенства умножим на а и затем вычтем из произведений по b2. Получим: а2 - b2 = ab - b2, или (a + b)(a - b) = b(а - b). Отсюда а + b = b, или а + а = а, так как b = а. Значит, 2а = а, или а = a/2. Какая ошибка допущена в этих рассуждениях?
381.Спичка вдвое длиннее телеграфного столба. Пусть a - длина спички (дм) и b - длина столба (дм). Разность между b и а обозначим через с. Имеем: b - а = с, b = a + с. Перемножая два эти равенства по частям, находим: b2 - ab = са + с2. Вычтем из обеих частей bc. Получим: b2 - ab - bc = са + с2 - bc, или b(b - a - с) = -c(b - a - с), откуда b = -c, но с = b - а, поэтому b = a - b, или a = 2b.
382.1 = -1. Начнем с верного числового равенства: 16 - 24 + 9 = 4 - 12 + 9. Перепишем его в виде: (4 - З)2 = (2 - З)2. Значит, 4 - 3 = 2 - 3, т.е. 1 = - 1. Где ошибка?
383.Отрицательное число больше положительного. Возьмем два положительных числа а и b. Сравним два отношения: a/-b и -a/b. Они равны, так как каждое из них равно - a/b. Можем составить пропорцию: a/-b = -a/b. Но если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего. В нашем случае a > - b; следовательно, должно быть -а > b, т.е. отрицательное число больше положительного. В чем ошибка?
384.Из двух неравных чисел первое всегда больше второго. Пусть а и b - произвольные числа и а ≠ b. Имеем: (а - b)2 > 0, т.е. а2 - 2аb + b2 > 0, или a2 + b2 > 2аb. К обеим частям получившегося неравенства прибавим -2b2. Получим: а2 - b2 > 2ab - 2b2, или (а + b)(а - b) > 2b(а - b). После деления обеих частей на а - b имеем: a + b > 2b, откуда следует, что а > b. Где мы ошиблись?
385.Любое число равно числу, в два раза большему его. Пусть а - какое угодно число. Возьмем тождество а2 - а2 = а2 - а2. В левой части его вынесем а за скобки, а правую часть разложим на множители по формуле разности квадратов. Тогда получим: (а - а)а = (а - а)(а + а). Упростив это тождество, получим: а = 2а. В чем здесь ошибка?
386.Любое число равно 0. Найдите ошибку в таком рассуждении. Каково бы ни было число а, верны равенства: (+a)2 = а2 и (-а)2 = а2. Следовательно, (+a)2 = (-а)2, а значит, +a = -а, или 2a = 0, и поэтому a = 0.
387.1 = 2. Где ошибка в следующей цепочке следствий из верного утверждения: 1 - 3 = 4 - 6, 1 - 3 + 9/4 = 4 - 6 + 9/4,
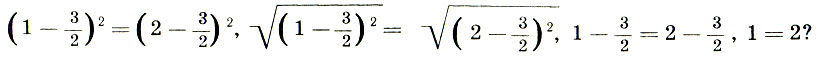
388.Из точки на прямую можно опустить два перпендикуляра. Попытаемся "доказать", что через точку, лежащую вне прямой, к этой прямой можно провести два перпендикуляра. С этой целью возьмем треугольник ABC (рис. 13). На сторонах АВ и ВС этого треугольника, как на диаметрах, построим полуокружности. Пусть эти полуокружности пересекаются со стороной АС в точках Е и D. Соединим точки Е и D прямыми с точкой В. Угол АЕВ прямой, как вписанный, опирающийся на диаметр; угол ВDC также прямой. Следовательно, BE ⊥ AC и BD ⊥ AC. Через точку В проходят два перпендикуляра к прямой АС. В чем ошибка?
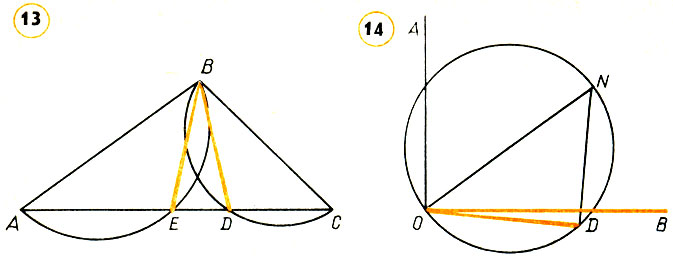
Рис. 13, Рис.14
389.Из точки, взятой на прямой, можно провести к этой прямой два перпендикуляра (лежащие с ней в одной плоскости). Найдите ошибку в таком "доказательстве". Возьмем прямой угол АОВ (рис. 14). Через вершину О проведем внутри угла произвольный луч и на нем от точки О отложим произвольный отрезок ON. Из середины этого отрезка, как центра, опишем окружность, проходящую через точки О и N. Проведем через точку N прямую, параллельную АО. Пусть эта прямая пересекает окружность в точке D. Соединим отрезком точки О и D. Угол ODN, как вписанный, опирающийся на диаметр, прямой, а так как ND || АО, то угол DOA тоже прямой. Следовательно, ОВ ⊥ АО и OD ⊥ АО.
390.Через точку, лежащую вне прямой, можно провести две прямые, параллельные данной прямой. Дана прямая MN и вне ее точка А. Проведем через точку А прямую АВ, параллельную прямой MN. Возьмем на MN некоторую точку С. На отрезке АС, как на диаметре, построим полуокружность. Пусть D - точка пересечения этой полуокружности с перпендикуляром к прямой MN, проходящим через точку С. Через точки А и D проведем прямую. Так как угол CDA прямой, а CD ⊥ MN, то AD - прямая, параллельная MN. Следовательно, через А проходят две прямые, параллельные прямой MN (рис. 15). В чем ошибка?
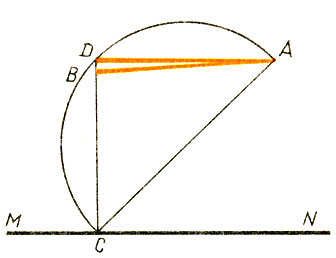
Рис.15
391.Прямой угол равен тупому. Для доказательства выполним следующее построение. Возьмем некоторый отрезок АВ и при концах его А и В построим прямой угол и тупой (рис. 16).
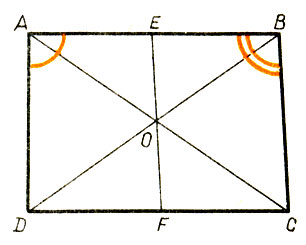
Рис.16
На сторонах этих углов от их вершин отложим равные отрезки AD и ВС. Отрезки АВ и DC разделим каждый пополам и через точки деления проведем к этим отрезкам перпендикуляры. Так как АВ и DC непараллельны, то эти перпендикуляры пересекутся в некоторой точке О. Соединим точку О с точками А, В, С и D отрезками. Получившиеся треугольники AOD и ВОС равны, так как |АО| = |ОВ|, |AD| = |ВС|, |DO| = |СО|, и, значит, ∠ OAD = ∠ ОВС, но ∠ ЕАО = ∠ ЕВО, поэтому ∠ DAE = ∠ СВЕ, т. е. прямой угол равен тупому. Аналогично могут быть рассмотрены случаи, когда точка О лежит на АВ или ниже АВ (рис. 17). Вывод и в этих случаях будет такой же: прямой угол равен тупому. В чем здесь дело?
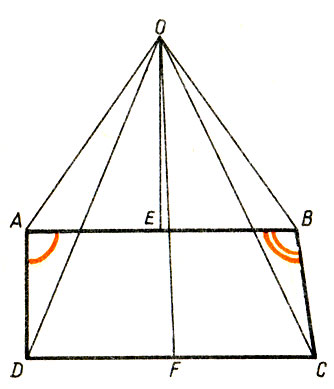
Рис.17
392.Всякий треугольник равнобедренный. Пусть ABC (рис. 18) - произвольный треугольник.
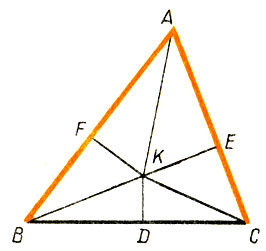
Рис.18
Проведем биссектрису угла А и перпендикуляр к стороне ВС, проходящий через ее середину D. Может оказаться так, что точка пересечения биссектрисы и перпендикуляра (точка К) будет лежать внутри треугольника ABC. Опустим из точки К перпендикуляры КЕ и KF на стороны АС и АВ. Имеем: Δ АЕК = Δ AFK, а значит, |КЕ| = |KF| и |AE| = |AF|. Треугольники BKD и CKD также равны, а поэтому |КВ| = |КС|. Остается рассмотреть прямоугольные треугольники BKF и СКЕ. Они равны, так как |КЕ| = |KF| и |KB| = |КС|. Из равенства этих треугольников вытекает, что |ЕС| = |FB|. Возьмем теперь два равенства: |АЕ| = |AF| и |СЕ| = |BF|. Сложив их по частям, получаем: |АС| = |АВ|. Аналогично можно провести рассуждения в случае, если точка К будет лежать вне треугольника ABC (рис. 19).
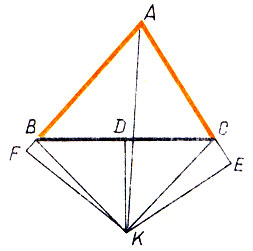
Рис.19
Рассуждения в случае, если точка К будет лежать на стороне ВС (совпадает с D), также не сложны (проведите их сами). Во всех этих случаях приходим к выводу, что треугольник ABC равнобедренный. Значит, любой треугольник равнобедренный. Где ошибка?

393.Всякая окружность имеет два центра. Построим острый угол ABC (рис. 20).
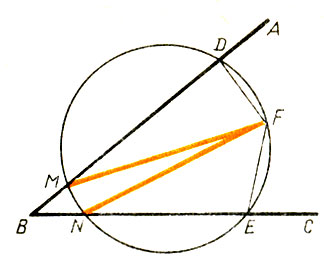
Рис.20
На сторонах его возьмем точки D и Е и через них проведем перпендикуляры к сторонам угла. Пусть эти перпендикуляры пересекаются в точке F. Через три точки D, F и Е проведем окружность. Эта окружность пересечет стороны угла в точках М и N. Отрезки MF и NF должны быть диаметрами построенной окружности, так как на них опираются вписанные в эту окружность прямые углы MDF и NEF. Середины отрезков MF и NF должны быть центрами построенной окружности. Следовательно, окружность имеет два центра. Где ошибка?
394.Внешний угол треугольника равен внутреннему, с ним не смежному. Рассмотрим четырехугольник ABCD, в котором сумма углов А и С равна 180° (рис. 21).
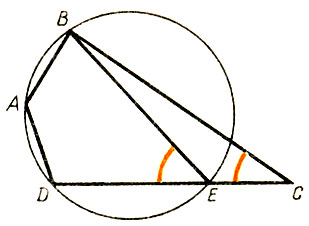
Рис.21
Через вершины D, А и В проведем окружность. Пусть эта окружность пересечет сторону DC в точке Е. Соединим точку Е с точкой В отрезком прямой линии. Тогда ∠ C= 180° - ∠ А (по построению), ∠ BED = 180° - Â (так как четырехугольник ABED вписанный, а значит, сумма противоположных углов его BED и BAD равна 180°). Следовательно, ∠ С= ∠ BED, но ∠ BED - внешний угол треугольника СВЕ, a ∠ C - не смежный с ним внутренний угол этого треугольника. Найдите ошибку.
395.Хорда окружности, не проходящая через центр, равна диаметру. Пусть в окружности проведен диаметр АВ. Через точку В проведем какую-либо хорду ВС, не проходящую через центр; затем через середину этой хорды D и точку А проведем новую хорду АЕ; наконец, точки Е и С соединим отрезком (рис. 22).
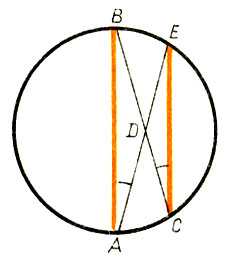
Рис.22
Рассмотрим треугольники ABD и EDC. В них |BD| = |DC| (по построению), ∠ А = ∠ С (как вписанные, опирающиеся на одну и ту же дугу). Кроме того, ∠ BDA = ∠ EDC (как вертикальные). Если же сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны. Значит, Δ BDA = Δ EDC. Поэтому |АВ| = |ЕС|. Где ошибка?
396.Катет равен гипотенузе (рис. 23).
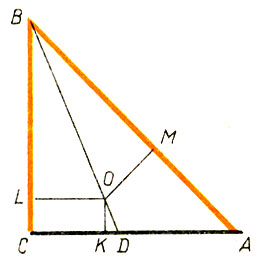
Рис.23
∠ С = 90°, BD - биссектриса угла СВА, |СК| = |КА|, ОК ⊥ С А, О - точка пересечения прямых ОК и BD, ОМ ⊥ АВ, OL ⊥ ВС. Имеем: Δ LBO = Δ МВО, |BL| = |BM|, |ОМ| = |OL| = |СК| = |КА|, Δ КОА = Δ ОМА (ОА - общая сторона, |КА|= |ОМ|, ∠ ОКА = ∠ ОМА = 90°), ∠ ОАК = ∠ MOA, |ОK| = |МА| = |CL|, |ВА| = |ВМ| + |МА|, |ВС| = |ВL| + |LC|, но |ВМ| = |BL|, |МА| = |CL|, и поэтому |ВА| = |ВС|. Где допущена ошибка?
397."Доказательство" теоремы о сумме внутренних углов треугольника, не опирающееся на аксиому параллельных прямых. Возьмем произвольный треугольник ABC (рис. 24),
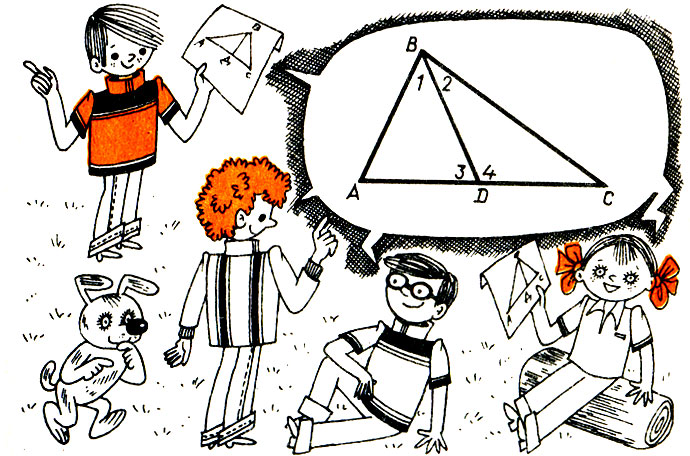
Рис.24
на стороне АС его произвольную точку D и соединим ее отрезком с В. Обозначим искомую сумму внутренних углов треугольника буквой х. Имеем: ∠ A + ∠ 1 + ∠ 3 = x, ∠ С + ∠ 2 + ∠ 4 = х. Сложим по частям эти равенства: (∠ A + ∠ C + ∠ 1 + ∠ 2) + (∠ 3 + ∠ 4) = 2х. Выражение в первых скобках - сумма углов треугольника ABC; она равна х. Выражение во вторых скобках равно 180° (как сумма смежных углов). Имеем: х + 180° = 2х и х = 180°. Верно ли это?
398.64 = 65. Квадрат со стороной, равной 8 единицам длины, разрезан на 4 части, как показано на рисунке 25.
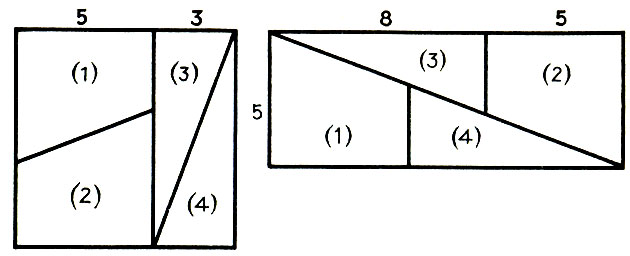
Рис.25
Из этих частей сложен прямоугольник. Основание этого прямоугольника оказалось равным 13 единицам длины, а высота - 5 единицам. Площадь исходного квадрата равна 64 квадратным единицам, а получившегося из него прямоугольника - 65 квадратным единицам. Значит, 64 = 65. В чем ошибка?
399.Длины всех окружностей равны. Соединим неподвижно относительно друг друга два разных круга (с неравными радиусами) так, чтобы центры их совпали. Заставим эти круги перемещаться так, чтобы больший из них покатился без скольжения по прямой линии и сделал полный оборот (рис. 26).
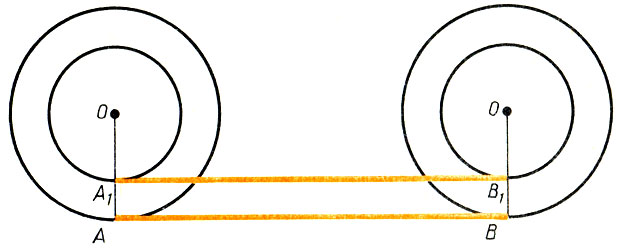
Рис.26
Тогда отрезок АВ прямой линии будет иметь длину, равную длине окружности большего круга (с радиусом ОА). Меньший круг, неподвижно скрепленный с большим, также сделает полный оборот. Отрезок А1В1 будет иметь длину, равную длине окружности меньшего круга (с радиусом ОА1). А так как |АВ| = |А1В1| (как противоположные стороны прямоугольника), то, следовательно, длины этих двух окружностей равны. В чем тут дело?
400.Любые два отрезка параллельных прямых, заключенные между сторонами угла, равны (рис. 27). Так как АВ || CD,то Δ ABE ∼ Δ CDE, и поэтому |AE|/|CE| = |BE|/|DE|, или |АЕ |×|DE| = |СЕ||BE|. Получившееся равенство умножим по частям на |AB| - |CD|. Получим: |АЕ||DE|(|АВ| - |CD|)= |CE||BE|×|AB| - |CD|), или |АЕ||DE||АВ| - |AЕ||DE||CD| = |CE||BE||AB| - |CE||BE||CD|, что можно переписать так: |АЕ||DE||АВ| - |СЕ||ВЕ||АВ| = |АЕ||DE||CD| - |CE||BE||CD|, или |АВ|(|АЕ||DE| - |CE||BE|)= |CD|(|АЕ||DE| - |CE||BE|), откуда получаем: |АВ| = |CD|. Где ошибка?
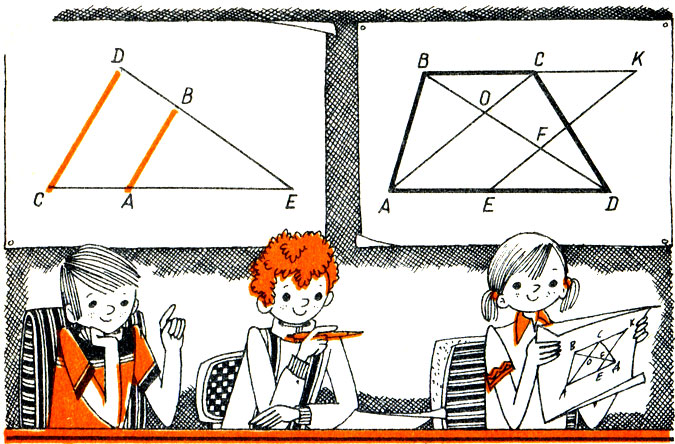
Рис.27., Рис.28
401.Длина средней линии трапеции равна нулю (рис. 28). ABCD - трапеция, ВС || AD, О - точка пересечения диагоналей. Выполним следующее построение: ВК - продолжение ВС, |ВК| = |AD|, |DE| = |BC|. Введем обозначения: |ВО| = х, |OF| = у, |FD| = z. Имеем: Δ DEF ∼ Δ ВКЕ, откуда |BF|/||FD = |BK|/|DE|, или x + y/z = |AD|/|BC| (1). Δ BOC ∼ Δ AOD, откуда |DO|/|BO| = |AD|/|BC|, или y + z/x = |AD|/|BC| (2). Сравнив (1) и (2), получаем: x + y/z = y + z/x, или x + y/z = -y - z/-x. Обозначив каждое из этих отношении через t, получаем: x + y/z = t,-y - z/-x = t, откуда имеем: х + у = tz, - y - z= -tx. Просуммировав полученные равенства по частям, получаем: х + у - у - z = t(z - х), или x + y - y - z/z - x = t, и поэтому x - z/z - x = x + y/z, или x + y/z = -1. Но x + y/z = |AD|/|BC| и поэтому |AD|/|BC| = -1, т.е. |AD| = -|ВС|. Значит, |AD| + |ВС| = 0 и |AD| + |BC|/2 = 0. Где ошибка?
402."Новое доказательство" теоремы Пифагора. Возьмем прямоугольный треугольник с катетами а и B, гипотенузой с и острым углом α, противолежащим катету а. Имеем: а = csin α, b = сcosα, откуда а2 = с2sin2α, b2 = с2cos2α. Просуммировав по частям эти равенства, получаем: а2 + b2 = c2(sin2α + cos2α). Но sin2α + cos2α = 1, и поэтому а2 + b2 = с2. Подвергните критике это "доказательство".
403.Квадрат любого числа равен 1. Пусть m - какое угодно число. Обозначим: x = y = m4/4. Имеем: √x = √y и x - √x = y - √y или х - у = √х - √y что можно переписать так: (√x + √y)(√x - √y) = √x - √y. Из полученного равенства находим: √x + √y = 1. Следовательно, 2 √х = 1, но х = m4/4, и поэтому 2 √m4/4 = 1, или m2 = 1. Где ошибка?
404.2 = 4. Имеем тождество: cos2х = 1 - sin2x, откуда (cos2х)3/2 = (1 - sin2х)3/2, или cos3х = (1 - sin2x)3/2. К обеим частям полученного равенства прибавим 3. В полученное равенство подставим вместо х 180°. Будем иметь: -1 + 3 = 1 + 3, т. е. 2 = 4.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'