"Не", "И", "Или"

Чтобы научиться правильно рассуждать, надо изучить правильные способы, методы рассуждений. Анализом методов рассуждений занимается наука логика, а исследованием и изучением математических рассуждений - математическая логика. В математической логике для исследований применяется математический аппарат.

Чтобы правильно рассуждать, надо научиться из простых высказываний правильно составлять сложные высказывания, или, как говорится в математической логике, выполнять операции над высказываниями. При этом необходимо знать, вытекает ли истинность сложных высказываний из истинности составляющих их более простых предложений.

Простейшие операции над высказываниями.

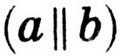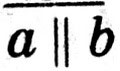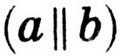Отрицание. Обозначается, как и в обыденной речи, частицей "не" или словом "неверно". Отрицанием высказывания, например: "Прямая а параллельна прямой b" является предложение "Прямая а не параллельна прямой b или "Неверно, что прямая а параллельна прямой b". В символической форме это отрицание записывается так: или ¬ . Ясно, что отрицание ¬ А истинно тогда и только тогда, когда ложно А, и наоборот.

Конъюнкция. Два высказывания могут быть соединены союзом "и". Из высказываний "Число 5 простое" (обозначим его А), "Число 5 нечетное" (обозначим его В) можно составить сложное высказывание А и В (обозначается 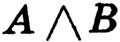): "Число 5 простое и нечетное". Такое сложное высказывание 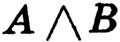называется конъюнкцией высказываний А и В. Если каждое из высказываний А и В истинно, то истинно и высказывание 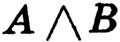. Если хотя бы одно из высказываний А, В является ложным, то ложным будет и высказывание .

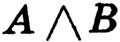Дизъюнкция. Два высказывания могут образовать сложное высказывание, будучи соединены союзом "или", употребляемым в неразделительном смысле. А или В означает истинность хотя бы одного из высказываний А и В. Такое сложное высказывание называется дизъюнкцией высказываний А и В. Обозначается . Например, дизъюнкция 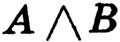высказываний А ("Число 5 простое") и В ("Число 5 четное") - высказывание "Число 5 простое или четное". В этом случае А истинное, В ложное, 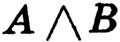- истинное высказывание. Дизъюнкция истинных высказываний А и ¬B 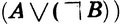. "Число 5 простое или нечетное" есть истинное высказывание. Примером дизъюнкции может служить и высказывание "а ≤ b, верное тогда, когда верно хотя бы одно из высказываний а < b или a = b".

Приведем несколько упражнений, которые помогут лучше понять роль и значение операций отрицания, конъюнкции и дизъюнкции в структуре сложных высказываний.

302. Какие из приведенных ниже высказываний верные, а какие неверные:

1) Деление а : b без остатка возможно, если число а кратно числу b, b ≠ 0.

2) Число 4 удовлетворяет неравенству х < 8 и неравенству х > 2,5.

3) Не все простые числа нечетные.

4) Число 0,5 удовлетворяет неравенствам: а) х < 0,5; б) х ≤ 0,5; в) х ≥ 0,5; г) х > 0,5.

5) Каждый треугольник имеет два тупых угла.

303. Сформулируйте отрицания высказываний:

1) Все числа, делящиеся на 3, нечетные.

2) Вертикальные углы равны.

3) Равные углы вертикальны.

4) Каждому натуральному числу предшествует одно натуральное число.

304. Истинны или ложны высказывания:

1)

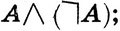
2)

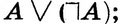
З)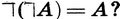

Предложенные в задаче 304 сложные высказывания имеют в логике специальные названия: ¬(¬ А) = А - закон двойного отрицания;

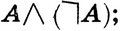  - закон противоречия;

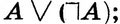  - закон исключенного третьего. Эти высказывания часто применяются в доказательствах теорем, а законы противоречия и исключенного третьего лежат в основе доказательства методом сведения к противоречию (методом "от противного", как говорят иногда в школе).