Учитесь правильно рассуждать

"Однажды, в самом начале учебного года, мне пришлось услышать разговор двух девочек. Старшая из них перешла в шестой класс, младшая - в пятый. Девочки делились своими впечатлениями об уроках, учителях, подругах, о новых предметах. Шестиклассницу очень удивили уроки геометрии: "Вот чудеса,- говорила она. - пришла учительница в класс, нарисовала на доске два равных треугольника, а потом целый урок доказывала нам, что они равны. Никак не пойму: зачем это нужно?". "А как же ты будешь отвечать?" - спросила младшая девочка. "Выучу по учебнику... вот только очень трудно запомнить, где какую букву нужно поставить..." Таким рассказом начинается интересная книжка А. И. Фетисова "О доказательстве в геометрии" (1954).

Н. К. Крупская (1869-1939). 'Когда ребята поймут связь математики с другими отраслями знаний, математика оживет, будет увлекать, из трудного предмета превратится в отрасль знания'

Мне тоже много раз приходилось слышать от шестиклассников, что они не понимают, зачем нужно рассуждениями доказывать геометрические теоремы. "Что вертикальные углы равны, - говорили они, - это и так видно". "Что в равнобедренном треугольнике углы при основании равны - это показывает чертеж. Чего же тут еще рассуждать?" - удивлялись они. Нельзя было оставлять такие вопросы без ответа, вот и приходилось беседовать с учащимися о математических доказательствах. Об одной из таких бесед я и расскажу.

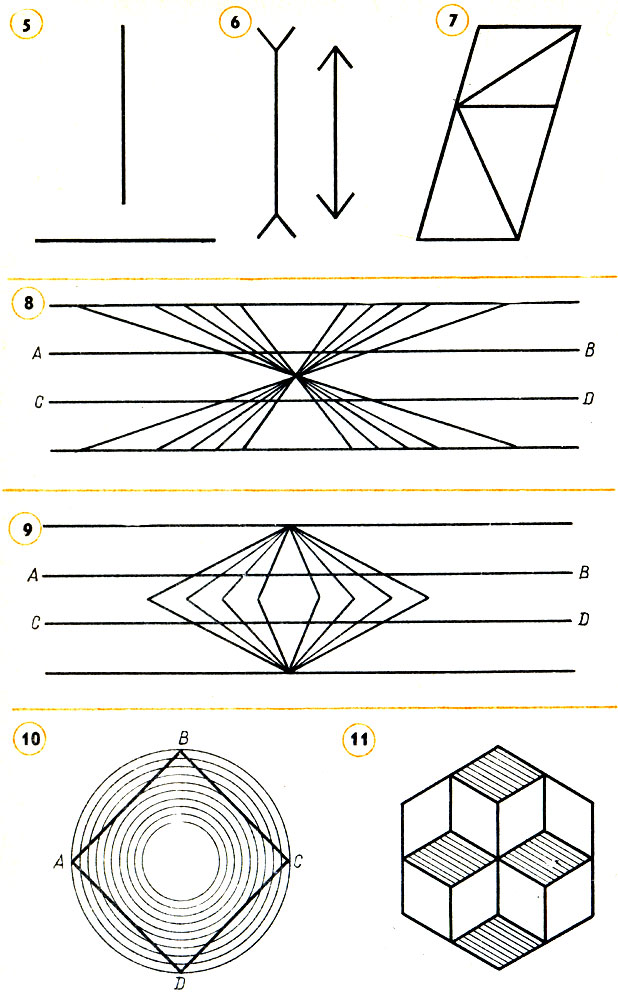
Рис. 5., Рис. 6., Рис. 7., Рис. 8., Рис. 9., Рис. 10., Рис. 11

Шестиклассник Боря сказал мне, что геометрические теоремы надо доказывать чертежами. "Посмотришь на чертеж, и сразу видно, что теорема верна. Глаз не обманет", - говорил он. У меня под руками на этот раз оказалось несколько интересных рисунков, и я показал их Боре. "Сравни длины вот этих двух отрезков", - попросил я (рис. 5). Боря посмотрел на чертеж и, усмехнувшись, сказал: "Конечно, вертикальный длиннее". "А сейчас?" - и я показал второй чертеж (рис. 6). "Левый длиннее", - заявил Боря. "А вот два параллелограмма (рис. 7), и в каждом из них проведена диагональ. Сравни их". И на этот раз Боря уверенно заявил, что нижняя диагональ длиннее. Тогда я предложил Боре линейкой измерить все сравниваемые отрезки. Он охотно взялся за это, ничуть не сомневаясь, что измерения только подтвердят его ответы. Но измерения показали, что на каждом из этих чертежей длины сравниваемых отрезков равны. Боря не поверил этому и снова начал измерять. Новые измерения привели его к тому же выводу. Лицо Бори выражало растерянность. Он моргал глазами, силясь понять, в чем же дело.

Дальше я показал Боре еще три чертежа (рис. 8, 9, 10) и попросил установить - прямые или кривые линии АВ и CD на этих чертежах? Ответ был таким: "Конечно, кривые". И снова Боря растерялся, когда приложил к этим линиям линейку и обнаружил, что все линии прямые.

Наконец я показал Боре еще один рисунок (рис. 11) и спросил, что изображено на нем. Он внимательно посмотрел и сказал: "Тут изображены три кубика: один вверху, а два внизу". "Посмотри снова, - попросил я, - так как мне кажется, что вверху два кубика, а под ними один". Боря снова посмотрел. "А ведь верно, два вверху и один внизу. Почему же мне вначале показалось, что наоборот? Постойте, постоите, опять два внизу, а один вверху". Боря удивленно потер глаза. "Как же так? Снова два сверху, а один снизу. Чудно".

После всех этих демонстраций мне осталось спросить Борю: "Можно ли доказывать чертежами теоремы? Не могут ли наши глаза обманывать нас?" И Боря честно признал, что рассмотрение чертежей может привести к ошибочным заключениям, потом немного подумал и, оживившись, сказал: "Глазам доверять нельзя, а надо измерять". Пришлось мне продолжить беседу. Я сказал Боре, что всякие измерения неточны, да к тому же выполнить их часто бывает трудно. Может, например, не оказаться под руками нужных инструментов. Но главное - в другом. Измерить можно один или несколько отрезков, один или несколько углов и т. д. Но все фигуры рассматриваемого вида измерить невозможно. И то, что верно для каких-нибудь двух измеренных треугольников, может оказаться неверным для двух других треугольников. Как же быть? Вывод сделал сам Боря. "Делать нечего, придется учиться рассуждать, чтобы доказывать теоремы". Это был хороший вывод. Действительно, надо учиться правильно, логически рассуждать.

В заключение беседы я рассказал Боре то, что недавно слышал и наблюдал на одном уроке геометрии в 6-м классе. На этом уроке перед изучением теоремы о свойствах равнобедренного треугольника была проведена опытная работа. Каждый ученик в своей тетради начертил равнобедренный треугольник и с помощью транспортира измерил углы при основании этого треугольника. После этого был сделан вывод, что, наверно, углы при основании равнобедренного треугольника равны. Сформулирована была теорема, затем учитель сказал: "Мы проверили теорему об углах при основании равнобедренного треугольника для 35 таких треугольников (на уроке было 35 учеников), и для них эта теорема оказалась верной. Правильно ли отсюда сделать вывод, что она будет верна для любого равнобедренного треугольника? А может быть, для тридцать шестого треугольника, который мы начертим, она будет неверной? Как же быть? На помощь приходят рассуждения, и за несколько минут мы сделаем то, что невозможно сделать с помощью опытной проверки, если бы даже этой проверкой занимались все ученики всех школ. При помощи логических рассуждений мы докажем эту теорему для всевозможных равнобедренных треугольников. Вот какую важную роль играют в геометрии рассуждения". Дальше на уроке было проведено доказательство этой теоремы.

Я объяснил Боре, что доказательство любой теоремы - это цепочка логических умозаключений, сводящих доказываемую теорему к ранее доказанным теоремам и введенным аксиомам и определениям. Но ранее доказанные теоремы сводятся к теоремам, которые были доказаны еще раньше. В конечном счете, все теоремы опираются на принятые аксиомы.

В доказательствах теорем постоянно используются математические понятия. Большинство математических понятий определяются. При определении нового понятия употребляются другие понятия, которые должны быть уже известными. Но такое сведение одних понятий к другим не может быть бесконечным. Должны быть исходные понятия, первичные, несводимые к другим, неопределяемые. Таковы, например, понятия: множества, точки, числа, расстояния и другие. Их можно пояснить, описать, привести конкретные примеры, но не определить. Все это учащимся нужно хорошо усвоить, и тогда многие трудности изучения математики будут преодолены.

Боря слушал меня очень внимательно. И когда мы расстались, он сказал, что понял, зачем надо доказывать теоремы так, как это делается на уроках.

Есть такая наука, она называется логикой, которая учит, как нужно рассуждать, чтобы наше мышление было определенным, связным, последовательным, доказательным и непротиворечивым. Как человек, не знающий правил арифметики и грамматики, не может правильно считать и грамотно писать, так и человек, не знающий правил логики, не может без ошибок рассуждать и действовать. Значит, советский человек, чтобы принести больше пользы своей великой Родине, делу построения коммунизма, должен владеть логикой.

Человеку, занимающемуся математикой, очень часто приходится определять понятия, выяснять связи между ними, рассматривать, на какие группы (виды) могут быть подразделены фигуры, числа, уравнения функции и т. д. Но особенно часто в математике приходится путем рассуждений выводить разнообразные формулы, правила и доказывать теоремы. Не случайно находились такие математики, которые думали, что математика - это наука "о производстве необходимых умозаключений". Такой взгляд на математику односторонен, но верно то, что без логики не может быть математики. А это значит, что для успешного изучения математики, надо настойчиво учиться правильно рассуждать. Это значит также, что само изучение математики очень полезно для овладения правилами и законами мышления. Не без оснований называют иногда математику "оселком для ума". Не случайно М. И. Калинин говорил ученикам средних школ Ленинского района г. Москвы, что "...математика дисциплинирует ум, приучает к логическому мышлению. Недаром говорят, что математика - это гимнастика ума. Я не сомневаюсь, что голова у вас ломится от мыслей, но эти мысли надо упорядочить, дисциплинировать, направить, если можно так выразиться, в русло полезной работы. Вот математика и поможет вам справиться с этой задачей".

Жизнь, особенно техника, а также очень многие науки, ставят перед математикой все новые и новые задачи. Математикам приходится разрабатывать вопросы математической теории и создавать методы, обеспечивающие решения возникающих в различных науках и практике задач. Как же поступают математики? Решение всякой задачи по математике - это прежде всего цепь рассуждений. Вычисления, преобразования, построения, которыми так часто приходится пользоваться для решения задач, невозможны без логических рассуждений: они направляются рассуждениями. Значит, в математике невозможно обойтись без логики.

Приведем несколько примеров. В 1781 г. была открыта планета Уран. Наблюдения за движением этой планеты в конце XVIII - начале XIX в. показали, что оно несколько отличается от математически предсказанного движения. Объяснить это отличие можно лишь влиянием на Уран новой, неизвестной планетыг находящейся еще дальше от Солнца. И вот французский ученый Леверье (1811-1877), исходя из отклонений в движении Урана, логически рассуждая и выполнив довольно сложные вычисления, указал положение этой планеты на небе. И действительно, в указанном Леверье участке неба 23 сентября 1846 г. астроном Галле нашел новую планету, названную потом Нептуном. Это открытие является одним из выдающихся достижений человеческого мышления. Так же была открыта и девятая, следующая планета, названная Плутоном.

М. И. Калинин (1875-1946) 'Все школьники должны помнить, что только тот человек будет иметь какое-нибудь значение в общественной и государственной жизни, на любом полезном поприще, кто умеет работать систематично, со знанием дела'

Математика помогла также открытию многих малых планет, например Цереры. Цереру впервые наблюдал астроном Пиацци, но из-за перерыва в наблюдениях потерял ее. На помощь пришел знаменитый математик К. Ф. Гаусс. Располагая некоторыми данными о новой планете, полученными Пиацци, он вычислил ее орбиту. И действительно, по указаниям, данным Гауссом, Церера была вновь найдена.

Вот еще один пример, иллюстрирующий значение логики в математике. В глубокой древности люди пытались опытным путем найти отношение длины окружности к ее диаметру, т.е. пытались найти число, показывающее, во сколько длина окружности больше длины ее диаметра. Этим числом, обозначаемым буквой π (пи)^*, приходится пользоваться при вычислении по известной длине диаметра длины окружности и площади круга, а также для решения многих других важных задач.

^* (Это обозначение впервые применил в 1706 г. английский математик У. Джонс, а общепринятым оно стало с 1736 г., когда его стал систематически Употреблять Л. Эйлер.)

Значит, надо было с необходимой точностью вычислить значение π. Опытное вычисление могло дать лишь грубо приближенный результат. На ранних ступенях человеческой культуры пользовались этими неточными значениями л. В Древнем Египте, например, свыше 3000 лет назад считали число π равным 3. В III в. до н. э. один из величайших математиков Древней Греции, талантливый изобретатель, верный сын своей родины, погибший от врагов ее, Архимед без измерений, одними лишь рассуждениями и вычислениями, нашел для числа л довольно точное значение: 3 ¹/₇(архимедово число). Позднее другие математики, воспользовавшись открытием Архимеда, вычислили π с еще большей точностью. Так, в XVI в. немецкий математик Лудольф, затратив очень много времени, вычислил 35 десятичных знаков этого числа. Лудольфово значение π равно: 3,14159265358979323846264338327950288. Вычисления более точных значений л после Лудольфа, основанные уже на иных соображениях, не прекращались. В 1873 г. математик Шенкс вычислил 527 десятичных знаков этого числа. Шенкс, правда, вычислил всего 707 десятичных знаков, но, начиная с 528-го, его знаки оказались ошибочными. Такое Приближенное значение π, какое было найдено Шенксом, наверное, не имеет практической ценности. И все же вычисление новых знаков числа л продолжалось. В 1946-1947 гг. в Англии и США с помощью ЭВМ вычислили 808 десятичных знаков этого числа, в 1949 г. - 2035 знаков, а затем 3089 знаков. В настоящее время известно свыше 10 000 знаков числа л, и вычисление все новых знаков приносит некоторую практическую пользу: так проверяют вычислительные возможности современных ЭВМ, программного обеспечения к ним. Мы видим, что логические рассуждения, позволившие развить геометрию и другие части математики, дают возможность вычислить число л и многие другие часто используемые числа (константы) с любой степенью точности, без каких-либо измерений.

Все сказанное заставляет сделать вывод о необходимости настойчивого овладения умением логически рассуждать. Каждому школьнику надо упорно учиться правильно мыслить.

Может быть, это следует делать лишь в старших классах средней школы? Учиться логически рассуждать нужно много и постоянно во всех классах школы.