В мире чисел (системы счисления)

Любое натуральное число в десятичной системе счисления представляется в виде суммы N = а_n10ⁿ + а_{n - 1}10^{n - 1} + a_n-210^n-2 + ... + a₁10 + a₀, где a₀, a₁,..., a_{n - 1}, a_n - числа 0,1,2, ...,8,9, означающие, что число N состоит из а₀ единиц, а₁ десятков, а₂ сотен и т. д. Запись 27 354 выражает, например, что в составе числа имеются 4 единицы, 5 десятков, 3 сотни, 7 тысяч и 2 десятка тысяч (27 354 = 2*10⁴ + 7*10³ + 3*10² + 5*10 + 4). В общем случае для обозначения таких сумм часто пользуются записью: a_na_{n - 1}...a₁a₀, где a_n,a_{n - 1},a_{n - 2}, ...,a₁,a₀ - цифры в записи числа.

Почему за основание десятичной системы счисления принимается число 10? Никаких особых математических преимуществ у числа 10 по сравнению с другими нет. Использование его, как основания системы счисления исторически объясняется только тем, что первым счетным аппаратом человека были десять пальцев рук. Счет по пальцам рук, которым пользовались наши предки, положил начало системе счисления.

В прошлом люди пользовались и другими системами счисления. Применялись, например, двенадцатеричная, шестиде-сятеричная, пятеричная, двадцатеричная системы с основаниями 12, 60, 5, 20. Следы этих систем сохранились в языках, мерах, денежных единицах разных стран и народов.

В связи с развитием ЭВМ широкое применение нашли двоичная, восьмеричная, троичная, двоично-восьмеричная системы. Для современных вычислительных машин эти системы оказались более удобными, чем десятичная.

Как же переводить числа из одной системы счисления в другую? Пусть, например, нужно число 1421 из десятичной системы счисления перевести в восьмеричную^*.

^* (Для различения чисел между собой в зависимости от применяемой системы счисления с основанием р приняты записи вида: 1421₁₀ - в десятичной системе, 10 100₂ - в двоичной системе и т. п.)

Можно поступить так. Разделим данное число на 8; получим в частном 177 и в остатке 5. Частное 177 снова разделим на 8, получим новое частное 22 и остаток 1. Это частное еще раз делим на 8, получаем частное 2 и остаток 6. Деление продолжаем до тех пор, пока в частном не получим число меньше 8. Записать этот процесс деления можно так:

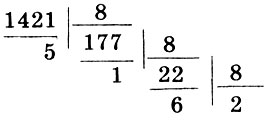
Имеем последовательно: 22 = 2*8 + 6, 177 =(2*8 + 6)*8 + 1 и 1421 = ((2*8+ 6)*8 + 1)*8 + 5, т. е. 1421 = 2*8³ + 6*8² + 1*8 + 5. Следовательно, 1421₁₀ = 2615₈. Как видим, чтобы записать данное число 1421₁₀ в системе счисления с основанием 8, достаточно выписать друг за другом последнее частное 2 и остатки 6, 1, 5.

Пусть, наоборот, нужно число из недесятичной системы перевести в десятичную. Как это сделать, покажем на примере. Возьмем число 23401₅. Его можно записать в виде суммы и произвести затем необходимые вычисления. 23401₅ = 2*5⁴ + 3*5³ + 4*5²+ 0*5 + 1 = 1726₁₀.

Особенно проста система счисления с основанием 2. В ней используются только 0 и 1. На первом справа месте записывается число единиц - 0 или 1; на втором - число двоек - 0 или 1; на третьем - число четверок - 0 или 1; на четвертом - число восьмерок и т. д. Вот несколько записей чисел в этой системе счисления: 101110₂ = 46₁₀, 101010011₂ = 393₁₀.

Мы уже знаем, как от десятичной записи числа перейти к записи при другом основании и обратно. Особо рассмотрим еще переход от записи числа при основании 2 к записи при основании 8. Он очень прост и используется при записи чисел, с которыми оперирует ЭВМ. В основе этого перехода лежит представление чисел от 0 до 7 в двоичной системе счисления. Составим табличку:

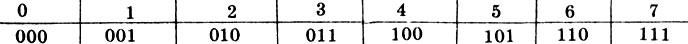
В верхней строке этой таблички записаны цифры, используемые в системе счисления с основанием 8, а под ними - записи соответствующих чисел в двоичной системе счисления, так называемые триады.

П. С. Лаплас (1749-1827) 'Мысль выражать числа десятью знаками... настолько простая, что... трудно понять, насколько она удивительна'

Как пользоваться этой табличкой, покажем на нескольких примерах.

1. Пусть имеем число 101010011₂. Разобьем его справа налево на грани по 3 цифры в каждой. Начальная (старшая) грань может содержать три, две или одну цифру. Имеем: 101010011. Но каждая из этих граней в системе с основанием 8 дает одну из цифр 0, 1, 2, ..., 6, 7. Поэтому в нашем случае получаем число 523₈.
2. Если имеется число, записанное в восьмеричной системе, то для перевода его в двойную достаточно вместо каждой цифры данного числа записать соответствующую ей триаду. Так число 73333653₈ равно 111011011011110101011₂.
3. Мы видим, что переход от десятичной системы к двоичной лучше осуществлять с помощью восьмеричной системы. Пусть, например, нужно число 172₁₀ представить в двоичной системе. Получаем:
   
   
   Следовательно, 172₁₀ = 254₈ = 010101100₂ = 10101100₂. Переводить десятичное число в восьмеричное легче, а переход от восьмеричной системы к двоичной очень прост.

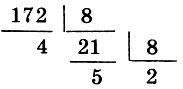
Как выполнять действия в системе счисления, отличной от десятичной? Можно, конечно, переводить данные числа в десятичную систему и выполнять указанные над ними действия. Но можно и не переходить к привычной для нас десятичной системе, а выполнять действия в заданной системе по аналогии с выполнением их в десятичной. "Жить" в не десятичной системе счисления для нас непривычно, но вполне возможно. Нужно только все время помнить, каково основание системы.

Вот несколько примеров непосредственного выполнения действий в недесятичных системах счисления. Как они производятся, вы легко разберетесь сами.

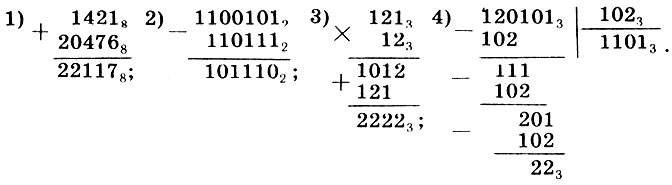
Особенно просты действия с двоичными числами, стоит только запомнить простые таблицы сложения и умножения.

Вот они:

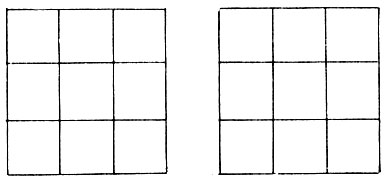
Как пользоваться этими таблицами, показывают примеры:

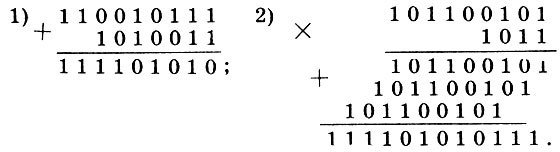
Более подробно о системах счисления можно прочитать в брошюре С. В. Фомина^*.

^* (См.:Фомин С. В. Системы счисления. М., 1975.)

239. В какой системе счисления 2*2 = 10?

240. Один шестиклассник о себе написал так: "Пальцев у меня 24, на каждой руке 5, а на ногах 12". Как же так могло быть?

241. Запишите: 1) число 2456₁₀ по пятеричной системе счисления; 2) 321₁₀ по троичной; 3) 64₁₀ по двоичной.

242. Запишите в десятичной системе счисления следующие числа: 1) 100101₂; 2) 120012₃; 3) 403200₅; 4) 5042₈.

243. Во сколько раз увеличится число 325₆, если: 1) приписать справа один нуль; 2) приписать справа три нуля?

244. Во сколько раз уменьшится число 212000₃, если: 1) отбросить справа один нуль; 2) отбросить три нуля?

245. В какой системе счисления: 1) 23₁₀ запишется как 212; 2) 33₁₀ как 53; 3) 42₁₀ как 52?

246. Какое из чисел больше: 1) 3₁₀ или 3₈; 2) 14₁₀ или 14₈; 3) 111₂ или 111₈; 4) 0,11₂ или 0,11₁₀; 5) 0,21₁₀ или 0,21₈; 6) 0,2₁₀ или 0,1463₈; 7) 0,2₈ или 0,1463₈; 8) ¹/₅₁₀ или ¹/₅₈ ; 9) ¹/₈₁₀ или ¹/₁₀₈?

247. Выполните указанные действия: 1) 1011001₂ + 1000111₂; 2) 11011₂*1101₂; 3) 322₅*14₅; 4) 1111010101111₂ : 1011₂; 5) 3240₅ + 4023₅; 6) 1421₈ + 20476₈; 7) 23265₈ - 4762₈; 8) 121₃*12₃; 9) 120101₃ : 102₃.

248. В какой системе счисления будет: 1) 4*4 = 31; 2) 3*3 = 10?

249. Установите, в какой системе счисления выполнялось каждое из следующих действий: 1) 23 + 14 = 42; 2) 71 - 36 = 33; 3) 14*2 = 30; 4) 55:4 = 13.

250. Если 4*4 = 20, то чему равно произведение 5*5 (в той же системе счисления)?

251. Число, записанное в десятичной системе счисления, оканчивается цифрой 5. Будет ли это число кратно 5, если его записать в системе счисления с основанием 3?

252. Хорошо известны признаки делимости натуральных чисел на 2, 3, 4, 5, 9, 10 в десятичной системе счисления. Будут ли верны эти признаки в иных системах счисления, например при основании 3, 5?

253. Выполните действия: 1) 1000000₂:1000₂; 2) 11₂:100₂; 3) 11₂:101₂; 4) 12₃:100₃; 5) 10₃:11₃.

254. Запишите дроби ⁷/₁₆, ¹/₃ , ⁴/₅ по аналогии с десятичными дробями в виде двоичных дробей.

255. Дроби ⁴/₂₇ и ⁴/₅ запишите в виде троичных дробей.

256. 1) Запишите текущий год в двоичной системе счисления; 2) запишите в троичной системе счисления год своего рождения.

257. Составьте таблицы сложения и умножения однозначных чисел в системе счисления с основаниями: 1) 3; 2) 6.

258. Расшифруйте высказывание: "Мне 1111 лет, и я учусь в III классе".

259. Имеется набор из 60 цифр 0 и 1, разбитых на 30 групп так, что в каждую группу входят 0 и 1. Из каждой такой группы берется по одной цифре и составляется число. Очевидно, что мы так можем составить в двоичной системе любое число, имеющее не более 30 двоичных знаков, а всего таких чисел будет 230. Если бы имелся набор из 60 цифр 0, 1, 2, разбитых на 20 групп так, что в каждую группу входят 0, 1 и 2, то в троичной системе счисления можно было бы составить З20 чисел. Аналогично, имея набор из 60 цифр 0, 1, 2, 3, разбитых на 15 одинаковых групп, можно составить в четверичной системе 416 чисел, в десятичной - соответственно 106. Какая из этих систем наиболее экономична (в какой из них можно записать больше чисел)?

260. В кабинете физики имеется набор гирь: 100 г (одна штука), 50 г (1), 20 г (2), 10 г (1), 5 г (1), 2 г (2), 1 г (1). 1) Поясните, почему систему этих гирь можно считать системой счисления. 2) Укажите цифры и ключевые числа (базис) этой системы счисления. 3) Запишите в виде разложения по заданному базису 133 г, 209 г, 86 г. 4) Какие массы задаются числами 1121121, 10101, 1101100 этой системы?

261. Имеется набор монет достоинством 50 к. (2 монеты), 20 к. (2), 15 к. (3), 10 к. (4), 5 к. (3), 3 к. (2), 2 к. (4) и 1 к. (2). 1) Укажите цифры и базис этой системы. 2) В книжном магазине имеются книги, цена которых 2 р. 06 к., 1 р. 08 к., 67 к., 7 к. Запишите эти цены в заданном базисе (сначала используются монеты большего достоинства). 3) Сколько рублей и копеек соответствуют числам 333101, 40242, 10120110?

262. В системе летосчисления нашей эры базисом являются секунды, минуты, часы, сутки, месяцы, годы, века. 1) Укажите цифры каждого из 7 разрядов. 2) Запишите в таблицу этой системы счисления начало первого урока текущего учебного года.

263. В системе счисления "Час, сутки, неделя" запишите в таблице время, оставшееся: 1) до весенних каникул; 2) до нового года.