Не открывая кошельков

Фокусник высыпает на стол кучу монет на сумму 3 руб. и предлагает вам задачу: разложить деньги по 9 кошелькам так, чтобы можно было уплатить любую сумму до 3 руб., не открывая кошельков.

Это может показаться совершенно невыполнимым. Не думайте, однако, что фокусник расставил вам ловушку из игры слов или неожиданного их толкования. Посмотрите: фокусник сам берется за дело. Разложив монеты по кошелькам и привязав к каждому ярлычок с обозначением вложенной суммы, он предлагает вам назначить любую сумму не выше 3 руб.

Вы называете, например, 2 руб. 69 коп.

Без малейшего промедления фокусник отбирает и подает вам 4 кошелька. Вы открываете их и находите:

 в одном      - руб. 64 коп.
 в другом     - руб. 45 коп.
 в третьем    1 руб. 28 коп.
 в четвертом  - руб. 32 коп.
    Итого     2 руб. 69 коп.

Вы готовы заподозрить фокусника в ловкой подмене кошельков и требуете повторения фокуса. Он пододвигает все кошельки к вам, и когда вы называете новую сумму - например, 1 руб., или 7 коп., или 2 руб. 93 коп., - немедленно указывает, какие из лежащих кошельков должны вы взять, чтобы составилась назначенная вами сумма. А именно:

Для 1 руб. - 6 кошельков (32 коп., 1 коп., 45 коп., 16 коп., 2 коп., 4 коп.).

Для 7 коп. - 3 кошелька (1 коп., 2 коп., 4 коп.).

Для 2 р. 93 к. - 6 кошельков (128 коп., 32 коп., 8 коп., 45 коп., 64 коп., 16 коп.).

Фокус с 9 кошельками

Кошельки, по приказу фокусника, оказывается, всегда готовы составить любую названную сумму (до 3 руб.).

Чем это объяснить?

Секрет кроется в том, чтобы разложить монеты следующим образохм: 1 коп., 2 коп., 4 коп., 8 коп., 16 коп., 32 коп., 64 коп. и 128 коп. и, наконец, в последний - остальные деньги, то-есть

300 - (1 + 2 + 4 + 8 + 16 + 32 + 64 + 128) = 300 - 255 = 45 (коп.). 

Из первых 8 кошельков возможно, как нетрудно убедиться, составить любую сумму от 1 до 255 коп.; если же задается сумма большая, то пускают в дело последний кошелек, с 45 коп., а разницу составляют из первых 8 кошельков.

Вы можете проверить пригодность такой группировки чисел многочисленными пробами и убедиться, что из них можно действительно составить всякое число, не превышающее 300.

Но вас, вероятно, интересует и то, почему собственно ряд чисел 1, 2, 4, 8, 16, 32, 64 и т. д. обладает столь замечательным свойством. Это нетрудно понять, если вспомнить, что числа нашего ряда представляют степени 2: 2°, 2¹, 2², 2³, 2⁴ и т. д.^*, и, следовательно, их можно рассматривать как разряды двоичной системы счисления. А так как всякое число можно написать по двоичной системе, то, значит, и всякое число возможно составить из суммы степеней 2, то-есть из чисел ряда 1, 2, 4, 8, 16 и т. д. И когда вы подбираете кошельки, чтобы составить из их содержимого заданное число, вы, в сущности, выражаете заданное число в двоичной системе счисления. Например, число 100 легко составить, если изобразить его в двоичной системе:

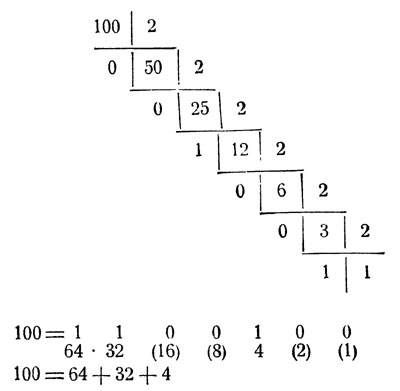
^* (Проходившие алгебру знают, что число 1 можно рассматривать, как 2 в нулевой степени.)

Напомним, что в двоичной системе на первом месте справа стоят единицы, на втором - двойки, на третьем - четверки, на четвертом - восьмерки и т. д.