Магические кольца

Что за странные кольца выставлены в следующей витрине нашей галереи? Перед нами три плоских кольца, вращающихся одно в другом.

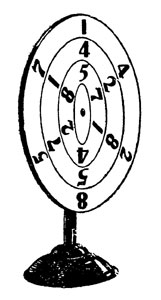
Вращающиеся числовые кольца

На каждом кольце написаны шесть цифр в одном и том же порядке, именно - обозначено число 142857. Кольца обладают следующим удивительным свойством: как бы ни были они повернуты, мы при сложении двух написанных на них чисел, считая от любой цифры в направлении часовой стрелки, получим во всех случаях шестизначное число (если только результат вообще будет шестизначный), лишь немного подвинутое! В том положении, например, какое изображено на прилагаемом чертеже, мы получаем при сложении двух наружных колец:

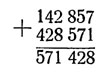
то-есть опять тот же ряд цифр: 142857, только цифры 5 и 7 перенеслись из конца в начало.

При другом расположении колец относительно друг друга имеем такие случаи:

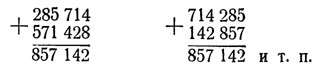
Исключение составляет случай, когда в результате получается 999999:

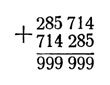
(Причину других отступлений от указанного правила читатель поймет, когда дочитает эту статью до конца.)

Мало того. Тот же ряд цифр в той же последовательности получим и при вычитании чисел, написанных на кольцах.

Например:

Исключение составляет случай, когда приведены к совпадению одинаковые цифры; тогда, разумеется, разность равна нолю.

Но и это еще не все. Умножьте число 142857 на 2, на 3, на 4, на 5 или на 6 - и вы получите снова то же число, лишь передвинутое, в круговом порядке, на одну или несколько цифр:

 142 857 X 2 = 285714, 
 142 857 X 3 = 428571, 
 142 857 X 4 = 571428, 
 142 857 X 5 = 714285, 
 142 857 X 6 = 857142. 

Чем же все загадочные особенности нашего числа обусловлены?

Мы нападем на путь к разгадке, если продлим немного последнюю табличку и попробуем умножить наше число на 7: в результате получится 999999. Значит, число 142857 не что иное, как седьмая часть 999999; и, следовательно, дробь 142857/999999 = 1/7. Действительно, если станете превращать 1/7 в десятичную дробь, вы получите:

Наше загадочное число есть период бесконечной периодической дроби, которая получается при превращении 1/7 в десятичную. Становится понятным теперь, почему при удвоении, утроении и т. д. этого числа происходит лишь перестановка одной группы цифр на другое место. Ведь умножение этого числа на 2 делает его равным 2/7 и, следовательно, равносильно превращению в десятичную дробь уже не 1/7, а 2/7. Начав же превращать дробь 2/7 в десятичную, вы сразу заметите, что цифра 2 - один из тех остатков, которые у нас уже получались при превращении 1/7; ясно, что должен повториться и прежний ряд цифр частного, но начнется он с другой цифры. Иными словами, должен получиться тот же период, но только несколько начальных цифр его очутятся на конце. То же самое произойдет и при умножении на 3, на 4, на 5 и на 6, то-есть на все числа, получающиеся в остатках. При умножении же на 7 мы должны получить единицу, или - что то же самое - 0,9999...

Любопытные результаты сложения и вычитания чисел на кольцах находят себе объяснение в том же факте, что 142 857 есть период дроби, равной 1/7. В самом деле: что мы собственно делаем, поворачивая кольцо на несколько цифр? Переставляем группу цифр с начала строки на конец, то-есть согласно только что сказанному умножаем число 142857 на 2, на 3, на 4 и т. д. Следовательно, все действия сложения или вычитания чисел, написанных на кольцах, сводятся к сложению или вычитанию дробей 1/7, 2/7, 3/7 и т. д. В результате мы должны получить, конечно, несколько седьмых долей, то-есть опять-таки наш ряд цифр 142857 в той или иной круговой перестановке. Отсюда надо исключить лишь случаи, когда складываются такие числа седьмых долей, которые в сумме дают единицу или больше 1.

Но и последние случаи исключаются не вполне: они дают результат, правда не тождественный с рассмотренными, но все же сходный с ними. Рассмотрим внимательнее, что должно получиться от умножения нашего загадочного числа на множитель больше 7, то-есть на 8, на 9 и т. д. Умножить 142857, например, на 8 мы можем так: умножить сначала на 7 и к произведению (то-есть к 999999) прибавить наше число:

142857 X 8 = 142857 X 7 + 142857 = 999999 + 142857 = 1000000 - 1 + 142 857 = 1000000 + (142857 - 1). 

Окончательный результат - 1142856 - отличается от умножаемого 142857 только тем, что впереди стоит еще одна единица, а последняя цифра на единицу же уменьшена. По сходному правилу составляются произведения 142857 на всякое другое число больше 7, как легко усмотреть из следующих строк:

 142857 Х  8 = (142857 Х 7)     + 142857       = 1142856, 
 142857 X  9 = (142857 X 7)     + (142857 X 2) = 1285713, 
 142857 X 10 = (142857 X 7)     + (142857 X 3) = 1428570, 
 142857 X 16 = (142857 X 7 X 2) + (142857 X 2) = 2285712, 
 142857 X 39 = (142857 X 7 X 5) + (142857 X 4) = 5571423. 

Общее правило здесь такое: при умножении 142 857 на любой множитель нужно умножить лишь на остаток от деления множителя на 7; впереди этого произведения ставится число, показывающее, сколько семерок в множителе, и то же число вычитается из результата^*. Пусть мы желаем умножить 142857 на 88. Множитель 88 при делении на 7 дает в частном 12 и в остатке 4. Следовательно, результат умножения таков:

12571428 - 12 = 12571416. 

^* (Если множитель кратен 7, то результат равен числу 999999, умноженному на число семерок в множителе; такое умножение легко выполнить в уме. Например, 142857 X 28 = 999999 X 4 = 4000000 - 4 = 3999996.)

От умножения 142857 на 365 мы получим (так как 365 при делении на 7 дает в частном 52, а в остатке 1):

52142857 - 52 = 52142805. 

Усвоив это простое правило и запомнив результаты умножения нашего диковинного числа на множители от 2 до 6 (что весьма нетрудно, нужно помнить лишь, с какой цифры они начинаются), вы можете изумлять непосвященных молниеносным умножением шестизначного числа. А чтобы не забыть этого удивительного числа, заметим, что оно произошло от 1/7, или, что то же самое, от 2/14; вот вам первые три цифры нашего числа: 142. Остальные три получаются вычитанием первых трех из 999:

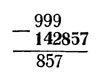
Мы уже имели дело с такими числами - именно, когда знакомились со свойствами числа 999. Вспомнив сказанное там, мы сразу сообразим, что число 142 857 есть, очевидно, результат умножения 143 на 999:

142857 = 143 X 999.

Но 143 = 13 X 11. Припомнив замеченное раньше о числе 1001, равном 7 Х 11 Х 13, мы будем в состоянии, не выполняя действия, предсказать, что должно получиться от умножения 142857 X 7:

142857 X 7 = 143 X 999 X 7 = 999 X 11 X 13 X 7 = = 999 X 1001 = 999999

(все эти преобразования мы, конечно, можем проделать в уме).

Чисел, подобных тому, с которым мы познакомились, существует множество. Они составляют словно одно семейство, так как объединены общим происхождением - от превращения простых дробей в бесконечные десятичные. Но не всякий период десятичной дроби обладает рассмотренным выше любопытным свойством давать при умножении круговую перестановку цифр. Не вдаваясь в тонкости теории, отметим, что это имеет место только для тех дробей, число цифр периода которых на единицу меньше знаменателя соответствующей простой дроби. Так, например:

  1/7 дает в периоде  6 цифр 
 1/17 дает в периоде 16 цифр 
 1/l9 дает в периоде 18 цифр 
 1/23 дает в периоде 22 цифр 
 1/29 дает в периоде 28 цифр 

Вы можете убедиться испытанием, что периоды дробей, получающихся от превращения 1/17, 1/19, 1/23 и 1/29 в десятичные, обладают теми же особенностями, как и рассмотренный нами период дроби 1/7.

Например, от 1/29 получаем число

0 344 827 586 206 896 551 724 137 931. 

Если указанное сейчас условие (относительно чисел цифр периода) не соблюдено, то соответствующий период дает число, не принадлежащее к занимающей нас семье интересных чисел. Например, 1/13 дает десятичную дробь с шестью (а не с 12) цифрами в периоде:

1/13 = 0,076923.

Помножив на 2, получаем совершенно иное число:

2/13 = 0,153846.

Почему? Потому что среди остатков от деления 1:13 не было числа 2. Различных остатков было столько, сколько цифр в периоде, то-есть 6; различных же множителей для дроби 1/13 у нас 12; следовательно, не все множители будут среди остатков, а только 6. Легко убедиться, что эти множители следующие: 1, 3, 4, 9, 10, 12. Умножение на эти 6 чисел дает круговую перестановку (076923 X 3 = 230769), на остальные - нет. Вот почему от 1/13 получается число, лишь отчасти пригодное для "магического кольца". То же надо сказать и о ряде других периодов.

Каждая сумма состоит только из девяти разных цифр.