Мудрый обычай старины

Добравшись после утомительных трудов до желанного конца арифметического действия, предки наши считали необходимым непременно проверить этот в поте лица добытый итог. Громоздкие приемы вызывали недоверие к их результатам. На длинном, извилистом пути легче заблудиться, чем на прямой дороге современных приемов. Отсюда естественно возник старинный обычай проверять каждое выполняемое арифметическое действие - похвальное правило, которому не мешало бы и нам следовать.

Любимым приемом проверки был так называемый "способ девятки". Этот изящный прием нередко описывается и в современных арифметических учебниках, особенно иностранных.

Проверка девяткой основана на "правиле остатков", гласящем: остаток от деления суммы на какое-либо число равен сумме остатков от деления каждого слагаемого на то же число. Точно так же остаток произведения равен произведению остатков множителей. С другой стороны, известно также^*, что при делении числа на 9 получается тот же остаток, что и при делении на 9 суммы цифр этого числа; например, 758 при делении на 9 дает остаток 2, и то же получается в остатке от деления (7 + 5 + 8) на 9. Сопоставив оба указанных свойства, мы и приходим к приему проверки девяткой, то-есть с делением на 9. Покажем на примере.

^* (Выясняется попутно при выводе признака делимости на 9.)

Пусть требуется проверить правильность сложения следующего столбца:

Составляем в уме сумму цифр каждого слагаемого, причем в получающихся попутно двузначных числах также складываем цифры (делается это в самом процессе сложения цифр), пока, в конечном результате, не получим однозначного числа. Результаты эти (остатки от деления на 9) записываем, как показано на примере, рядом с соответствующим слагаемым. Складываем все остатки (7 + 7 + 1 + 2 = 17; 1 + 7 = 8), получаем 8. Такова же должна быть сумма цифр итога (5339177), если действие выполнено верно: 5 + 3 + 3 + 9 + 1 + + 7 + 7 после всех упрощений равно 8.

Проверка вычитания выполняется точно так же, если принять уменьшаемое за сумму, а вычитаемое и разность - за слагаемые. Например:

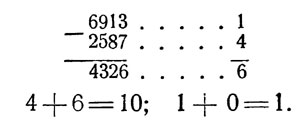
Особенно удобен этот прием в применении к проверке действия умножения, как видно из следующего примера:

Если при такой проверке умножения обнаружена будет ошибочность результата, то, чтобы определить, где именно кроется ошибка, можно проверить способом девятки каждое частное произведение отдельно; а если здесь ошибки не окажется, остается проверить лишь сложение частных произведений.

Как по этому способу проверять деление? Если у нас случай деления без остатка, то делимое рассматривается как произведение делителя на частное. В случае же деления с остатком пользуются тем, что делимое=делителю X частное + остаток.

Например:

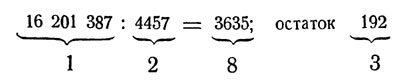
сумма цифр:

2 X 8 + 3 = 19; 1 + 9 = 10; 1 + 0 = 1.

Привожу из "Арифметики" Магницкого предлагаемое там для проверки девяткой удобное расположение:

Для умножения:

Для деления:

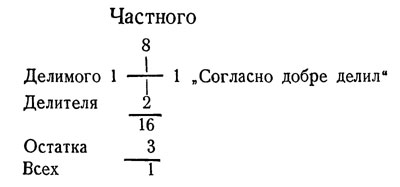
Подобная проверка действий, без сомнения, не оставляет желать лучшей в смысле быстроты и удобства. Нельзя сказать того же о ее надежности: ошибка может и ускользнуть от нее. Действительно, одну и ту же сумму цифр могут иметь разные числа; не только перестановка цифр, но, иной раз, даже и замена одних другими остаются при такой проверке необнаруженными. Укрываются от контроля также лишние девятки и нули, потому что не влияют на сумму цифр. Всецело полагаться поэтому на такой прием проверки было бы неосмотрительно. Предки наши сознавали это и не ограничивались одной лишь проверкой с помощью девятки, но производили еще дополнительную проверку - чаще всего с помощью семерки. Этот прием основан на том же "правиле остатков", но не так удобен, как способ девятки, потому что деление на 7 приходится выполнять полностью, чтобы найти остатки (а при этом легко возможны ошибки в действиях самой проверки).

Две проверки - девяткой и семеркой - являются уже гораздо более надежным контролем: что ускользнет от одной, будет уловлено другой. Ошибка не обнаружится лишь в том случае, если разность истинного и полученного результатов кратная числу 7 X 9 = 63. Так как подобная случайность все же возможна, то и двойная проверка не дает полной уверенности в правильности результата.

Впрочем, для обычных вычислений, где ошибаются чаще всего на одну или две единицы, можно ограничиться только проверкой девяткой. Дополнительная проверка семеркой чересчур обременительна. Только тот контроль хорош, который не мешает работе.

Если тем не менее, выполняя ответственное вычисление, вы пожелаете для надежности произвести двойную проверку, то вместо делителя 7 лучше пользоваться делителем 11. При этом дело можно значительно упростить, применив следующий удобный признак делимости на 11: число разбивают на грани справа налево, по две цифры в каждой (самая левая грань может заключать и одну цифру); грани складывают, и полученная сумма будет "равноостаточна" с испытуемым числом по делителю 11: сумма граней дает при делении на 11 тот же остаток, что и испытуемое число.

Поясним сказанное примером. Требуется найти остаток от деления 24 716 на 11. Разбиваем число на грани и складываем их:

 2 + 47 + 16 = 65. 
       46 

Так как 65 при делении на 11 дает в остатке 10, то и число 24 716 дает при делении на 11 тот же остаток.

Я предлагаю этот способ потому, что он одновременно дает и число, равноостаточное с испытуемым также по делителю 9. Таким образом, мы имеем возможность удобно произвести проверку сразу посредством двух делителей: 9 и 11. От такой проверки может ускользнуть только ошибка, кратная 99, то-есть весьма маловероятная.