Глава вторая. Потомок Древнего Абака

Чеховская головоломка

Потомок Древнего Абака

Припомним ту, в своем роде знаменитую, арифметическую задачу, которая так смутила некогда семиклассника Зиберова из чеховского рассказа "Репетитор".

"Купец купил 138 арш.* черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.?"

^* (Аршин - русская мера длины, равная 0,711 м.)

С тонким юмором описывает Чехов, как беспомощно трудились над этой задачей и семиклассник-репетитор и его ученик, 12-летний Петя, пока не выручил их Петин отец, Удодов:

"Петя повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138.

- Для чего же вы делите? Постойте! Впрочем, так... продолжайте. Остаток получается? Здесь не может быть остатка. Дайте-ка, я разделю!

Зиберов (репетитор. - Я. П.) делит, получает 3 с остатком и быстро стирает.

" Странно... - думает он, ероша волосы и краснея.- Как же она решается? Гм!.. Это задача на неопределенные уравнения, а вовсе не арифметическая".

Учитель глядит в ответы и видит 75 и 63.

" Гм!.. странно... Сложить 5 и 3, а потом делить 540 на 8? Так, что ли? Нет, не то".

- Решайте же! - говорит он Пете.

- Ну, чего думаешь? Задача-то ведь пустяковая! - говорит Удодов Пете.-Экий ты дурак, братец! Решите уж вы ему, Егор Алексеич.

Егор Алексеич (репетитор. - Я. П.) берет в руки грифель и начинает решать. Он заикается, краснеет, бледнеет.

- Эта задача, собственно говоря, алгебраическая, - говорит он. - Ее с иксом и игреком решить можно. Впрочем, можно и так решить. Я вот разделил... понимаете? Теперь вот надо вычесть... понимаете? Или вот что... Решите мне эту задачу к завтраму... Подумайте..

Петя ехидно улыбается. Удодов тоже улыбается. Оба они понимают замешательство учителя. Ученик VII класса еще пуще конфузится, встает и начинает ходить из угла в угол.

Русские конторские счеты

- И без алгебры решить можно, - говорит Удодов, протягивая руку к счетам и вздыхая. - Вот, извольте видеть...

Он щелкает на счетах, и у него получается 75 и 63, что и нужно было.

- Вот-с... по-нашему, по-неученому".

Эта история с задачей, заставляющая нас смеяться над конфузом злосчастного репетитора, задает нам сама три новые задачи. А именно:

1. Как намеревался репетитор решить задачу алгебраически?
2. Как должен был решить ее Петя?
3. Как решил ее отец Пети на счетах "по-неученому"?

На первые два вопроса, вероятно, без труда ответят если не все, то весьма многие читатели нашей книжки. Третий вопрос не так прост. Но рассмотрим их по порядку.

1. Семиклассник-репетитор готов был решать задачу "с иксом и игреком", будучи уверен, что задача - "собственно говоря, алгебраическая". И он, надо думать, легко справился бы с ней, прибегнув к помощи системы уравнений (только не неопределенных, как ему казалось). Составить два уравнения с двумя неизвестными для данной задачи очень нетрудно; вот они:

х + y = 138; 5х + 3y = 540,

где х - число аршин синего, а y - черного сукна.

2. Однако задача легко решается и арифметически. Если бы вам пришлось решать ее, вы начали бы с предположения, что все купленное сукно было синее, тогда за партию в 138 аршин синего сукна пришлось бы уплатить 5 X 138 = 690 руб.; это на 690 - 540 = 150 руб. больше того, что было заплачено в действительности^*. Разница в 150 руб. указывает, что в партии имелось и более дешевое, черное сукно - по 3 руб. аршин. Дешевого сукна было столько, что из двух рублей разницы на каждом аршине составилось 150 руб.: очевидно, число аршин черного сукна определится, если разделить 150 на 2. Получаем ответ - 75; вычтя эти 75 аршин из общего числа 138 аршин, узнаем, сколько было синего сукна: 138 - 75 = 63. Так и должен был решать задачу Петя.

^* (Можно начинать с предположения, что все купленное сукно было черное. Предоставляем это сделать самому читателю. - Ред.)

3. На очереди третий вопрос: как решил задачу Удодов-старший?

В рассказе говорится очень кратко: "Он щелкает на счетах, и у него получается 75 и 63, что и нужно было".

В чем, однако, состояло это "щелканье на счетах"?

Каков способ решения задачи с помощью счетов?

Разгадка такова: злополучная задача решается на счетах тем же приемом, что и на бумаге, - теми же арифметическими действиями. Но выполнение их упрощается благодаря преимуществам, которые наши русские счеты предоставляют всякому, умеющему с ними обращаться. Очевидно, "отставной губернский секретарь" Удодов хорошо умел считать на счетах, потому что их косточки быстро, без помощи алгебры, открыли ему то, чего репетитор-семиклассник добивался узнать "с иксом и игреком". Проследим же, какие действия должен был проделать на счетах Петин отец.

Прежде всего ему нужно было, как мы знаем, умножить 138 на 5. Для этого он, по правилам действий на счетах, умножил сначала 138 на 10, то-есть просто перенес 138 одним рядом выше, а затем разделил это число пополам опять-таки на счетах же. Деление начинают снизу: откидывают половину косточек, отложенных на каждой проволоке; если число косточек на данной проволоке нечетное, то выходят из затруднения, "раздробляя" одну косточку этой проволоки на 10 нижних.

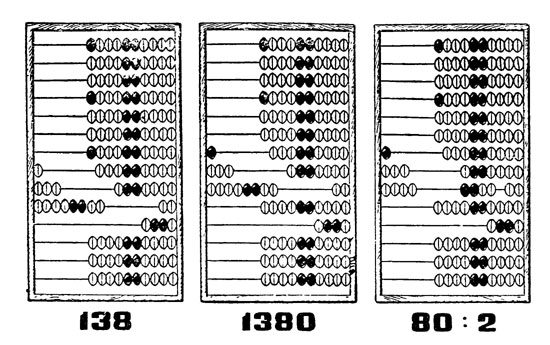
Чтобы умножить 138 на 5 при помощи конторских счетов, поступают так: сначала на счетах откладывают 138; затем простым переносом отложенных косточек на один ряд вверх число 138 множится на 10; после этого его делят на 2 (десятки уже разделены), и таким образом получают результат 138 X 5

В нашем, например, случае делят 1380 пополам так: на нижней проволоке, где отложено 8 косточек, откидывают 4 косточки (4 десятка), на средней проволоке из 3 косточек откидывают 1, а из оставшихся 2 косточек 1 заменяют мысленно 10 нижними и делят пополам, добавляя 5 десятков к косточкам нижней; на верхней проволоке раздробляют 1 косточку, прибавляя 5 сотен к косточкам средней проволоки. В результате на верхней проволоке совсем не остается косточек; на средней 1 + 5 = 6 сотен, на нижней 4 + 5 = 9 десятков. Итого 690 единиц. Выполняется все это быстро, автоматически.

Далее Удодову-старшему нужно было из 690 вычесть 540. Как проделывается это на счетах, всем известно.

Наконец полученную разность, 150, оставалось разделить пополам: Удодов откинул из 5 косточек (десятков) 3, отдав 5 единиц нижнему ряду косточек; потом из 1 косточки на проволоке сотен отдал 5 десятков нижнему ряду: получилось 7 десятков и 5 единиц, то-есть 75.

Все эти простые действия выполняются на счетах, конечно, гораздо скорее, чем тут описано.