Громкоговорители

Задача

На площади установлено 5 громкоговорителей, разбитых на две группы: в одной 2, в другой 3 аппарата. Расстояние между группами 50 м. Где надо стать, чтобы звуки обеих групп доносились с одинаковой силой?

Решение

Если расстояние искомой точки от меньшей группы обозначим через х, то расстояние ее от большей группы выразится через 50 - x (рис. 16). Зная, что сила звука ослабевает пропорционально квадрату расстояния, имеем уравнение

2/3 = x2/(50 - x)2

которое после упрощения приводится к виду

х2 + 200x - 5000 = 0,

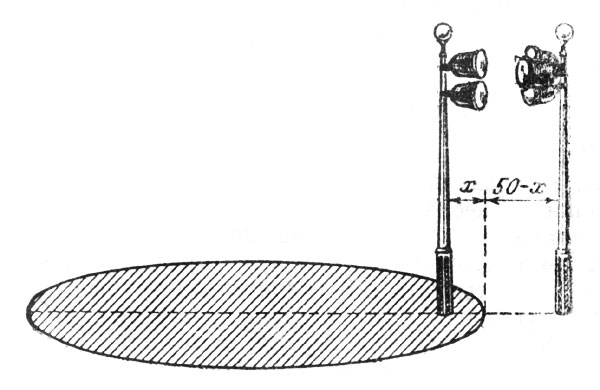
Рис. 16. Если расстояние искомой точки от меньшей группы обозначим через х, то расстояние ее от большей группы выразится через 50 - x

Решив его, получаем два корня:

x1 = 22,5, 
х2 = -222,5.

Положительный корень прямо отвечает на вопрос задачи: точка равной слышимости расположена в 22,5 м от группы из двух громкоговорителей и, следовательно, в 27,5 м от группы трех аппаратов.

Но что означает отрицательный корень уравнения? Имеет ли он смысл?

Безусловно. Знак минус означает, что вторая точка равной слышимости лежит в направлении, противоположном тому, которое принято было за положительное при составлении уравнения.

Отложив от местонахождения двух аппаратов в требуемом направлении 222,5 м, найдем точку, куда звуки обеих групп громкоговорителей доносятся с одинаковой силой. От группы из трех аппаратов точка эта отстоит в 222,5 м + 50 м = 272,5 м.

Итак, нами разысканы две точки равной слышимости - из тех, что лежат на прямой, соединяющей источники звука. Других таких точек на этой линии нет, но они имеются вне ее. Можно доказать, что геометрическое место точек, удовлетворяющих требованию нашей задачи, есть окружность, проведенная через обе сейчас найденные точки, как через концы диаметра. Окружность эта ограничивает, как видим, довольно обширный участок (заштрихованный на чертеже), внутри которого слышимость группы двух громкоговорителей пересиливает слышимость группы трех аппаратов, а за пределами этого круга наблюдается обратное явление.