
Продажа кур
Старинная задача
Три сестры пришли на рынок с курами. Одна принесла для продажи 10 кур, другая 16, третья 26. До полудня они продали часть своих кур по одной и той же цене. После полудня, опасаясь, что не все куры будут проданы, они понизили цену и распродали оставшихся кур снова по одинаковой цене. Домой все трое вернулись с одинаковой выручкой: каждая сестра получила от продажи 35 рублей.
По какой цене продавали они кур до и после полудня?
Решение
Обозначим число кур, проданных каждой сестрой до полудня, через х, у, z. Во вторую половину дня они продали 10 - х, 16 - у, 26 - z кур. Цену до полудня обозначим через m, после полудня - через n. Для ясности сопоставим эти обозначения:
| Число проданных кур | Цена | |||
| До полудня | x | y | z | m |
| После полудня | 10 - x | 16 - y | 26 - z | n |
Первая сестра выручила:
mх + n(10 - х); следовательно, mx + n(10 - x) = 35;
вторая:
mу + n(16 - у); следовательно, mу + n(16 - y) = 35;
третья:
mz + n(26 - z); следовательно, mz + n(26 - z) = 35.
Преобразуем эти три уравнения:
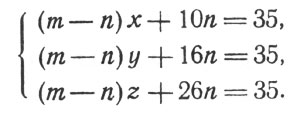
Вычтя из третьего уравнения первое, затем второе, получим последовательно:
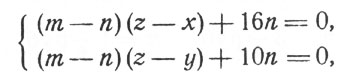
или
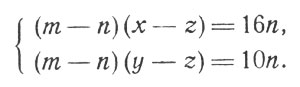
Делим первое из этих уравнений на второе:
(x - z)/(у - z) = 8/5, или (x - z)/8 = (y - z)/5.
Так как х, у, z - числа целые, то и разности x - z, у - z - тоже целые числа. Поэтому для существования равенства
(x - z)/8 = (y - z)/5
необходимо, чтобы x - z делилось на 8, a y - z на 5.
Следовательно,
(x - z)/8 = t = (y - z)/5,
откуда
x = z + 8t, у = z + 5t.
Заметим, что число t - не только целое, но и положительное, так как x > z (в противном случае первая сестра не могла бы выручить столько же, сколько третья).
Так как x < 10, то
z + 8t < 10.
При целых и положительных z и t последнее неравенство удовлетворяется только в одном случае: когда z = 1 и t = 1. Подставив эти значения в уравнения
x = z + 8t и y = z + 5t,
находим: х = 9, у = 6.
Теперь, обращаясь к уравнениям
mх + n(10 - х) = 35, mу + n(16 - y) = 35, mz + n(26 - z) = 35
и подставив в них найденные значения x, y, z, узнаем цены, по каким продавались куры:
m = 3 3/4 руб., n = 1 1/4 руб.
Итак, куры продавались до полудня по 3 руб. 75 коп., после полудня по 1 руб. 25 коп.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'