Быстродействующие вычислительные машины

Беседа об уравнениях в плане "Занимательной алгебры" не может пройти мимо решения уравнений на вычислительных машинах. Мы уже говорили о том, что вычислительные машины могут "играть" в шахматы (или шашки). Математические машины могут выполнять и другие задания, например, перевод с одного языка на другой, оркестровку музыкальной мелодии и т.д. Нужно только разработать соответствующую "программу", по которой машина будет действовать.

Конечно, мы не будем рассматривать здесь "программы" для игры в шахматы или для перевода с одного языка на другой: эти "программы" крайне сложны. Мы разберем лишь две очень простенькие "программы". Однако вначале нужно сказать несколько слов об устройстве вычислительной машины.

Выше (в гл. I) мы говорили об устройствах, которые позволяют производить многие тысячи вычислений в секунду. Эта часть вычислительной машины, служащая для непосредственного выполнения действий, называется арифметическим устройством. Кроме того, машина содержит управляющее устройство (регулирующее работу всей машины) и так называемую память. Память, или, иначе, запоминающее устройство, представляет собой хранилище для чисел и условных сигналов. Наконец, машина снабжена особыми устройствами для ввода новых цифровых данных и для выдачи готовых результатов. Эти готовые результаты машина печатает (уже в десятичной системе) на специальных карточках.

Всем хорошо известно, что звук можно записать на пластинку или на пленку и затем воспроизвести. Но запись звука на пластинку может быть произвел дена лишь один раз: для новой записи нужна уже новая пластинка. Несколько иначе осуществляется запись звука в магнитофоне: при помощи намагничивания особой ленты. Записанный звук можно воспроизвести нужное число раз, а если запись оказалась уже ненужной, ее можно "стереть" и произвести на той же ленте новую запись. На одной и той же ленте можно произвести одну за другой несколько записей, причем при каждой новой записи предыдущая "стирается".

На подобном же принципе основано действие запоминающих устройств. Числа и условные сигналы записываются (при помощи электрических, магнитных или механических сигналов) на специальном барабане, ленте или другом устройстве. В нужный момент записанное число может быть "прочтено", а если оно уже больше не нужно, то его можно стереть, а на его месте записать другое число. "Запоминание" и "чтение" числа или условного сигнала длятся всего лишь миллионные доли секунды.

"Память" может содержать несколько тысяч ячеек, каждая ячейка - несколько десятков элементов, например магнитных. Для записи чисел по двоичной системе счисления условимся считать, что каждый намагниченный элемент изображает цифру 1, а ненамагниченный - цифру 0. Пусть, например, каждая ячейка памяти содержит 25 элементов (или, как говорят, 25 "двоичных разрядов", причем первый элемент ячейки служит для обозначения знака числа (+ или -), следующие 14 разрядов служат для записи целой части числа, а последние 10 разрядов - для записи дробной части. На рис. 11 схематически изображены две ячейки памяти; в каждой по 25 разрядов. Намагниченные элементы обозначены знаком +, ненамагниченные обозначены знаком -. Рассмотрим верхнюю из изображенных ячеек (запятая показывает, где начинается дробная часть числа, а пунктирная линия отделяет первый разряд, служащий для записи знака, от остальных). В ней записано (вдвоичной системе счисления) число +1011,01 или - в привычной для нас десятичной системе счисления - число 11,25.

Кроме чисел в ячейках памяти записываются приказы, из которых состоит программа. Рассмотрим, как выглядят приказы для так называемой трех-адресной машины. В этом случае при записи приказа ячейка памяти разбивается на 4 части (пунктирные линии на нижней ячейке, рис. 11). Первая часть служит для обозначения операции, причем операции записываются числами (номерами).

Например,

 сложение -  операция 1, 
 вычитание - операция 2, 
 умножение - операция 3 и т. д.

Приказы расшифровываются так: первая часть ячейки - номер операции, вторая и третья части - номера ячеек (адреса), из которых надо взять числа для выполнения этой операции, четвертая часть - номер ячейки (адрес), куда следует отправить полученный результат. Например, на рис. 11 (нижняя строка) записаны в двоичной системе числа 11, 11, 111, 1011 или в десятичной системе: 3, 3, 7, 11, что означает следующий приказ: выполнить операцию 3 (т. е. умножение) над числами, находящимися в третьей и седьмой ячейках памяти, а полученный результат "запомнить" (т. е. записать) в одиннадцатой ячейке.

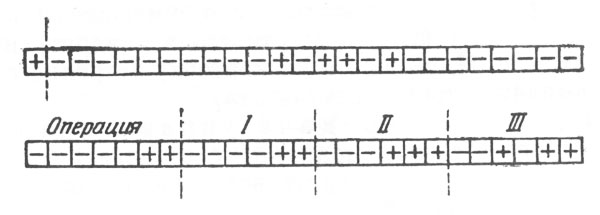
Рис. 11. Записаны в двоичной системе числа 11, 11, 111, 1011

В дальнейшем мы будем записывать числа и приказы не условными значками, как на рис. 11, а прямо в десятичной системе счисления. Например, приказ, изображенный в нижней строке рис. 11, запишется так:

умножение 3 7 11

Рассмотрим теперь два простеньких примера программ.

 Программа 1 
 1) сложение  4 5 4 
 2) умножение 4 4 → 
 3) п. у.       1 
 4) 0 
 5) 1 

Посмотрим, как будет работать машина, у которой в первых пяти ячейках записаны эти данные.

1-й приказ: сложить числа, записанные в 4-й и 5-й ячейках, и отправить результат снова в 4-ю ячейку (вместо того, что там было записано ранее). Таким образом, машина запишет в 4-ю ячейку число 0+1 = 1. После выполнения 1-го приказа в 4-й и 5-й ячейках будут следующие числа:

 4) 1 
 5) 1. 

2-й приказ: умножить число, имеющееся в 4-й ячейке, на себя (т. е. возвести его в квадрат) и результат, т. е. 1², выписать на карточку (стрелка означает выдачу готового результата).

3-й приказ: передача управления в 1-ю ячейку. Иначе говоря, приказ п. у. означает, что надо снова по порядку выполнять все приказы, начиная с 1-го. Итак, снова 1-й приказ.

1-й приказ: сложить числа, имеющиеся в 4-й и 5-й ячейках, и результат снова записать в 4-й ячейке. В результате в 4-й ячейке будет число 1 + 1 =2:

 4) 2, 
 5) 1.

2-й приказ: возвысить в квадрат число, стоящее в 4-й ячейке, и полученный результат, т. е. 2², выписать на карточку (стрелка - выдача результата).

3-й приказ: передача управления в первую ячейку (т. е. опять переход к 1-му приказу).

1-й приказ: число 2 + 1 = 3 отправить в 4-ю ячейку:

 4) 3, 
 5) 1. 

2-й приказ: выписать на карточку число 3².

3-й приказ: передача управления в 1-ю ячейку и т. д.

Мы видим, что машина вычисляет один за другим квадраты целых чисел и выписывает их на карточку. Заметьте, что каждый раз набирать новое число вручную не надо: машина сама перебирает подряд целые числа и возводит их в квадрат. Действуя по этой программе, машина вычислит квадраты всех целых чисел, скажем, от 1 до 10000 в течение нескольких секунд (или даже долей секунды).

Следует отметить, что в действительности программа для вычисления квадратов целых чисел должна быть несколько сложнее той, которая приведена выше. Это прежде всего относится ко 2-му приказу. Дело в том, что выписывание готового результата на карточку требует во много раз больше времени, чем выполнение машиной одной операции. Поэтому готовые результаты сначала "запоминаются" в свободных ячейках "памяти", а уже после этого ("не спеша") выписываются на карточку. Таким образом, первый окончательный результат должен "запоминаться" в 1-й свободной ячейке "памяти", второй результат - во 2-й свободной ячейке, третий - в 3-й и т. д. В приведенной выше упрощенной программе это никак не было учтено.

Кроме того, машина не может долго заниматься вычислением квадратов - не хватит ячеек "памяти", - а "угадать", когда машина уже вычислила нужное нам число квадратов, чтобы в этот момент выключить ее, - невозможно (ведь машина производит многие тысячи операций в секунду!). Поэтому предусмотрены особые приказы для остановки машины в нужный момент. Например, программа может быть составлена таким образом, что машина вычислит квадраты всех целых чисел от 1 до 10000 и после этого автоматически выключится.

Есть и другие более сложные виды приказов, на которых мы здесь для простоты не останавливаемся.

Вот как выглядит в действительности программа для вычисления квадратов всех целых чисел от 1 до 10000:

 Программа 1а
 1) сложение  8 9  8
 2) умножение 8 8 10
 3) сложение  2 6  2
 4) у. п. у.  8 7  1
 5) стоп
 6)           0 0  1
 7) 10000
 8)  0 
 9)  1 
 10) 0 
 11) 0 
 12) 0 
 ...................

Первые два приказа мало отличаются от тех, которые были в предыдущей упрощенной программе. После выполнения этих двух приказов в 8-й, 9-й и 10-й ячейках будут следующие числа:

 8) 1 
 9) 1 
10) 12

Третий приказ очень интересен: надо сложить то, что стоит во 2-й и 6-й ячейках, и результаты снова записать во 2-й ячейке, после чего 2-я ячейка будет иметь вид

2) умножение 8 8 11.

Как видите, после выполнения третьего приказа меняется второй приказ, вернее меняется один из адресов 2-го приказа. Ниже мы выясним, для чего это делается.

Четвертый приказ: условная передача управления (вместо 3-го приказа в рассмотренной ранее программе). Этот приказ выполняется так: если число, стоящее в 8-й ячейке, меньше числа, стоящего в 7-й ячейке, то передается управление в 1-ю ячейку; в противном случае выполняется следующий (т. е. 5-й) приказ. В нашем случае действительно 1 < 10000, так что происходит передача управления в 1-ю ячейку. Итак, снова 1-й приказ.

После выполнения 1-го приказа в 8-й ячейке будет число 2.

Второй приказ, который теперь имеет вид

2) умножение 8 8 11,

заключается в том, что число 2² направляется в 11-ю ячейку. Теперь ясно, зачем был выполнен ранее 3-й приказ: новое число, т. е. 2², должно попасть не в 10-ю ячейку, которая уже занята, а в следующую.

После выполнения 1-го и 2-го приказов у нас будет следующие числа:

  8) 2 
  9) 1 
 10) 12 
 11) 22

После выполнения 3-го приказа 2-я ячейка примет вид

2) умножение 8 8 12,

т. е. машина "подготовилась" к тому, чтобы записать новый результат в следующую, 12-ю ячейку. Так как в 8-й ячейке все еще стоит меньшее число, чем в 9-й ячейке, то 4-й приказ означает снова передачу управления в 1-ю ячейку.

Теперь после выполнения 1-го и 2-го приказов получим:

  8) 3 
  9) 1 
 10) 12 
 11) 22 
 12) 32 

До каких пор машина будет по этой программе вычислять квадраты? До тех пор, пока в 8-й ячейке не появится число 10000, т. е. пока не будут вычислены квадраты чисел от 1 до 10000. После этого 4-й приказ уже не передаст управления в 1-ю ячейку (так как в 8-й ячейке будет стоять число, не меньшее, а равное числу, стоящему в 7-й ячейке), т. е. после 4-го приказа машина выполнит 5-й приказ: остановится (выключится).

Рассмотрим теперь более сложный пример программы: решение систем уравнений. При этом мы рассмотрим упрощенную программу. При желании читатель сам подумает о том, как должна выглядеть такая программа в полном виде.

Пусть задана система уравнений

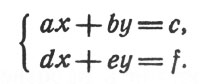
Эту систему нетрудно решить:

x = (ce - bf)/(ae - bd),  y = (af - cd)/(ae - bd).

Для решения такой системы (с заданными числовыми значениями коэффициентов а, b, с, d, е, f) вам потребуется, вероятно, несколько десятков секунд. Машина же может решить в секунду тысячи таких систем.

Рассмотрим соответствующую программу. Будем считать, что даны сразу несколько систем:

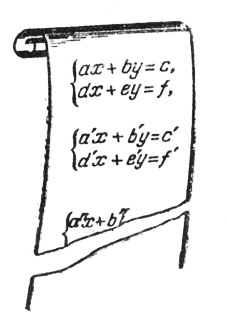
Даны сразу несколько систем

с числовыми значениями коэффициентов а, Ь, с, d, е, f, а', b', ...

Вот соответствующая программа:

  Программа 2
                                           26) a
 1) × 28 30 20      14) +    3 19 3   27) b
 2) × 27 31 21      15) +    4 19 4   28) c
 3) × 26 30 22      16) +    5 19 5   29) d
 4) × 27 29 23      17) +    6 19 6   30) e
 5) × 26 31 24      18) п. у.     1   31) f
 6) × 28 29 25      19)      6  6 0   32) a'
 7)     -  20 21 20      20)      0        33) b'
 8)     -  22 23 21      21)      0        34) c'
 9)     -  24 25 22      22)      0        35) d'
10)     :  20 21 → 23)      0        36) e'
11)     :  22 21 → 24)      0        37) f'
12)     +   1 19 1       25)      0        38) a''
13)     +   2 19 2

1-й приказ: составить произведение чисел, стоящих в 28-й и 30-й ячейках, и направить результат в 20-ю ячейку. Иначе говоря, в 20-й ячейке будет записано число ce.

Аналогично выполняются приказы 2-й - 6-й. После их выполнения в ячейках 20-й - 25-й будут находиться следующие числа:

 20) се 
 21) bf 
 22) ае 
 23) bd 
 24) af 
 25) cd

7-й приказ: из числа, стоящего в 20-й ячейке, вычесть число, стоящее в 21-й ячейке, и результат (т. е. се - bf) снова записать в 20-ю ячейку.

Аналогично выполняются приказы 8-й и 9-й. В результате в ячейках 20-й, 21-й, 22-й окажутся следующие числа:

 20) се - bf 
 21) ae - bd 
 22) af - cd 

10-й и 11-й приказы: составляются частные

(се - bf)/(ae - bd) и (af - cd)/(ae - bd)

и выписываются на карточку (т. е. выдаются как готовые результаты). Это и есть значения неизвестных, получаемых из первой системы уравнений.

Итак, первая система решена. Зачем же дальнейшие приказы? Дальнейшая часть программы (ячейки 12-я - 19-я) предназначена для того, чтобы заставить машину "подготовиться" к решению второй системы уравнений. Посмотрим, как это происходит. Приказы с 10-го по 17-й заключаются в том, что к содержимому ячеек 1-й - 6-й прибавляется запись, имеющаяся в 19-й ячейке, а результаты снова остаются в ячейках 1-й - 6-й. Таким образом, после выполнения 17-го приказа первые шесть ячеек будут иметь следующий вид:

1) × 34 36 20
2) × 33 37 21
3) × 32 36 22
4) × 33 35 23
5) × 32 37 24
6) × 34 35 25

18-й приказ: передача управления в первую ячейку.

Чем же отличаются новые записи в первых шести ячейках от прежних записей? Тем, что первые два адреса в этих ячейках имеют номера не от 26 до 31, как прежде, а номера от 32 до 37. Иначе говоря, машина снова будет производить те же действия, но числа будет брать не из ячеек 26-й - 31-й, а из ячеек 32-й - 37-й, где стоят коэффициенты второй системы уравнений. В результате машина решит вторую систему уравнений. После решения второй системы машина перейдет к третьей и т. д.

Из сказанного становится ясным, как важно уметь составить правильную "программу". Ведь машина "сама" ничего делать не "умеет". Она может лишь выполнять заданную ей программу. Имеются программы для вычисления корней, логарифмов, синусов, для решения уравнений высших степеней и т. д. Мы уже говорили выше о том, что существуют программы для игры в шахматы, для перевода с иностранного языка, ... Конечно, чем сложнее задание, тем сложнее соответствующая программа.

Заметим в заключение, что существуют так называемые программирующие программы, т. е. такие, с помощью которых сама машина может составить требуемую для решения задачи программу. Это значительно облегчает составление программы, которое часто бывает очень трудоемким.