Курьезы и неожиданности

При решении уравнений мы наталкиваемся иногда на ответы, которые могут поставить в тупик малоопытного математика. Приведем несколько примеров.

I. Найти двузначное число, обладающее следующими свойствами. Цифра десятков на 4 меньше цифры единиц. Если из числа, записанного теми же цифрами, но в обратном порядке, вычесть искомое число, то получится 27.

Обозначив цифру десятков через х, а цифру единиц - через у, мы легко составим систему уравнений для этой задачи:

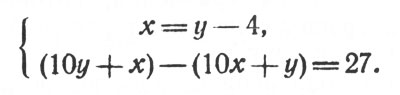
Подставив во второе уравнение значение х из первого, найдем:

10y + у - 4 - [10(у-4) + y] = 27,

а после преобразований:

36 = 27.

У нас не определились значения неизвестных, зато мы узнали, что 36 = 27... Что это значит?

Это означает лишь, что двузначного числа, удовлетворяющего поставленным условиям, не существует

и что составленные уравнения противоречат одно другому.

В самом деле: умножив обе части первого уравнения на 9, мы найдем из него:

9у - 9x = 36,

а из второго (после раскрытия скобок и приведения подобных членов):

9у - 9х = 27.

Одна и та же величина 9у - 9х согласно первому уравнению равна 36, а согласно второму 27. Это безусловно невозможно, так как 36 ≠ 27.

Подобное же недоразумение ожидает решающего следующую систему уравнений:

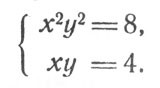
Разделив первое уравнение на второе, получаем:

ху = 2,

а сопоставляя полученное уравнение со вторым, видим, что

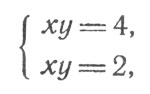
т. е. 4 = 2. Чисел, удовлетворяющих этой системе, не существует. (Системы уравнений, которые, подобно сейчас рассмотренным, не имеют решений, называются несовместными.)

II. С иного рода неожиданностью встретимся мы, если несколько изменим условие предыдущей задачи. Именно будем считать, что цифра десятков не на 4, а на 3 меньше, чем цифра единиц, а в остальном оставим условие задачи тем же. Что это за число?

Составляем уравнение. Если цифру десятков обозначим через х, то число единиц выразится через х + 3. Переводя задачу на язык алгебры, получим:

10(x + 3) + x - [10x + (x + 3)] = 27. 

Сделав упрощения, приходим к равенству

27 = 27.

Это равенство неоспоримо верно, но оно ничего не говорит нам о значении х. Значит ли это, что чисел, удовлетворяющих требованию задачи, не существует?

Напротив, это означает, что составленное нами уравнение есть тождество, т. е. что оно верно при любом значении неизвестного х. Действительно, легко убедиться в том, что указанным в задаче свойством обладает каждое двузначное число, у которого цифра единиц на 3 больше цифры десятков:

14 + 27 = 41,  47 + 27 = 74, 
25 + 27 = 52,  58 + 27 = 85, 
36 + 27 = 63,  69 + 27 = 96.

III. Найти трехзначное число, обладающее следующими свойствами:

1. цифра десятков 7;
2. цифра сотен на 4 меньше цифры единиц;
3. если цифры этого числа разместить в обратном порядке, то новое число будет на 396 больше искомого.

Составим уравнение, обозначив цифру единиц через х:

100x + 70 + х - 4 - [100(х - 4) + 70 + x] = 396.

Уравнение это после упрощений приводит к равенству

396 = 396.

Читатели уже знают, как надо толковать подобный результат. Он означает, что каждое трехзначное число, в котором первая цифра на 4 меньше третьей^*, увеличивается на 396, если цифры поставить в обратном порядке.

^* (Цифра десятков роли не играла.)

До сих пор мы рассматривали задачи, имеющие более или менее искусственный, книжный характер; их назначение - помочь приобрести навык в составлении и решении уравнений. Теперь, вооруженные теоретически, займемся несколькими примерами задач практических - из области производства, обихода, военного дела, спорта.