Глава шестая. Зашифрованная переписка

57. Решетка.

Революционер-подпольщик вынужден вести свои записи и переписку с товарищами таким образом, чтобы никто из посторонних не мог понять написанного. Для этого пользуются особым способом письма, называемым "тайнописью" (или "криптографией"). Придуманы разные системы тайнописи; к их услугам прибегают не одни подпольщики, но также дипломаты и военные для сохранения государственных тайн. Расскажем далее об одном из способов ведения секретной переписки, именно о так называемом способе "решетки". Он принадлежит к числу сравнительно простых и тесно связан с арифметикой.

Желающие вести тайную переписку по этому способу запасаются каждый "решеткой", т. е. бумажным квадратиком с прорезанными в нем окошечками.

Образчик решетки вы видите на рис. 41. Окошечки размещены не произвольно, а в определенном порядке, который станет ясен вам из дальнейшего.

Рис. 41. Решетка для тайной переписки. (Сделайте такую из бумаги и прочтите секретную запись рис. 45.)

Пусть требуется послать товарищу такую записку: Собрание делегатов района отмените. Полиция кем-то предупреждена. Антон.

Наложив решетку на листок бумаги, подпольщик пишет сообщение букву за буквой в окошечках решетки.

Так как окошек 16, то сначала помещается только часть записки:

Собрание делегато...

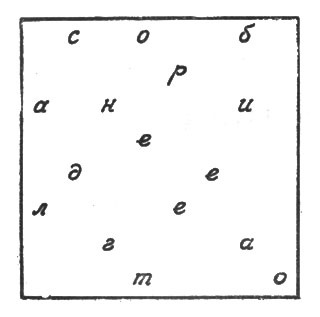
Рис. 42. Сняв решетку, увидим запись

Сняв решетку, мы увидим запись, представленную на рис. 42.

Здесь, разумеется, ничего засекреченного пока нет: каждый легко поймет, в чем дело. Но это только начало; записка в таком виде не останется. Подпольщик поворачивает решетку "по часовой стрелке" на четверть оборота, т. е. располагает ее на том же листке так, что цифра 2, бывшая раньше сбоку, теперь оказывается вверху. При новом положении решетки все ранее написанные буквы заслонены, а в окошечках появляется чистая бумага. В них пишут следующие 16 букв секретного сообщения. Если теперь убрать решетку, получим запись, показанную на рис. 43.

Рис. 43. Пишем затем следующие 16 букв

Такую запись не поймет не только посторонний человек, но и сам писавший, если позабудет текст своего сообщения.

Но записана пока только половина сообщения, именно: Собрание делегатов района отмените. П...

Чтобы писать дальше, надо вновь повернуть решетку на четверть оборота по часовой стрелке. Она закроет все написанное и откроет новые 16 свободных клеток. В них найдут себе место еще несколько слов, и записка приобретет вид рис. 44.

Рис. 44. Надо вновь повернуть решетку

Наконец, делается последний поворот решетки, цифрой 4 вверх, и в открывшиеся 16 чистых квадратиков вписывают окончание записки. Так как остаются три неиспользованные клетки, их заполняют буквами а, б, в, - просто для того, чтобы в записке не оказалось пробелов.

Письмо имеет вид, представленный на рис. 45.

Рис. 45. Секретная записка готова

Попробуйте в нем что-нибудь разобрать! Пусть записка попадет в руки полиции, пусть полицейские сколько угодно подозревают, что в ней скрыто важное сообщение, - догадаться о содержании записки в состоянии только адресат, имеющий в руках точно такую же решетку, как и та, которой пользовался отправитель.

Как же прочтет адресат это секретное письмо? Он наложит свою решетку на текст, обратив ее цифрой 1 вверх, и выпишет те буквы, которые появятся в окошечках. Это будут первые 16 букв сообщения. Затем повернет решетку - и перед ним предстанут следующие 16 букв. После четвертого поворота вся секретная записка будет прочтена.

Вместо квадратной решетки можно пользоваться и прямоугольной, в форме почтовой карточки, с широкими окошечками (рис. 46). В окошечки такой решетки вписывают не отдельные буквы, а части слов, даже целые слова, если они помещаются.

Рис. 46. Решетка в форме почтовой карточки

Не думайте, что запись окажется тогда более разборчивой. Нисколько! Хотя отдельные слоги и слова видны, но перемешаны они в гаком нелепом беспорядке, что секрет достаточно надежно сохранен. Продолговатую решетку кладут сначала одним краем вверх, потом противоположным; после этого переворачивают ее на левую сторону и снова пользуются в двух положениях. В каждом новом положении решетка закрывает все написанное раньше. Если бы возможна была только одна решетка, то способ переписки с ее помощью никуда не годился бы в смысле секретности. В руках полиции, конечно, имелась бы эта единственная решетка, и тайна немедленно раскрывалась бы. Но в том-то и дело, что число различных решеток чрезвычайно велико.

Все решетки, какие можно изготовить для 64-клеточного квадрата, отмечены на рис. 47. Вы можете выбрать для окошечек любые 16 клеток, заботясь лишь о том, чтобы в числе взятых клеток не было двух с одинаковыми номерами. Для той решетки, которой мы пользовались сейчас, взяты были следующие номера клеток:

 2,  4, 5 
    14 
 9, 11, 7 
    16 
 8, 15 
 3, 12 
 10, 6 
 13, 1 

Как видите, ни один номер не повторяется.

Рис. 47. Свыше 4 миллиардов секретных решеток в одном квадрате

Понять систему расположения цифр в квадрате (рис. 47) нетрудно. Он делится поперечными линиями на 4 меньших квадрата, которые обозначим для удобства римскими цифрами I, II, III, IV (рис. 48). В I квадрате клетки перенумерованы в обычном порядке. Квадрат II - тот же квадрат I, только повернутый на четверть оборота вправо.

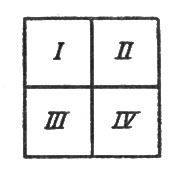
Рис. 48. Схема к рис. 47

Повернув его еще на четверть оборота, получаем квадрат III; при следующей четверти оборота получается квадрат IV.

Подсчитаем теперь математически, сколько может существовать разных решеток. Клетку № 1 можно взять (в качестве окошка) в 4 местах. В каждом случае можно присоединить клетку № 2, взяв ее также в 4 местах. Следовательно, два окошка можно наметить 4 x 4, т. е. 16 способами. Три окошка - 4 x 4 x 4 = 64 способами. Рассуждая таким образом, устанавливаем, что 16 окошек можно набрать 4¹⁶ способами (произведение 16 четверок). Число это превышает 4 миллиарда. Если даже считать наш расчет преувеличенным в несколько раз (так как неудобно пользоваться решетками с примыкающими друг к другу окошечками, и эти случаи надо исключить), то все же остается несколько сотен миллионов решеток, - целый океан! Попробуйте отыскать в нем именно ту, какая требуется.

Если, скажем, группа дешифровальщиков тратит на приготовление решетки и проверку, дает ли она что-либо осмысленное, лишь минуту, то для расшифровки записки могут потребоваться сотни миллионов минут - целые тысячелетия! Впрочем, все это верно лишь в том случае, если расшифровка ведется так сказать "голыми руками". В книге "Занимательная алгебра" того же автора вы можете прочитать о быстродействующих вычислительных машинах. Такие машины могут по определенной программе производить сотни тысяч и даже миллионы вычислений в секунду. Могут они и не только считать. Например, они могут перебирать всевозможные решетки и проверять, дает ли каждая такая решетка осмысленный текст, - нужно лишь составить подходящую программу для такой машины. И если испытание одной решетки на машине требует, скажем, одной тысячной доли секунды, то для перебора сотен миллионов решеток требуются сотни тысяч секунд, т. е. несколько суток. Как видите, в современных условиях сохранение секретности переписки становится затруднительным.

58. Как запомнить решетку? Но предположим, что опасаться рассекречивания с помощью машин не приходится. Скажем, содержание записки должно остаться тайным лишь 2-3 дня, и можно надеяться, что это время недостаточно для перехвата записки, отправки ее в вычислительный центр и дешифровки. Подпольщики решили воспользоваться решеткой. Само собою разумеется, оба участника переписки должны быть начеку, чтобы их решетка не попала в посторонние руки. Лучше всего вовсе не хранить решеток, а вырезать их при получении письма и уничтожать тотчас по прочтении. Но как запомнить расположение окошек? Здесь снова приходит нам на помощь математика. Будем обозначать окошки цифрою 1, прочие же клетки решетки цифрою 0. Тогда первый ряд клеток решетки получит такое обозначение (рис. 49):

01010010

или, отбросив передний нуль, -

1010010.

Рис. 49. Арифметизация секретной решетки

Второй ряд, если отбросить в нем передние нули, обозначится так:

1000.

Прочие ряды получают следующие обозначения:

 10100010 10001000 
 10000    100010 
 1000100  10001. 

Чтобы упростить запись этих чисел, будем считать, что они написаны не по десятичной системе, которою обычно пользуются, а по "двоичной". Это значит, что единица больше соседней, стоящей справа, не в 10 раз, а только в 2 раза. Единица в конце числа означает, как обычно, простую единицу; единица на предпоследнем месте означает двойку; на третьем с конца - четверку; на четвертом - восьмерку; на пятом - 16 и т.д. При таком понимании число 1010010, обозначающее расположение окошек первого ряда, заключает простых единиц

64 + 16 + 2 = 82,

потому что нули указывают на отсутствие единиц данного разряда.

Число 1000 (второй ряд) заменится в десятичной системе числом 8.

Остальные числа нужно будет заменить следующими:

 128 + 32 + 2 = 162 
       16 
       64 + 4 = 68 
      128 + 8 = 136 
       32 + 2 = 34 
       16 + 1 = 17 

Запомнить же числа: 82, 8, 162, 16, 68, 136, 34, 17 не так уж трудно. А зная их, всегда можно получить ту первоначальную группу чисел, из которой они получены и которые прямо указывают расположение окошек в решетке.

Как это делается, покажем на примере первого числа - 82. Разделим его на два, чтобы узнать, сколько в нем двоек; получим 41; остатка нет, - значит, на последнем месте, в разряде простых единиц, должно быть 0. Полученное число двоек 41, делим на 2, чтобы узнать, сколько в нашем числе четверок:

41 : 2 = 20, остаток 1.

Это значит, что в разряде двоек, т. е. на предпоследнем месте, имеется цифра 1.

Далее, делим 20 на 2, чтобы узнать, сколько в нашем числе восьмерок:

20 : 2 = 10.

Остатка нет, - значит, на месте четверок стоит 0.

Делим 10 на 2; получаем 5 без остатка: на месте восьмерок - 0.

От деления 5 на 2 получаем 2 и в остатке 1: в этом разряде стоит цифра 1. Наконец, делим 2 на 2 и узнаем, что в следующем разряде 0, а в последнем разряде 1 (этот разряд соответствует шестидесяти четырем).

Итак, все цифры искомого числа определились:

1010010.

Так как здесь всего 7 цифр, а в каждом ряду решетки 8 клеток, то ясно, что один нуль впереди был опущен, и расположение окошек в первом ряду определяется цифрами:

01010010,

т. е. окошки имеются на 2-м, 4-м и 7-м местах.

Так же восстанавливается расположение окошек и в прочих рядах.

Существует, как было сказано, множество разных систем тайнописи. Мы остановились на решетке потому, что она близко соприкасается с математикой и лишний раз доказывает, как разнообразны те стороны жизни, куда заглядывает эта наука.