Решения головоломок 45-56

45. Все три задачи неразрешимы; счетчик мог безбоязненно обещать за их решения любую премию. Чтобы в этом удостовериться, обратимся к языку алгебры и рассмотрим задачи одну за другой.

Уплата 5 рублей. Предположим, что уплата возможна и что для этого понадобилось х 50-копеечных, у 20-копеечных и z 5-копеечных монет. Имеем уравнение:

50x + 20y + 5z = 500.

Сократив на 5, получаем:

10x + 4y + z = 100.

Кроме того, так как общее число монет, по условию, равно 20, то х, у и z связаны еще и другим уравнением:

x + y + z = 20.

Вычтя это уравнение из первого, получаем:

9x + 3y = 80.

Разделив на 3, приводим уравнение к виду:

3х + у = 26 2/3.

Но 3x, тройное число 50-копеечных монет, есть, конечно, число целое. Число 20-копеечных, у, также целое. Сумма же двух целых чисел не может оказаться числом дробным (26 2/3). Наше предположение о разрешимости этой задачи приводит, как видите, к нелепости. Значит, задача неразрешима.

Подобным же образом читатель убедится в неразрешимости двух других, "удешевленных" задач: с уплатою в 3 и 2 руб. Первая приводит к уравнению

3х + у = 13 1/3,

вторая - к уравнению

3x + у = 6 2/3.

То и другое в целых числах неразрешимо.

Как видите, счетчик нисколько не рисковал, предлагая крупные суммы за решение этих задач: выдать премии никогда не придется.

Другое дело было бы, если бы требовалось уплатить двадцатью монетами названного достоинства не 5, не 3 и не 2 руб., а например 4 руб.: тогда задача легко решалась бы и даже семью различными способами^*.

^* (Вот одно из возможных решений: 6 монет 50-копеечных, 2 монеты 20-копеечные и 12 монет 5-копеечных.)

46. 888 + 88 + 8 + 8 + 8 = 1000.

Имеются и другие решения.

47. Вот два решения:

22 + 2 = 24; 33 - 3 = 24.

48. Приводим три решения:

6 x 6 - 6 = 30; 33 + 3 = 30; 33 - 3 = 30.

49. Недостающие цифры восстанавливаются постепенно, если применить следующий ход рассуждений.

Для удобства пронумеруем строки:

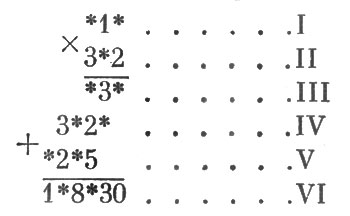
Легко сообразить, что последняя звездочка в III строке цифр есть 0: это ясно из того, что 0 стоит в конце VI строки.

Теперь определяется значение последней звездочки I строки: это - цифра, которая от умножения на 2 дает число, оканчивающееся нулем, а от умножения на 3 - число, оканчивающееся 5 (V ряд). Цифра такая только одна - 5.

Ясно далее, что в конце IV строки стоит цифра 0. (Сравните цифры, стоящие на втором с конца месте в III и VI строках!)

Нетрудно догадаться, что скрывается под звездочкой II строки: 8, потому что только 8 при умножении на число 15 дает результат, оканчивающийся 20 (IV строка).

Наконец, становится ясным значение первой звездочки строки I: это цифра 4, потому что только 4, умноженное на 8, дает результат, начинающийся на 3 (строка IV).

Узнать остальные неизвестные цифры теперь не составляет никакой трудности: достаточно перемножить числа первых двух строк, уже вполне определившиеся.

В конечном итоге получаем такой пример умножения:

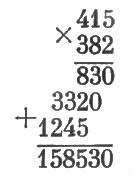
50. Подобным сейчас примененному ходом рассуждений раскрываем значение звездочек и в этом случае.

Получаем:

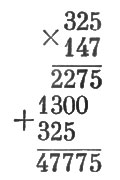
51. Вот искомый случай деления:

52. Чтобы решить эту задачу, надо знать признак делимости на 11. Число делится на 11, если разность между суммою цифр, стоящих на четных местах, и суммою цифр, стоящих на нечетных местах, делится на 11 или равна нулю. Испытаем, для примера, число 23 658 904.

Сумма цифр, стоящих на четных местах:

3 + 5 + 9 + 4 = 21,

сумма цифр, стоящих на нечетных местах:

2 + 6 + 8 + 0 = 16

Разность их (надо вычитать из большего меньшее) равна:

21 - 16 = 5.

Эта разность (5) не делится на 11; значит и взятое число не делится без остатка на 11.

Испытаем другое число: 7344535;

3 + 4 + 3 = 10   7 + 4 + 5 + 5 = 21   21 - 10 = 11.

Так как 11 делится на 11, то и испытуемое число кратно 11.

Теперь легко сообразить, в каком порядке надо писать девять цифр, чтобы получилось число, кратное 11 и удовлетворяющее требованиям задачи.

Вот пример: 352049786.

Испытаем: 3 + 2 + 4 + 7 + 6 = 22, 5 + 0 + 9 + 8 = 22. Разность 22 - 22 = 0; значит, написанное нами число кратно 11.

Наибольшее из всех таких чисел есть; 987652413.

Наименьшее: 102347586.

53. Терпеливый читатель может разыскать девять случаев такого умножения. Вот они:

 12 х 483 = 5796, 48 х 159 = 7632, 

 42 х 138 = 5796, 28 х 157= 4396, 

 18 х 297 = 5346, 4 x 1738 = 6952, 

 27 х 198 = 5346, 4 x 1963 = 7852, 
 
 39 х 186 = 7254, 

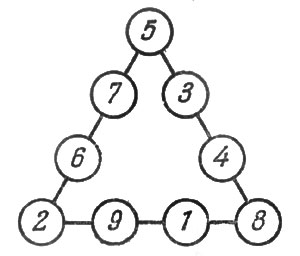
Рис. 38. Решение к задаче 54

54-55. Решения показаны на прилагаемых рисунках 38 и 39. Средние цифры каждого ряда можно переставить и получить таким образом еще ряд решений.

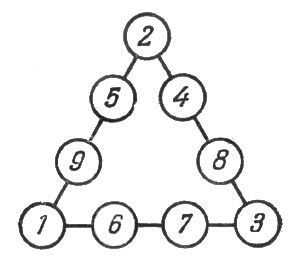
Рис. 39. Решение к задаче 39

56. Чтобы облегчить себе отыскание требуемого расположения чисел, будем руководствоваться следующими соображениями.

Сумма чисел на концах искомой звезды равна 26. сумма же всех чисел звезды 78. Значит, сумма чисел внутреннего шестиугольника равна 78 - 26 = 52.

Рассмотрим затем один из больших треугольников. Сумма чисел каждой его стороны равна 26; сложим числа всех трех сторон - получим 26 x 3 = 78, причем каждое из чисел, стоящих на углах, входит дважды. А так как сумма чисел трех внутренних пар (т. е. сумма чисел внутреннего шестиугольника) должна, мы знаем, равняться 52, то удвоенная сумма чисел на вершинах каждого треугольника равна 78 - 52 = 26; одно кратная же сумма = 13.

Поле поисков теперь заметно сузилось. Мы знаем, например, что ни 12, ни 11 не могут занимать вершины звезды (почему?). Значит, испытания можно начинать с 10, причем сразу определяется, какие два числа должны занимать остальные вершины треугольника: 1 и 2.

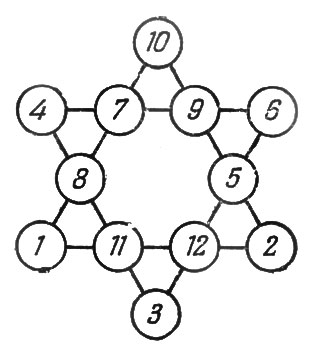
Рис. 40. Решение к задаче 56

Продвигаясь таким путем далее, мы, наконец, разыщем требуемое расположение. Оно показано на рис. 40.