Глава пятая. Числовые головоломки

45. За пять рублей - сто.

Один эстрадный счетчик на своих сеансах делал публике следующее заманчивое предложение:

- Объявляю при свидетелях, что плачу 100 рублей каждому, кто даст мне 5 рублей двадцатью монетами - по 50, 20 и 5 коп. Сто рублей за пять! Кто желает?

Воцарялось молчание.

Публика погружалась в размышление. Карандаши бегали по листкам записных книжек, - но ответного предложения не поступало.

- Публика, я вижу, находит 5 рублей слишком высокой платой за 100 рублей. Извольте, я готов скинуть два рубля и назначаю пониженную цену: 3 рубля двадцатью монетами названного достоинства. Плачу 100 рублей за 3 рубля! Желающие, составляйте очередь!

Но очередь не выстраивалась. Публика явно медлила воспользоваться редким случаем.

- Неужели и 3 рубля дорого? Хорошо, понижаю сумму еще на рубль; уплатите указанными двадцатью монетами всего только 2 рубля, и я немедленно вручу предъявителю сто рублей.

Так как никто не выражал готовности совершить обмен, счетчик продолжал:

- Может быть, у вас нет при себе мелких денег? Не стесняйтесь этим, я поверю в долг. Дайте мне только на бумажке реестрик, сколько монет каждого достоинства вы обязуетесь доставить!

46. Тысяча.

Можете ли вы число 1000 выразить восемью одинаковыми цифрами?

При этом, кроме цифр, разрешается пользоваться также знаками действий.

47. Двадцать четыре.

Очень легко число 24 выразить тремя восьмерками: 8 + 8 + 8. Но можете ли вы сделать то же, пользуясь не восьмерками, а другими тремя одинаковыми цифрами? Задача имеет не одно решение.

48. Тридцать.

Число тридцать легко выразить тремя пятерками: 5 x 5 + 5. Труднее сделать это тремя другими одинаковыми цифрами.

Попробуйте. Может быть, вам удастся отыскать несколько решений?

49. Недостающие цифры.

В этом примере умножения больше половины цифр заменено звездочками.

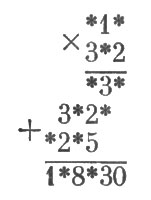
Можете ли вы восстановить недостающие цифры?

50. Какие числа?

Вот еще одна задача такого же рода. Требуется установить, какие числа перемножаются в примере:

51. Что делили?

Восстановите недостающие цифры в таком примере деления:

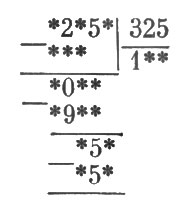
52. Деление на 11.

Напишите какое-нибудь девятизначное число, в котором нет повторяющихся цифр (все цифры разные) и которое делится без остатка на 11.

Напишите наибольшее из таких чисел. Напишите наименьшее из таких чисел.

53. Странные случаи умножения.

Рассмотрите такой случай умножения двух чисел:

48 x 159 = 7632.

Он замечателен тем, что в нем участвуют по одному разу все девять значащих цифр.

Можете ли вы подобрать еще несколько таких примеров? Сколько их, если они вообще существуют?

54. Числовой треугольник.

В кружках этого треугольника (рис. 36) расставьте все девять значащих цифр так, чтобы сумма их на каждой стороне составляла 20.

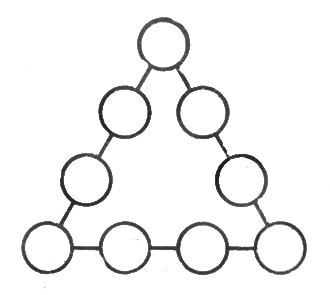
Рис. 36. Расставьте в кружках 9 цифр

55. Еще числовой треугольник.

Все значащие цифры разместить в кружках того же треугольника (рис. 36) так, чтобы сумма их на каждой стороне равнялась 17.

56. Магическая звезда.

Шестиконечная числовая звезда, изображенная на рис. 37 обладает "магическим" свойством: все шесть рядов чисел имеют одну и ту же сумму

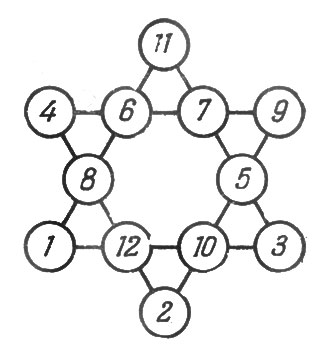
Рис. 37. Шестиконечная числовая звезда

 4 + 6 + 7 + 9 = 26   11 + 6 + 8 + 1 = 26 

 4 + 8 + 12 + 2 = 26  11 + 7 + 5 + 3 = 26 

 9 + 5 + 10 + 2 = 26  1 + 12 + 10 + 3 = 26

Но сумма чисел, расположенных на вершинах звезды, другая:

4 + 11 + 9 + 3 + 2 + 1 = 30.

Не удастся ли вам усовершенствовать эту звезду, расставив числа в кружках так, чтобы не только прямые ряды давали одинаковые суммы (26), но чтобы ту же сумму (26) составляли числа на вершинах звезды?